50 Bài tập về tập hợp (có đáp án năm 2024) - Toán 6

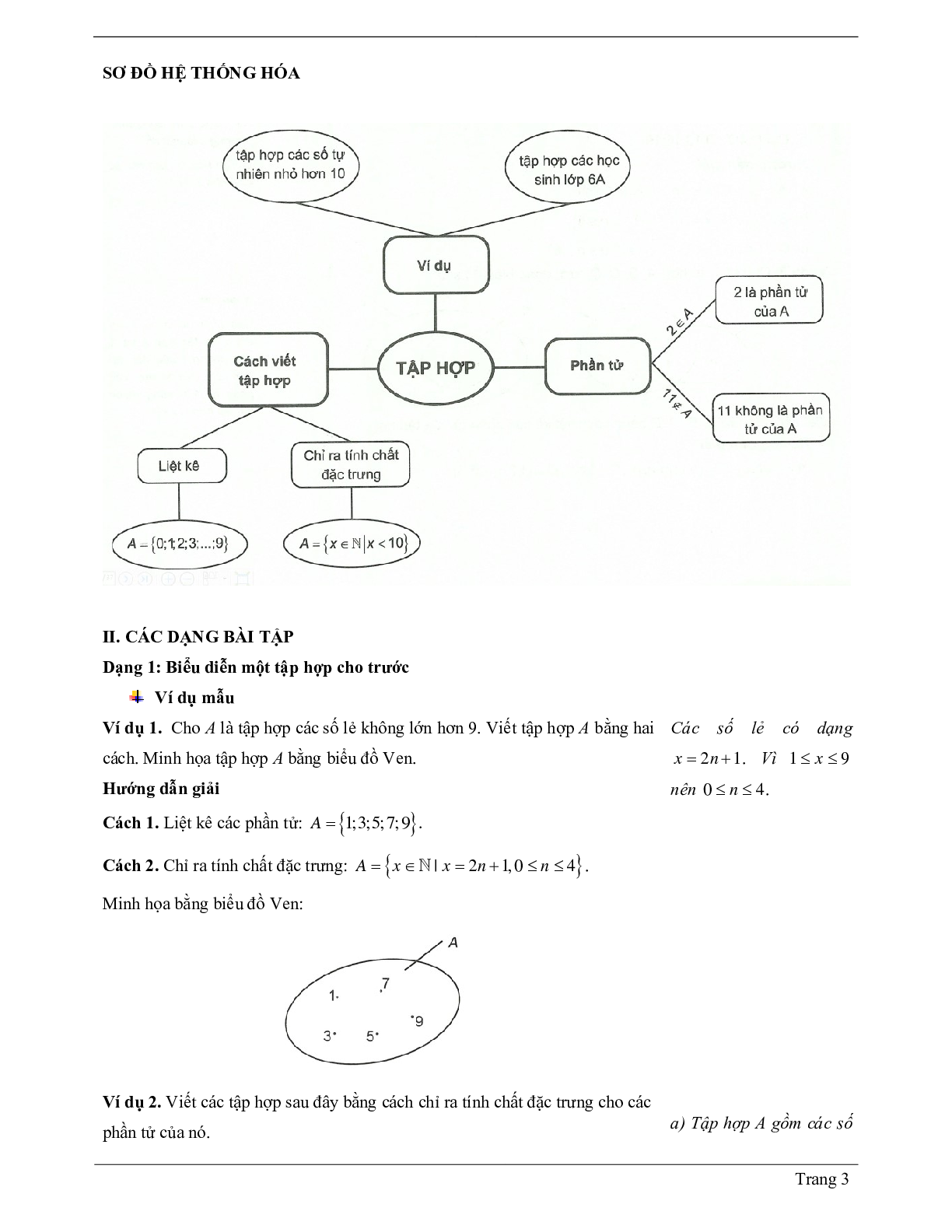
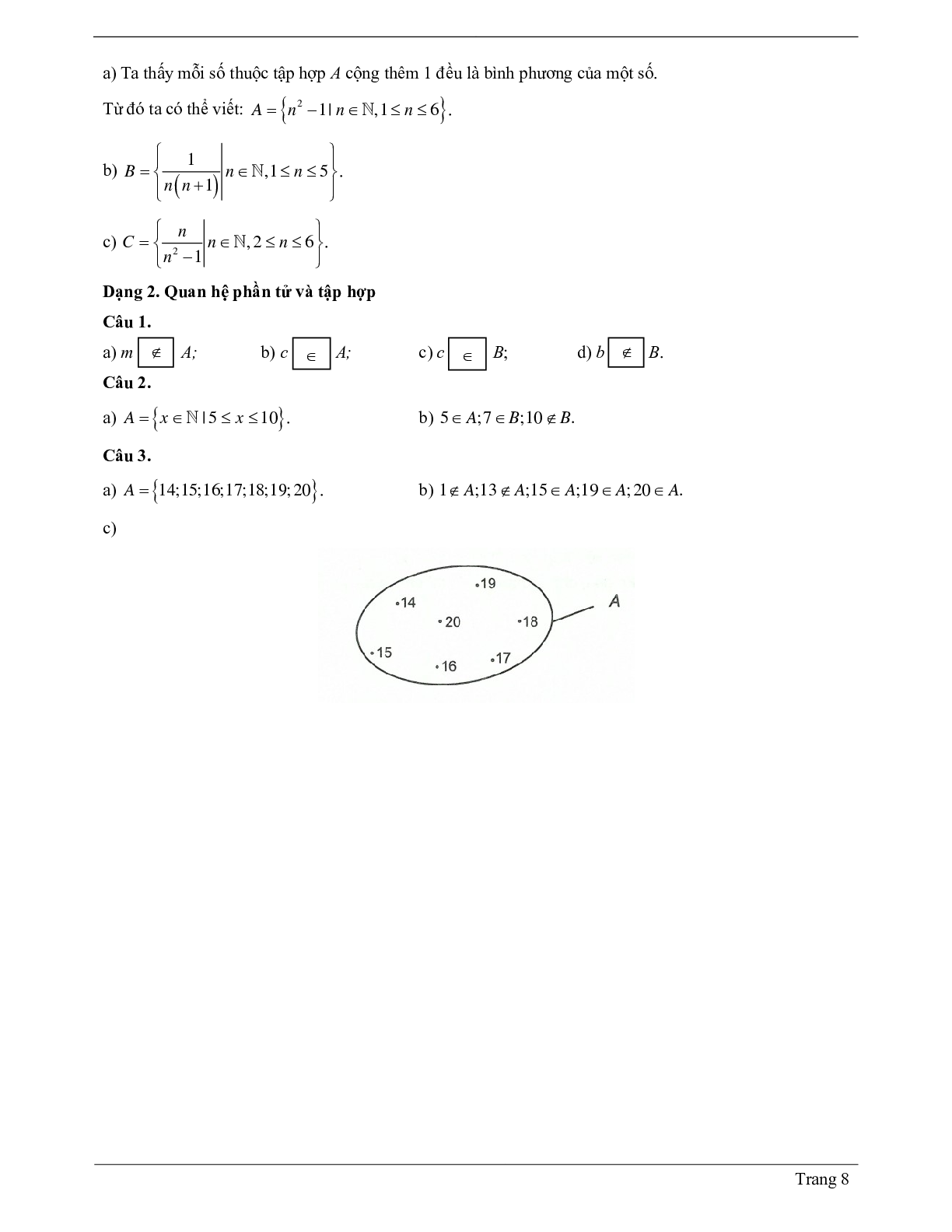
Tập hợp

Kiến thức cần nhớ

1. Tập hợp và phần tử của tập hợp

Tập hợp là một khái niệm cơ bản của toán học (không định nghĩa).

Tập hợp được kí hiệu là các chữ cái in hoa: A, B, C, D, …

Ví dụ 1.

a) Tập hợp các học sinh trong tổ 4 của 6A là: Thắm, Trọng, Xuân, Cương, Bảo, Dũng, Khôi, Huế, Linh.

b) Tập hợp các loại bút bên trong túi bút của bạn Ngọc là: Bút bi, bút chì, bút đánh dấu, bút xóa, bút màu.

Một tập hợp (gọi tắt là tập) bao gồm những đối tượng  nhất định. Các đối tượng ấy được gọi là những phần tử của tập hợp.

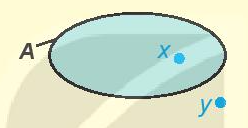
x là một phần tử của tập hợp A. Kí hiệu $x\in A$(đọc là x thuộc A).

y không là một phần tử  của tập hợp A. Kí hiệu $y\notin A$(đọc là y không thuộc A).

Chú ý: Khi x thuộc A, ta còn nói “x nằm trong A”, hay “A chứa x”.

Ví dụ 2. Cho tập hợp M như hình vẽ. Những phần tử nào thuộc tập hợp M, những phần tử nào không thuộc tập hợp M?

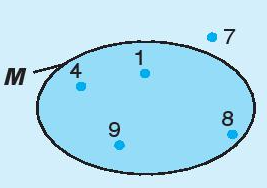
Tập hợp M gồm các phần tử 1; 4; 8; 9.

Ta có 1 là một phần tử của tập hợp M. Kí hiệu $1\in M$.

4 là một phần tử thuộc tập hợp M. Kí hiệu $4\in M$.

8 là một phần tử thuộc tập hợp M. Kí hiệu $8\in M$.

9 là một phần tử thuộc tập hợp M. Kí hiệu $9\in M$.

7 không là phần tử thuộc tập hợp M. Kí hiệu $7\notin M.$

2. Mô tả một tập hợp

2.1. Liệt kê các phần tử của tập hợp

Viết tất cả các phần tử của tập hợp trong dấu {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.

Ví dụ 3. Cho hình vẽ:

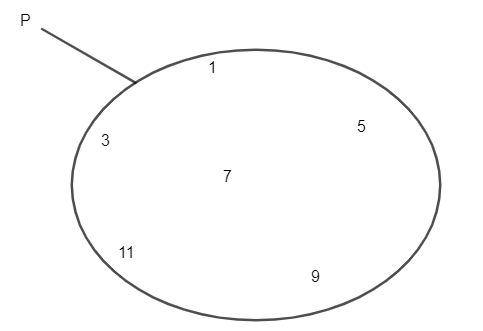
Với tập hợp P gồm các số 1; 3; 5; 7; 9; 11 như hình vẽ.

Theo cách liệt kê, ta viết: P = {1; 3; 5; 7; 9; 11}.

2.1. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp

Gọi x là phần tử của tập hợp, chỉ ra tính chất đặc trưng của phần tử và viết tập hợp đã cho.

Ví dụ 4. Với tập hợp P = {1; 3; 5; 7; 9; 11}.

Ta thấy các phần tử của tập hợp P là các số tự nhiên lẻ và nhỏ hơn 12.

Khi đó, theo cách chỉ ra đặc trưng tập hợp P được viết là:

P = {x | x là số tự nhiên lẻ và nhỏ hơn 12}.

Các dạng bài tập về tập hợp

Dạng 1: Rèn kĩ năng viết tập hợp, viết tập hợp con, sử dụng kí hiệu

Bài 1: Cho tập hợp A là các chữ cái trong cụm từ "Thành phố Hồ Chí Minh"

a. Hãy liệt kê các phần tử của tập hợp A.

b. Điền kí hiệu thích hợp vào ô vuông

b □ A; c □ A; h □ A

Lời giải:

a/ A = {a, c, h, i, m, n, ô, p, t}

b/ 

Lưu ý học sinh: Bài toán trên không phân biệt chữ in hoa và chữ in thường trong cụm từ đã cho, và trong một tập hợp thì mỗi phần tử chỉ xuất hiện một lần

Bài 2: Cho tập hợp các chữ cái X = {A, C, O}

a/ Tìm cụm chữ tạo thành từ các chữ của tập hợp X.

b/ Viết tập hợp X bằng cách chỉ ra các tính chất đặc trưng cho các phần tử của X.

Lời giải:

a/ Chẳng hạn cụm từ "CA CAO" hoặc "CÓ CÁ"

b/ X = {x: x-chữ cái trong cụm chữ "CA CAO"}

Bài 3: Cho các tập hợp

A = {1; 2; 3; 4; 5; 6; 8; 10}; B = {1; 3; 5; 7; 9; 11}

a/ Viết tập hợp C các phần tử thuộc A và không thuộc B.

b/ Viết tập hợp D các phần tử thuộc B và không thuộc A.

c/ Viết tập hợp E các phần tử vừa thuộc A vừa thuộc B.

d/ Viết tập hợp F các phần tử hoặc thuộc A hoặc thuộc B.

Lời giải:

a/ C = {2; 4; 6}

b/ D = {5; 9}

c/ E = {1; 3; 5}

d/ F = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11}

Bài 4: Cho tập hợp A = {1; 2; 3; x; a; b}

a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.

b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.

c/ Tập hợp B = {a, b, c} có phải là tập hợp con của A không?

Lời giải:

a/ {1}; {2}; {a}; {b}; {x}

b/ {1; 2}; {1; a}; {1; b}; {1; 3}; {1; x}; {2; a}; {2; b}; {2; 3}; {2; x}; {3; x}; {3; a}; {3; b}; {x; a}; {x; b}; {a; b}

c/ Tập hợp B không phải là tập hợp con của tập hợp A bởi vì  nhưng 

Bài 5: Cho tập hợp B = {a, b, c}. Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?

Lời giải:

+ Tập hợp con của B không có phần từ nào là  .

+ Các tập hợp con của B có một phần tử là: {a}; {b}; {c}

+ Các tập hợp con của B có hai phần tử là: {a; b}; {a; c}; {b; c}

+ Tập hợp con của B có 3 phần tử chính là B = {a, b, c}

Vậy tập hợp A có tất cả 8 tập hợp con.

Ghi chú. Một tập hợp A bất kỳ luôn có hai tập hợp con đặc biệt. Đó là tập hợp rỗng  và chính tập hợp A. Ta quy ước  là tập hợp con của mọi tập hợp.

Bài 6: Cho A = {1; 3; a; b} ; B = {3; b}

Điền các kí hiệu  thích hợp vào dấu (….)

1 ......A ; 3 ... A ; a....... B ; B ...... A

Lời giải:

1  A ; 3  A ; a  B ; B  A

Bài 7: Cho các tập hợp

; 

Hãy điền dấu hay vào các ô dưới đây

A … N* ; A … B; N …. B

Lời giải:

A  N* ; A  B; N  B

Dạng 2: Các bài tập về xác định số phần tử của một tập hợp

Bài 1: Gọi A là tập hợp các số tự nhiên có 3 chữ số. Hỏi tập hợp A có bao nhiêu phần tử?

Lời giải:

Tập hợp A có (999 – 100) + 1 = 900 phần tử.

Bài 2: Hãy tính số phần tử của các tập hợp sau:

a/ Tập hợp A các số tự nhiên lẻ có 3 chữ số.

b/ Tập hợp B các số 2, 5, 8, 11, …, 296, 299, 302

c/ Tập hợp C các số 7, 11, 15, 19, …, 275 , 279

Lời giải:

a/ Tập hợp A có (999 – 101):2 +1 = 450 phần tử.

b/ Tập hợp B có (302 – 2 ): 3 + 1 = 101 phần tử.

c/ Tập hợp C có (279 – 7 ):4 + 1 = 69 phần tử.

Tổng quát

+ Tập hợp các số chẵn từ số chẵn a đến số chẵn b có (b – a) : 2 + 1 phần tử.

+ Tập hợp các số lẻ từ số lẻ m đến số lẻ n có (n – m) : 2 + 1 phần tử.

+ Tập hợp các số từ số c đến số d là dãy số các đều, khoảng cách giữa hai số liên tiếp của dãy là 3 có (d – c ): 3 + 1 phần tử.

Bài 3: Cha mua cho em một quyển số tay dày 145 trang. Để tiện theo dõi em đánh số trang từ 1 đến 256. Hỏi em đã phải viết bao nhiêu chữ số để đánh hết cuốn sổ tay?

Lời giải:

+ Từ trang 1 đến trang 9, viết 9 chữ số.

+ Từ trang 10 đến trang 99 có 90 trang, viết 90 . 2 = 180 chữ số.

+ Từ trang 100 đến trang 145 có (145 – 100) + 1 = 46 trang, cần viết 46 . 3 = 138 chữ số.

Vậy cần viết 9 + 180 + 138 = 327 số.

Bài 4: Các số tự nhiên từ 1000 đến 10000 có bao nhiêu số có đúng 3 chữ số giống nhau.

Lời giải:

+ Số 10000 là số duy nhất có 5 chữ số, số này có hơn 3 chữ số giống nhau nên không thoả mãn yêu cầu của bài toán.

Vậy số cần tìm chỉ có thể có dạng: , , , với a b là các chữ số.

+ Xét số dạng , chữ số a có 9 cách chọn ( a 0) có 9 cách chọn để b khác a.

Vậy có 9 . 8 = 71 số có dạng .

Lập luận tương tự ta thấy các dạng còn lại đều có 81 số. Suy ta tất cả các số từ 1000 đến 10000 có đúng 3 chữ số giống nhau gồm 81.4 = 324 số.

Bài 5: Có bao nhiêu số có 4 chữ số mà tổng các chữ số bằng 3?

Lời giải:

Vì 3 = 0 + 0 + 3 + 0 = 0 + 1 + 1 + 1 = 1 + 2 + 0 + 0 nên các số có 4 chữ số mà tổng các chữ số bằng 3 là: 3000; 1011; 2001; 1002; 1110; 2100; 1200; 1101; 2010; 1020

Có tất cả 10 số như vậy

Bài 6: Tính nhanh các tổng sau

a, 29 + 132 + 237 + 868 + 763

b, 652 + 327 + 148 + 15 + 73

Lời giải:

a, 29 + 132 + 237 + 868 + 763

= 29 + (132 + 868) + (237 + 763)

= 29 + 1000 + 1000 = 2029

b, 652 + 327 + 148 + 15 + 73

= (652 + 148) + (327 + 73) + 15

= 700 + 400 + 15 = 1115

Bài tập tự luyện 

1. Bài tập vận dụng (có đáp án)

Bài 1: Khi mô tả tập hợp L các chữ cái trong từ NHA TRANG bằng cách liệt kê các phần tử, bạn Nam viết:

L = {N; H; A; T; R; A; N; G}

Theo em, bạn Nam viết đúng hay sai?

Lời giải:

Bạn Nam viết sai vì theo cách mô tả của tập hợp thì mỗi phần tử chỉ được viết một lần nhưng ở đây chữ cái A, N xuất hiện hai lần.

Cách viết đúng là: L = {N; H; A; T; R; G}.

Bài 2: Gọi B là tập hợp các bạn tổ trưởng trong lớp em. Em hãy chỉ ra một bạn thuộc tập B và một bạn không thuộc tập B.

Lời giải:

Giả sử trong lớp em có 4 tổ trưởng có tên là: Mai, Linh, Trang, Nhung

Khi đó: Tập hợp B gồm các bạn: Mai, Linh, Trang, Nhung

+) Bạn Linh thuộc tập hợp B.

+) Bạn Dũng không thuộc tập hợp B.

Bài 3: Viết các tập hợp sau bằng cách liệt kê các phần tử của chúng:

A = {x ∈ ℕ | x < 5};

B = {x ∈ ℕ* | x < 5}.

Lời giải:

Chú ý: kí hiệu ℕ là tập hợp các số tự nhiên và ℕ* là tập hợp các số tự nhiên khác 0.

+) Ta có: A = { x ∈ ℕ | x < 5 }

Trong tập hợp A, ta thấy x ∈ ℕ và x < 5 nên x là các số tự nhiên nhỏ hơn 5, đó là: 0; 1; 2; 3; 4.

Do đó ta viết: A = {0; 1; 2; 3; 4}.

+) Ta có: B = {x ∈ ℕ* | x < 5}

Trong tập hợp B, ta thấy x ∈ ℕ* và x < 5 nên x là các số tự nhiên khác 0 và nhỏ hơn 5, đó là: 1; 2; 3; 4

Do đó ta viết: B = {1; 2; 3; 4}.

Bài 4: Gọi M là tập hợp các số tự nhiên lớn hơn 6 và nhỏ hơn 10.

a) Thay dấu “?” bằng dấu ∈ hoặc ∉: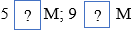 

b) Mô tả tập hợp M bằng hai cách. 

Lời giải:

a) Nhận thấy các số tự nhiên lớn hơn 6 và nhỏ hơn 10 là các số: 7; 8; 9

Nên tập hợp M gồm các số: 7, 8, 9

Do đó: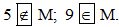

b) Do đó ta có mô tả tập hợp M theo hai cách như sau:

Cách 1: Liệt kê các phần tử của tập hợp

M = {7; 8; 9}.

Cách 2: Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp

M = {x ∈ ℕ | 6 < x < 10}

Bài 5: Cho hai tập hợp:

A = {a; b; c; x; y} và B = {b; d; y; t; u; v}.

Dùng kí hiệu “∈” hoặc “∉” để trả lời các câu hỏi: Mỗi phần tử a, b, x, u thuộc tập nào và không thuộc tập hợp nào?

Lời giải:

+) Tập hợp A có chứa phần tử a, hay a thuộc tập A và ta viết a ∈ A

Tập hợp B không chứa phần tử a, hay a không thuộc tập B và ta viết a ∉ B

+) Tập hợp A có chứa phần tử b, hay b thuộc tập A và ta viết b ∈ A

Tập hợp B có chứa phần tử b, hay b thuộc tập B và ta viết b ∈ B

+) Tập hợp A có chứa phần tử x, hay x thuộc tập A và ta viết x ∈ A

Tập hợp B không chứa phần tử x, hay x không thuộc tập B và ta viết x ∉ B

+) Tập hợp A không chứa phần tử u, hay u không thuộc tập A và ta viết u ∉ A

Tập hợp B có chứa phần tử u, hay u thuộc tập B và ta viết u ∈ B.

Bài 6: Cho tập hợp

U = {x ∈ ℕ | x chia hết cho 3}.

Trong các số 3; 5; 6; 0; 7 số nào thuộc và số nào không thuộc tập hợp U?

Lời giải:

Ta có: U = {x ∈ ℕ | x chia hết cho 3}

Khi đó ta thấy U là tập hợp các số tự nhiên x, sao cho x chia hết cho 3.

Vì x chia hết cho 3 nên các số chia hết cho 3 trong các số đã cho là: 3; 6; 0

Do đó: 3 ∈ U; 5 ∉ U; 6 ∈ U; 0 ∈ U; 7 ∉ U.

Bài 7: Bằng cách liệt kê các phần tử, hãy viết các tập hợp sau:

a) Tập hợp K các số tự nhiên nhỏ hơn 7;

b) Tập hợp D tên các tháng (dương lịch) có 30 ngày;

c) Tập hợp M các chữ cái tiếng Việt trong từ “ĐIỆN BIÊN PHỦ”.

Lời giải:

a) Các số tự nhiên nhỏ hơn 7 là: 0; 1; 2; 3; 4; 5; 6

Do đó tập hợp K gồm các phần tử: 0; 1; 2; 3; 4; 5; 6

Vì vậy, ta viết: K = {0; 1; 2; 3; 4; 5; 6}.

b) Ta đã biết các tháng dương lịch có 30 ngày là: Tháng 4; Tháng 6; Tháng 9; Tháng 11

Do đó tập hợp D gồm các phần tử:  Tháng 4; Tháng 6; Tháng 9; Tháng 11

Vì vậy, ta viết: D = {Tháng 4; Tháng 6; Tháng 9; Tháng 11}.

c) Các chữ cái tiếng Việt trong từ “ĐIỆN BIÊN PHỦ” gồm Đ, I, Ê, N, B, I, Ê, N, P, H, U

Trong các chữ cái trên, chữ I được xuất hiện 2 lần, chữ Ê cũng được xuất hiện 2 lần, chữ N xuất hiện 2 lần nhưng ta chỉ viết trong tập hợp mỗi chữ một lần, ta có tập hợp các chữ cái M = {Đ; I; Ê; N; B; P; H; U}.

Bài 8: Bằng cách nêu dấu hiệu đặc trưng, hãy viết tập hợp A các số tự nhiên nhỏ hơn 10.

Lời giải:

Giả sử n là số tự nhiên nhỏ hơn 10, khi đó n ∈ ℕ và n < 10.

Vì tập hợp A gồm các số tự nhiên nhỏ hơn 10, do đó ta viết được tập hợp A bằng cách nêu dấu hiệu đặc trưng như sau:

A = {n ∈ ℕ | n < 10}

Bài 9: Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quay quanh Mặt Trời gọi là các hành tinh, đó là Thủy Tinh, Kim tinh, Trái Đất, Hỏa tinh, Mộc tinh, Thổ tinh, Thiên Vương tinh và Hải Vương tinh. Gọi S là tập các hành tinh của Hệ Mặt Trời. Hãy viết tập S bằng cách liệt kê các phần tử của S.

Lời giải:

Các hành tinh của hệ Mặt Trời là: Thủy Tinh, Kim tinh, Trái Đất, Hỏa tinh, Mộc tinh, Thổ tinh, Thiên Vương tinh và Hải Vương tinh.

Do đó ta viết tập hợp S bằng cách liệt kê các phần tử của tập hợp như sau:

S = {Thủy Tinh; Kim tinh; Trái Đất; Hỏa tinh; Mộc tinh; Thổ tinh; Thiên Vương tinh; Hải Vương tinh}.

Chú ý: Các phần tử của tập hợp ngăn cách nhau bởi dấu “;”.

2. Bài tập tự luyện có hướng dẫn

Xem thêm các dạng bài tập liên quan khác:

200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)

100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)

500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2023)

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án

300 Bài tập Toán 8 chương 4: Bất phương trình bậc nhất một ẩn (có đáp án năm 2023)