50 Bài tập về phép nhân và phép chia số tự nhiên (có đáp án năm 2024) - Toán 6

Bài tập về phép nhân và phép chia số tự nhiên

Kiến thức cần nhớ

+ Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích.

Kí hiệu: a.b = c (hoặc a x b = c)

Trong đó: a và b là hai thừa số, c là tích.

+ Chú ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …

Ví dụ 1. Tính:

a) 254.35;                                                   b) 86.72.

Lời giải

a)

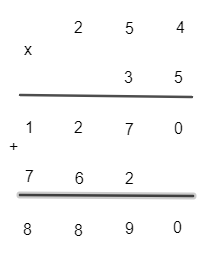
Vậy 254.35 = 8 890.

b)

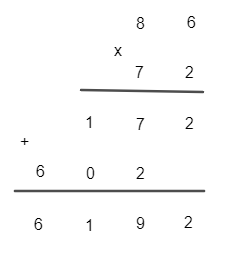
Vậy 86.72 = 6 192.

+ Tính chất của phép nhân:

- Giao hoán: ab = ba.

- Kết hợp: (ab)c = a(bc).

- Phân phối của phép nhân với phép cộng: a(b + c) = ab + ac.

 Ví dụ 2. Thực hiện phép tính:

a) 125.3 542.8;

b) 69.73 + 69.27.

Lời giải

a) 125.3 542.8

= (125.8).3 542

= 1 000. 3 542

= 3 542 000.

b) 69.73 + 69.27

= 69.(73 + 27)

= 69.100

= 6 900.

+ Với hai số tự nhiên a và b đã cho (b khác 0), ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b.q + r, trong đó $0\le r\le b$.

- Nếu r = 0 thì ta có phép chia hết a:b = q; a là số bị chia, b là số chia, q là thương.

- Nếu $r\ne 0$ thì ta có phép chia có dư a:b = q (dư r); a là số bị chia, b là số chia, q là thương, r là số dư.

Ví dụ 3. Thực hiện các phép chia sau:

a) 1 356 : 23;

b) 264 : 12.

Lời giải

a)

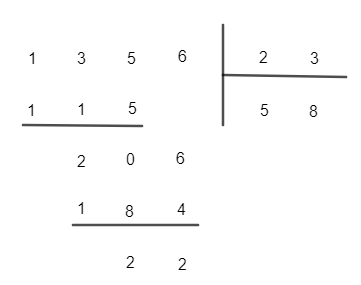
Vậy 1 356 : 23 = 58 (dư 22).

b)

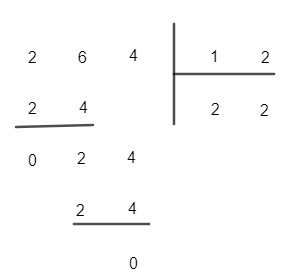
Vậy 264 : 12 = 24 (dư 0)

Các dạng bài tập về phép nhân và phép chia số tự nhiên

Dạng 1. Tìm số chưa biết trong một đẳng thức (phép nhân)

Phương pháp:

+ Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: thừa số = tích : thừa số đã biết

+ Đặc biệt cần chú ý: với mọi $a$$\in$$N$ ta đều có $a.0=0;a.1=a.$

+ Nếu tích hai thừa số bằng 0 thì có ít nhất một thừa số bằng 0.

Ví dụ: 

Tìm $x$, biết $x.5=65$.

Giải:

$x.5=65$

$x=65:5$

$x=13$

Dạng 2. Tìm số tự nhiên có nhiều chữ số khi biết điều kiện xác định các chữ số trong số đó

Phương pháp:

Dựa vào điều kiện xác định các chữ số trong số tự nhiên cần tìm để tìm từng chữ số có mặt trong số tự nhiên đó.

Ví dụ:

Tìm một số tự nhiên có hai chữ số, biết rằng khi thêm 21 vào bên trái số đó thì được một số mới gấp 31 lần số cần tìm.
Giải:

Gọi số cần tìm là $\overline{ab}$ ($0\le a,b\le 9;b\ne 0$), khi viết thêm số 21 vào bên trái số đó ta được số $\overline{21ab}$.

Vì $\overline{21ab}$ gấp 31 lần $\overline{ab}$ nên ta có:

$\begin{array}{l}\overline{ab}\times 31=\overline{21ab}\\ \overline{ab}\times 31=2100+\overline{ab}\\ \overline{ab}\times 31-\overline{ab}\times 1=2100\\ \overline{ab}\times \left(31-1\right)=2100\\ \overline{ab}\times 30=2100\\ \overline{ab}=2100:30\\ \overline{ab}=70\end{array}$

Vậy số cần tìm là $70$.

Dạng 3. Áp dụng các tính chất của phép nhân để tính nhanh

Phương pháp:

- Quan sát, phát hiện các đặc điểm của các thừa số.

- Từ đó, xét xem nên áp dụng tính chất nào (giao hoán, kết hợp, phân phối) để tính một cách nhanh chóng.

Đặc biệt: Viết một số dưới dạng một tích để tính nhanh

Phương pháp:

Bước 1: Căn cứ theo yêu cầu của đề bài, ta có thể viết một số tự nhiên đã cho dưới dạng một tích của hai hay nhiều thừa số.

Bước 2: Sử dụng tính chất giao hoán, kết hợp và phân phối để tính một cách hợp lí.

Dạng 4. So sánh hai tích mà không tính cụ thể giá trị của chúng

Phương pháp:

Nhận xét, phát hiện và sử dụng các đặc điểm của các thừa số trong tổng hoặc tích. Từ đó dựa vào các tính chất phép nhân để rút ra kết luận.

Ví dụ:

So sánh hai tích sau mà không tính giá trị của chúng

$A=2018.2018;B=2017.2019$

Giải:

Ta có:

$\begin{array}{l}A=2018.2018\\ =2018.\left(2017+1\right)\\ =2018.2017+2018.1\\ =2018.2017+2018\\ =2017.2018+2018\\ B=2017.2019\\ =2017.\left(2018+1\right)\\ =2017.2018+2017.1\\ =2017.2018+2017\\ A=2017.2018+2018=2017.2018+2017+1\\ =B+1\\ \Rightarrow A=B+1\end{array}$

Vì $B+1>B$ nên $A>B$.

Bài tập (có đáp án)

1. Bài tập vận dụng

Bài 1:Thực hiện các phép nhân sau:

a) 951 . 23;

b) 47 . 273;

c) 845 . 253;

d) 1 356 . 125.

Lời giải:

a)

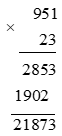
Vậy 951 . 23 = 21 873.

b)

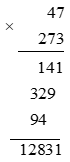
Vậy 47 . 273 = 12 831.

c)

Vậy 845 . 253 = 213 785.

d)

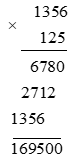
Vậy 1 356 . 125 = 169 500.

Bài 2: Tính nhẩm:

a) 125 . 10

b) 2 021 . 100;

c) 1 991 . 25 . 4

d) 3 025 . 125 . 8.

Lời giải:

a) 125 . 10 = 1 250.

b) 2 021 . 100 = 202 100.

c) 1 991 . 25 . 4 = 1 991 . (25 . 4) = 1 991 . 100 = 199 100.

d) 3 025 . 125 . 8 = 3 025 . (125 . 8) = 3 025 . 1 000 = 3 025 000.

Bài 3: Tính nhẩm:

a) 125 . 101 (Hướng dẫn viết 101 = 100 + 1)

b) 21 . 49 (Hướng dẫn viết 49 = 50 - 1)

Lời giải:

a) 125 . 101 = 125 . (100 + 1) = 125 . 100 + 125 . 1 = 12 500 + 125 = 12 625.

b) 21 . 49 = 21 . (50 - 1) = 21 . 50 - 21 . 1 = 1 050 - 21 = 1 029.

Bài 4: Một trường Trung học cơ sở có 50 phòng học, mỗi phòng có 11 bộ bàn ghế, mỗi bộ bàn ghế có thể xếp cho 4 học sinh ngồi. Trường có thể nhận nhiều nhất bao nhiêu học sinh?

Lời giải:

Mỗi phòng có thể xếp số học sinh ngồi là:

4. 11 = 44 (học sinh)

Trường có thể nhận nhiều nhất số học sinh là:

44 . 50 = 2 200 (học sinh)

Vậy trường có thể nhiều nhất 2 200 học sinh.

Bài 5: Tìm thương và số dư (nếu có) của các phép chia sau:

a) 1 092 : 91

b) 2 059 : 17

Lời giải:

a) 

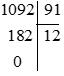
Ta có: 1 092 : 91 = 12

Vậy thương trong phép chia là 12, số dư là 0.

b)

Ta có: 2 059 : 17 = 121 (dư 2)

Vậy thương trong phép chia là 121, số dư là 2.

Bài 6: Tổng điều tra dân số ngày 1 - 4 - 2019, tỉnh Bắc Giang có 1 803 950 người (theo Tổng cục Thống kê). Biết rằng hai lần số dân tỉnh Bắc Giang kém dân số Thanh Hóa 32 228 người. Tính số dân tỉnh Thanh Hóa.

Lời giải:

Hai lần số dân tỉnh Bắc Giang là: 1 803 950 . 2 = 3 607 900 (người)

Vì hai lần số dân tỉnh Bắc Giang kém dân số Thanh Hóa là 32 228 người do đó

Số dân tỉnh Thanh Hóa là:

3 607 900 + 32 228 = 3 640 128 (người)

Vậy số dân tỉnh Thanh Hóa là 3 640 128 người.

Bài 7: Một Trường trung học cơ sở có 997 học sinh tham sự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều có chỗ ngồi?

Lời giải:

Vì 997 : 5 = 199 (dư 2) nên xếp đủ 199 chiếc ghế và còn thừa 2 học sinh và phải dùng thêm 1 chiếc ghế để có chỗ cho 2 học sinh.

Vậy cần dùng ít nhất: 199 + 1 = 200 (ghế băng).

Bài 8: Một nhà máy dùng ô tô chuyển 1 290 kiện hàng tới một cửa hàng. Nếu mỗi chuyến xe chở được 45 kiện thì phải cần ít nhất bao nhiêu chuyến xe để chuyển hết số kiện hàng trên?

Lời giải:

Vì 1 290 : 45 = 28 (dư 30) nên xếp đủ 28 chuyến xe thì còn dư 30 kiện hàng, và phải dùng thêm 1 chuyến xe nữa để chở hết 30 kiện hàng đó.

Vậy, cần ít nhất là: 28 + 1 = 29 (chuyến).