50 Bài tập về phép cộng và phép trừ số tự nhiên (có đáp án năm 2024) - Toán 6

Bài tập về phép cộng và phép trừ số tự nhiên

Kiến thức cần nhớ

1. Phép cộng số tự nhiên

+ Phép cộng hai số tự nhiên a và b cho ta một số tự nhiên gọi là tổng của chúng, kí hiệu là a + b.

Có thể minh họa phép cộng nhờ tia số, chẳng hạn phép cộng 3 + 4 = 7

Ví dụ 1: Tính:

a) 3 + 4;

b) 23 + 37;

c) 78 + 189.

Lời giải

a) 3 + 4 = 7;

b) 23 + 37 = 60;

c) 78 + 189 = 267.

+ Phép cộng số tự nhiên có các tính chất:

-         Giáo hoán: a + b = b + a.

-         Kết hợp: (a + b) + c = a + (b + c).

+ Chú ý: a + 0  = 0 + a = a.

+ Tổng (a + b) + c hay a + (b + c) gọi là tổng của ba số a, b, c và viết gọn là: a + b + c.

Ví dụ 2. Tính:

a) 7 + 12 + 13;

b) 25 + 89 + 75 + 11.

Lời giải

a) 7 + 12 + 13 = 12 + (7 + 13) = 12 + 20 = 32;

b) 25 + 89 + 75 + 11 = (25 + 75) + (89 + 11) = 100 + 100 = 200.

2. Phép trừ số tự nhiên

+ Với hai số tự nhiên a, b đã cho, nếu có số tự nhiên c sao cho a + b = c thì ta có phép trừ

a – b = c. Trong đó, a là số bị trừ, b là số trừ và c là hiệu.

Ví dụ 3. Tính:

a) 725 – 630;

b) 429 – 236.

Lời giải

a) 725 – 630 = 95.

b) 419 – 236 = 183.

Các dạng bài tập về phép cộng và phép trừ số tự nhiên

Dạng 1. Tìm số chưa biết trong một đẳng thức (phép cộng)

Phương pháp:

+ Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: số hạng = tổng - số hạng đã biết

Ví dụ:

Tìm số tự nhiên $x$ biết: $x+17=513$

Giải:

$x+17=513$

$x$        $=513-17$

$x$        $=496$

Vậy $x=496$

Dạng 2. Tìm số chưa biết trong một đẳng thức (phép trừ)

Phương pháp:

+ Muốn tìm một số hạng trong phép cộng hai số, ta lấy tổng trừ số hạng kia.

+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.

+ Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.

Dạng 3. Áp dụng tính chất tổng và hiệu để tính nhanh

Phương pháp:

  Áp dụng một số tính chất sau đây:

+ Tính chất của phép cộng: giao hoán, kết hợp, cộng với số 0.

+ Tổng của hai số không đổi nếu ta thêm vào ở số hạng này và bớt đi ở số hạng kia cùng một số đơn vị.

Ví dụ 1:

- Hiệu của hai số không đổi nếu ta thêm vào một số bị trừ và số trừ cùng một số đơn vị.

Ví dụ 2:

$315-97=\left(315+3\right)-\left(97+3\right)$$=318-100=218$

Dạng 4. So sánh hai tổng mà không tính cụ thể giá trị của chúng

Phương pháp:

Nhận xét, phát hiện và sử dụng các đặc điểm của các số hạng trong tổng. Từ đó dựa vào các tính chất của phép cộng để rút ra kết luận.

Ví dụ:

So sánh hai tổng $1367+5472$ và $5377+1462$ mà không tính giá trị cụ thể của chúng.

Giải:

Đặt $A=1367+5472$ và $B=5377+1462$

$A=1367+5472$

$A=1000+300+67+5000+400+62+10$

$A=5000+1000+400+300+67+62+10$

$B=5377+1462$

$B=5000+300+67+10+1000+400+62$

$B=(5000+1000)+(400+300)+67+62+10$

Như vậy, $A=B$

Bài tập (có đáp án)

1. Bài tập vận dụng

Bài 1: Tính: 865 279 – 45 027

Lời giải:

Vì 865 279 > 45 027 nên phép trừ được thực hiện

Đặt tính rồi tính: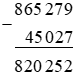 

Vậy: 865 279 - 45 027 = 820 252.

Bài 2: Giải bài toán mở đầu: Mai đi chợ mua cà tím hết 18 nghìn đồng, cà chua hết 21 nghìn đồng và rau cải hết 30 nghìn đồng. Mai đưa cho cô bán hàng tờ 100 nghìn đồng thì được trả lại bao nhiêu tiền?

Lời giải:

Tổng số tiền Mai đã mua là:

18 000 + 21 000 + 30 000 = 69 000 (đồng)

Số tiền Mai được trả lại là:

100 000 - 69 000 = 31 000 (đồng)

Vậy Mai được trả lại 31 000 đồng.

Bài 3: Tính:

a) 63 548 + 19 256;

b) 129 107 - 34 693.

Lời giải:

a) Đặt tính rồi tính: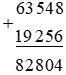 

Vậy 63 548 + 19 256 = 82 804.

b) Đặt tính rồi tính: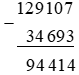  

Vậy 129 107 – 34 693 = 94 414.

Bài 4: Thay "?" bằng số thích hợp:

? + 2 895 = 2 895 + 6 789.

Lời giải:

Áp dụng tính chất giao hoán của phép cộng ta có:

? + 2 895 = 2 895 + ? = 2 895 + 6 789. Suy ra "?" có giá trị 6 789.

Bài 5: Tìm số tự nhiên x thỏa mãn:

a) 7 + x = 362

b) 25 - x = 15

c) x - 56 = 4

Lời giải:

Theo định nghĩa của phép trừ “Nếu có a = b + x thì cũng có a – b = x”

a) 7 + x = 362

x = 362 - 7

x = 355

Vậy x = 355.

b) 25 - x = 15

x = 25 – 15

x = 10

Vậy x = 10.

c) x - 56 = 4

x = 56 + 4

x = 60

Vậy x = 60.

Bài 6: Dân số Việt Nam năm 2019 là 96 462 106 người. Năm 2020, dân số Việt Nam tăng 876 473 người so với năm 2019. Tính dân số Việt Nam năm 2020. (Theo danso.org)

Lời giải:

Do năm 2020, dân số Việt Nam tăng 876 473 người so với năm 2019 nên

Dân số Việt Nam năm 2020 là:

96 462 106 + 876 473 = 97 338 579 (người)

Vậy dân số Việt Nam năm 2020 là 97 338 579 người.

Bài 7: Nhà ga số 1 và nhà ga số 2 của một sân bay có thể tiếp nhận tương ứng khoảng 6 526 300 và 3 514 500 lượt hành khách mỗi năm. Nhờ đưa vào sử dụng nhà ga số 3 mà mỗi năm sân bay này có thể tiếp nhận được khoảng 22 851 200 lượt hành khách. Hãy tính số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm.

Lời giải:

Tổng số lượt hành khách mà nhà ga số 1 và số 2 có thể tiếp nhận mỗi năm là:

6 526 300 + 3 514 500 = 10 040 800 (lượt)

Do tổng số khách cả ba nhà ga mà sân bay có thể tiếp nhận mỗi năm khoảng 22 851 200 lượt khách hàng nên

Số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm là:

22 851 200 - 10 040 800 = 12 810 400 (lượt)

Đáp số: 12 810 400 lượt hành khách.

Bài 8: Tính một cách hợp lí:

a) 285 + 470 + 115 + 230;

b) 571 + 216 + 129 + 124.

Lời giải:

a) 285 + 470 + 115 + 230

= 285 + 115 + 470 + 230 (tính chất giao hoán)

= (285 + 115) + (470 + 230) (tính chất kết hợp) 

= 400 + 700

= 1 100

b) 571 + 216 + 129 + 124

= 571 + 129 + 216 + 124 (tính chất giao hoán)

= (571 + 129) + (216 + 124) (tính chất kết hợp)

= 700 + 340

= 1 040