Phân thức đại số
Lý thuyết
1. Định nghĩa
Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng AB,trong đó A, B là những đa thức và B khác đa thức 0.
Trong đó:
+ A được gọi là tử thức (hay gọi là tử).
+ B được gọi là mẫu thức (hay gọi là mẫu).
Chú ý:
+ Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
+ Số 0, số 1 cũng là một phân thức đại số.
Ví dụ. Ta có các phân thức đại số
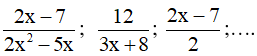
2. Hai phân thức bằng nhau
Hai phân thức AB và CD gọi là bằng nhau nếu A . D = B . C. Ta viết:
AB=CD nếu A . D = B . C.
Ví dụ.
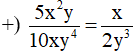vì 5x2y . 2y3 = 10xy4 . x (do cùng bằng 10 x2y4).
vì x . (2x + 4) = 2 . (x2 + 2x) (do cùng bằng 2x2 + 4x).
Các dạng bài tập về phân thức đại số
Dạng 1: Chứng minh hai phân thức bằng nhau
Phương pháp giải
Để chứng minh AB=CD = ta chứng minh AD = BC.
Dạng 2: Tìm giá trị nhỏ nhất (GTNN), giá trị lớn nhất (GTLN) của phân thức
Phương pháp giải
• T = a + [f(x)]2≥𝑎: Giá trị nhỏ nhất của T bằng a khi f(x) = 0.
• T = b – [f(x)]2 ≤𝑏: Giá trị lớn nhất của T bằng b khi f(x) = 0.
Nếu a > 0, T > 0 thì aT nhỏ nhất (hoặc lớn nhất) khi T lớn nhất (hoặc nhỏ nhất).
Dạng 3: Chứng minh đẳng thức
Phương pháp giải
Thực hiện theo ba bước
Bước 1 Lựa chọn 1 trong 3 cách biến đổi thường dùng sau
- Biến đổi vế trái thành vế phải.
- Biến đổi vế phải thành vế trái.
- Biến đổi đồng thời hai vế.
Bước 2 Phân tích tử thức và mẫu thức thành nhân tử.
Bước 3 Rút gọn bằng cách triệt tiêu nhân tử chung và sử dụng định nghĩa hai phân thức bằng nhau nếu cần, từ đó suy ra điều phải chứng minh.
Dạng 4: Tìm đa thức thỏa mãn đẳng thức cho trước
Phương pháp giải
Thực hiện theo hai bước
Bước 1. Phân tích tử thức và mẫu thức thành nhân tử ở hai vế.
Bước 2. Triệt tiêu các nhân tử chung và rút ra đa thức cần tìm.
Dạng 5: Chứng minh đẳng thức có điều kiện
Phương pháp giải
Thực hiện theo hai bước:
Bước 1. Xuất phát từ điều phải chứng minh, áp dụng tính chất hai phân thức bằng nhau (xem phần Tóm tắt lý thuyết).
Bước 2. Thu gọn biểu thức và dựa vào điều kiện đề bài để lập luận.
Xem thêm các dạng Toán hay, chọn lọc khác :
60 Bài tập về Tính chất cơ bản của phân thức (có đáp án năm 2023)
60 Bài tập về Rút gọn phân thức (có đáp án năm 2023)
60 Bài tập về Quy đồng mẫu thức nhiều phân thức (có đáp án năm 2023)
60 Bài tập phép cộng các phân thức đại số (có đáp án năm 2023)
60 Bài tập về phép trừ các phân thức đại số (có đáp án năm 2023)
Tài liệu có 35 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống
