50 Bài tập về dấu hiệu chia hết (có đáp án năm 2024) - Toán 6

Dấu hiệu chia hết

Kiến thức cần nhớ

1. Dấu hiệu chia hết cho 2, cho 5

Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

Ví dụ 1. Cho các số sau: 242; 102; 255; 76; 8 090; 260; 145.

a) Các số chia hết cho 2;

b) Các số chia hết cho 5;

c) Các số chia hết cho cả 2 và 5.

Lời giải

a) Các số chia hết cho 2 là các số có chữ số tận cùng là {0; 2; 4; 6; 8}.

Do đó trong các số trên các số chia hết cho 2 là: 242; 102; 76; 8 090; 260.

b) Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.

Do đó trong các số trên số chia hết cho 5 là: 255; 8 090; 260; 145.

c) Các số chia hết cho cả 2 và 5 là: 8 090; 260.

2. Dấu hiệu chia hết cho 9, cho 3

Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

Chú ý: Các số chia hết cho 9 thì chia hết cho 3 nhưng chia hết cho 3 chưa chắc chia hết cho 9.

Ví dụ 2. Trong các số sau: 1 954; 264; 315; 705; 2 231; 3 771 số nào chia hết cho 3, số nào chia hết cho 9.

Lời giải

+) Ta có: 1 + 9 + 5 + 4 = 19 không chia hết cho 9 cũng không chia hết cho 3 nên 1954 không chia hết cho 3 và 9.

+) Ta có: 2 + 6 + 4 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 264 chia hết cho 3 và không chia hết cho 9.

+) Ta có: 3 + 1 + 5 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 315 vừa chia hết cho 3 vừa chia hết cho 9.

+) Ta có 7 + 0 + 5 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 705 chia hết cho 3 và không chia hết cho 9.

+) Ta có 2 + 2 + 3 + 1 = 8 không chia hết cho 3 cũng không chia hết cho 9 nên 2 231 không chia hết cho 3 cũng không chia hết cho 9.

+) Ta có: 3 + 7 + 7 + 1 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 3771 vừa chia hết cho 3 vừa chia hết cho 9.

Vậy các số chia hết cho 3 là 264; 315; 705; 3 771; các số chia hết cho 9 là 315; 3 771.

Các dạng bài tập về dấu hiệu chia hết

Dạng 1: Nhận biết các số chia hết cho 2, cho 5, cho 3 và cho 9

Bài tập 1.2:

a) Một số chia hết cho cả 2 và 5 thì có chữ số tận cùng là bao nhiêu? Vì sao?

b) Một số chia hết cho 5 nhưng không chia hết cho 2 thì có chữ số tận cùng là bao nhiêu? Vì sao?

c) Một số chia hết cho 2 nhưng không chia hết cho 5 thì có chữ số tận cùng là bao nhiêu? Vì sao?

Bài tập 1.3: Trong các số sau: 123; 104; 500; 345; 1 345; 516; 214; 410; 121

a) Số nào chia hết cho 2?

b) Số nào chia hết cho 5?

c) Số nào chia hết cho 5 nhưng không chia hết cho 2?

d) Số nào chia hết cho cả 2 và 5?

Bài tập 1.4:

a) Một số chia hết cho 9 thì có chia hết cho 3 không? Vì sao?

b) Một số chia hết cho 3 thì có chia hết cho 9 không? Vì sao?

Bài tập 1.5: Trong các số sau: 372; 261; 4 262; 3 772; 5 426; 65 426; 7 371

a) Số nào chia hết cho 3?

b) Số nào chia hết cho 9?

c) Số nào chia hết cho cả 3 và 9?

d) Số nào chia hết cho 3 nhưng không chia hết cho 9?

Bài tập 1.6: Biểu thức nào sau đây có giá trị chia hết cho 3?

a) 120 + 75;

b) 45 . 2 021 – 2 022;

c) 702 – 504 + 2 023 . 15;

d) 64 – 52

Dạng 2: Tìm số tự nhiên thỏa mãn điều kiện cho trước

Bài tập 2.1: Từ các chữ số 0; 2; 5; 7, hãy viết tất cả các số có ba chữ số khác nhau và chia hết cho 2.

Bài tập 2.2: Từ các chữ số 0; 2; 4; 5; 9, hãy viết tất cả các số có hai chữ số khác nhau và chia hết cho 5.

Bài tập 2.3: Số tự nhiên lớn nhất có hai chữ số và chia hết cho 5 là số nào?

Bài tập 2.4: Từ các chữ số 0; 2; 4; 5; 7; 9, hãy viết tất cả các số có ba chữ số khác nhau sao cho các số đó:

a) Chia hết cho 2 nhưng không chia hết cho 5.

b) Chia hết cho cả 2 và 5.

Bài tập 2.5: Tìm tập hợp các số x thỏa mãn:

a) x chia hết cho 2 và 467 < x ≤ 480.

b) x chia hết cho 5 và 467 < x ≤ 480.

c) x vừa chia hết cho 2, vừa chia hết cho 5 và 467 < x ≤ 480.

Bài tập 2.6: Tìm tập hợp các số m thỏa mãn:

a) m chia hết cho 9 và 58 < m < 82.

b) m chia hết cho 3 và 15 ≤ m < 33.

Bài tập 2.7: Điền chữ số vào dấu  để:

a)  chia hết cho 3;

b)  chia hết cho 9;

c)  chia hết cho cả 3 và 5;

Dạng 3: Toán có lời văn

Bài tập 3.1: Một công ty có một số công nhân hưởng mức lương 360 nghìn đồng / tháng; số khác hưởng mức 495 nghìn đồng / tháng; số còn lại hưởng mức 672 nghìn đồng / tháng. Sau khi phát lương tháng 7 cho công nhân, cô kế toán tính tổng số tiền đã phát thì được kết quả là 273 815 nghìn đồng. Hỏi cô kế toán tính đúng hay sai? Tại sao?

Bài tập 3.2: Hai bạn An và Khang đi mua 18 gói bánh và 12 gói kẹo để đến lớp liên hoan. An đưa cho cô bán hàng 4 tờ tiền loại 50 000 đồng và được trả lại 72 000 đồng. Khang nói: “Thưa cô, cô tính nhầm rồi!” Em hãy cho biết Khang nói đúng hay sai? Vì sao?

Đáp án các bài tập:

Dạng 1:

Bài tập 1.1:

a) Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2. Vậy trong các số đã cho, số chia hết cho 2 là: 22; 18; 2 022; 7 980.

b) Số chia hết cho 5 thì chữ số tận cùng phải là 0 hoặc 5. Vậy các số chia hết cho 5 là: 15; 7 980.

c) Dựa vào câu a) và câu b), số chia hết cho cả 2 và 5 là: 7 980.

d) Các số 15; 27; 18; 2 022; 7 980 chia hết cho 3 vì tổng các chữ số của mỗi số đó đều chia hết cho 3.

Các số còn lại không chia hết cho 3 vì tổng các chữ số của mỗi số đó không chia hết cho 3.

e) Các số 27 và 18 chia hết cho 9 vì tổng các chữ số của mỗi số đó chia hết cho 9.

Các số còn lại không chia hết cho 9 vì tổng các chữ số của chúng không chia hết cho 9.

Bài tập 1.2:

a) Số chia hết cho 5 thì tận cùng của nó phải là chữ số 0 hoặc 5. Nhưng nếu tận cùng là 5 thì lại không chia hết cho 2. Vậy để một số chia hết cho cả 2 và 5 thì chữ số tận cùng của nó phải là chữ số 0.

b) Số chia hết cho 5 nhưng không chia hết cho 2 thì chữ số tận cùng của nó phải là chữ số 5, vì nếu tận cùng là 0 thì nó sẽ chia hết cho 2.

c) Số chia hết cho 2 thì tận cùng phải là 0; 2; 4; 6; 8. Tuy nhiên, nếu tận cùng là 0 thì nó sẽ chia hết cho 5. Vậy để một số chia hết cho 2 nhưng không chia hết cho 5 thì chữ số tận cùng của nó phải là 2; 4; 6 hoặc 8.

Bài tập 1.3:

a) Các số 104; 500; 516; 214 và 410 chia hết cho 2.

b) Các số 500; 345; 1 345; 410 chia hết cho 5.

c) Các số 345; 1 345 chia hết cho 5 nhưng không chia hết cho 2.

d) Các số 500; 410 chia hết cho cả 2 và 5.

Bài tập 1.4:

a) Một số chia hết cho 9 thì chia hết cho 3 vì 9 chia hết cho 3.

b) Một số chia hết cho 3 thì chưa chắc chia hết cho 9. Ví dụ: 15 chia hết cho 3 nhưng không chia hết cho 9.

Bài tập 1.5:

a) Ta có:

3 + 7 + 2 = 12 chia hết cho 3 nên 372 chia hết cho 3;

2 + 6 + 1 = 9 chia hết cho 3 nên 261 chia hết cho 3;

4 + 2 + 6 + 2 = 14 không chia hết cho 3 nên 4 262 không chia hết cho 3;

3 + 7 + 7 + 2 = 19 không chia hết cho 3 nên 3 772 không chia hết cho 3;

5 + 4 + 2 + 6 = 17 không chia hết cho 3 nên 5 426 không chia hết cho 3;

6 + 5 + 4 + 2 + 6 = 23 không chia hết cho 3 nên 65 426 không chia hết cho 3;

7 + 3 + 7 + 1 = 18 chia hết cho 3 nên 7 371 chia hết cho 3.

Vậy các số 372; 261 và 7 371 chia hết cho 3.

b) Các số 261 và 7 371 chia hết cho 9 vì tổng các chữ số của mỗi số đó chia hết cho 9.

c) Các số chia hết cho 9 thì chia hết cho 3. Vậy các số chia hết cho 9 thì chia hết cho cả 3 và 9, đó là các số 261 và 7 371.

d) Số 372 chia hết cho 3 nhưng không chia hết cho 9.

Bài tập 1.6:

a) Ta có:

1 + 2 + 0 = 3 chia hết cho 3 nên 120 chia hết cho 3;

7 + 5 = 12 chia hết cho 3 nên 75 chia hết cho 3.

Do đó 120 + 75 chia hết cho 5.

b) Ta có:

45 chia hết cho 3 nên 45 . 2 021 chia hết cho 3;

Vì 2 + 0 + 2 + 2 = 6 chia hết cho 3 nên 2 022 chia hết cho 3.

Do đó, 45 . 2 021 – 2 022 chia hết cho 3.

c) Ta có:

7 + 0 + 2 = 9 chia hết cho 3 nên 702 chia hết cho 3;

5 + 0 + 4 = 9 chia hết cho 3 nên 504 chia hết cho 3;

Vì 15 chia hết cho 3 nên 2 023 . 15 chia hết cho 3.

Do đó, 702 – 504 + 2 023 . 15 chia hết cho 3

d) Ta có:

6 chia hết cho 3 nên 64 chia hết cho 3. (Vì 64 là tích của 4 số 6).

52 = 25 không chia hết cho 3.

Do đó 64 – 52 không chia hết cho 3.

Dạng 2:

Bài tập 2.1: Số cần viết có 3 chữ số khác nhau lấy từ 0; 2; 5; 7 và tận cùng là 0 hoặc 2.

• 0 là chữ số tận cùng: 250; 270; 520; 570; 720; 750;

• 2 là chữ số tận cùng: 502; 572; 702; 752.

Vậy các số cần tìm là: 250; 270; 520; 570; 720; 750; 502; 572; 702; 752.

Bài tập 2.2: Số cần viết có hai chữ số khác nhau lấy từ 0; 2; 4; 5; 9 và tận cùng là 0 hoặc 5.

• 0 là chữ số tận cùng: 20; 40; 50; 90;

• 5 là chữ số tận cùng: 25; 45; 95.

Vậy các số cần tìm là: 20; 40; 50; 90; 25; 45; 95.

Bài tập 2.3: Số tự nhiên lớn nhất có hai chữ số và chia hết cho 5 là 95.

Bài tập 2.4:

a) Số cần tìm tận cùng là 2 hoặc 4:

• 2 là chữ số tận cùng: 402; 452; 472; 492; 502; 542; 572; 592; 702; 742; 752; 792; 902; 942; 952; 972;

• 4 là chữ số tận cùng: 204; 254; 274; 294; 504; 524; 574; 594; 704; 724; 754; 794; 904; 924; 954; 974.

b) Số cần tìm tận cùng là 0, đó là các số: 240; 250; 270; 290; 420; 450; 470; 490; 520; 540; 570; 590; 720; 740; 750; 790; 920; 940; 950; 970.

Bài tập 2.5:

a) {468; 470; 472; 474; 476; 478; 480}

b) {470; 475; 480}

c) {470; 480}

Bài tập 2.6:

a) {63; 72; 81}

b) {15; 18; 21; 24; 27; 30}

Bài tập 2.7:

a) Để  chia hết cho 3 thì tổng các chữ số của nó phải chia hết cho 3.

Ta có: 6 + * + 7 = 13 + *

Thay * lần lượt bởi các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9, ta thấy khi * bằng 2; 5 hoặc 8 thì 13 + * chia hết cho 3.

Vậy * là 2 hoặc 5 hoặc 8 thì  chia hết cho 3.

b) Để  chia hết cho 9 thì tổng các chữ số của nó phải chia hết cho 9.

Ta có: 1 + * + 8 = 9 + *

Thay * lần lượt bởi các chữ số từ 0 đến 9, ta thấy khi * bằng 0 hoặc 9 thì 9 + * chia hết cho 9.

Vậy * là 0 hoặc 9 thì  chia hết cho 9.

c) Để  chia hết cho 5 thì * (chữ số tận cùng) phải là 0 hoặc 5.

Nếu * = 0 thì ta được số 210. Đây là một số chia hết cho 3 vì tổng các chữ số của nó là 2 + 1 + 0 = 3 chia hết cho 3.

Nếu * = 5 thì ta được số 215. Số này không chia hết cho 3 vì tổng các chữ số của nó là 2 + 1 + 5 = 8 không chia hết cho 3. Ta loại trường hợp này.

Vậy khi * = 0 thì  chia hết cho cả 3 và 5.

Dạng 3:

Bài tập 3.1: Gọi a, b, c lần lượt là số công nhân hưởng mức lương 360 nghìn đồng / tháng, 495 nghìn đồng / tháng và 672 nghìn đồng / tháng.

Khi đó, tổng số tiền phải phát cho công nhân được tính bởi biểu thức sau:

A = a . 360 + b . 495 + c . 672

Vì 3 + 6 + 0 = 9 chia hết cho 3 nên 360 chia hết cho 3. Do đó: a . 360 chia hết cho 3.

Vì 4 + 9 + 5 = 18 chia hết cho 3 nên 495 chia hết cho 3. Do đó: b . 495 chia hết cho 3.

Vì 6 + 7 + 2 = 15 chia hết cho 3 nên 672 chia hết cho 3. Do đó, c . 672 chia hết cho 3.

Vậy A = a . 360 + b . 495 + c . 672 chia hết cho 3. Tức là tổng số tiền phát cho công nhân là một số chia hết cho 3.

Kết quả mà cô kế toán đưa ra là: 273 815.

Ta có: 2 + 7 + 3 + 8 + 1 + 5 = 26 không chia hết cho 3 nên 273 815 không chia hết cho 3.

Vậy cô kế toán đã tính sai vì kết quả mà cô đưa ra không chia hết cho 3.

Bài tập 3.2: Gọi a và b lần lượt là giá tiền của gói bánh và gói kẹo.

Khi đó, số tiền để mua 18 gói bánh và 12 gói kẹo là: 18a + 12b

Vì 18 và 12 đều chia hết cho 3 nên 18a và 12b cũng chia hết cho 3. Do đó: 18a + 12b chia hết cho 3. Vậy số tiền để mua bánh và kẹo là một số chia hết cho 3.

An đưa cho cô bán hàng 4 tờ tiền loại 50 000 đồng, nếu cô trả lại cho An 72 000 đồng thì có nghĩa là số tiền để mua bánh và kẹo là: 4 . 50 000 – 72 000 = 128 000 (đồng).

Ta có: 1 + 2 + 8 + 0 + 0 + 0 = 11 không chia hết cho 3 nên 128 000 không chia hết cho 3.

Do đó, cô bán hàng đã tính sai. Tức là Khang đã nói đúng.

Bài tập (có đáp án)

Bài tập vận dụng

Bài 1: Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5? 

324; 248; 2 020; 2025.

Lời giải:

+) Vì các số 324; 248; 2 020 có chữ số tận cùng lần lượt là 4; 8; 0 nên 324; 248; 2 020 chia hết cho 2

+) Vì các số 2 020; 2025 có chữ số tận cùng lần lượt là 0 và 5 nên 2 020; 2025 chia hết cho 5.

Bài 2: Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9?

450 ; 123 ; 2 019 ; 2 025.

Lời giải:

+) Xét số 450 có tổng các chữ số 4 + 5 + 0 = 9, vì 9 ⁝ 3 và 9 ⁝ 9 nên 450 ⁝ 3 và 450 ⁝ 9.

+) Xét số 123 có tổng các chữ số 1 + 2 + 3 = 6, vì 6 ⁝ 3 và 69 nên 123 ⁝ 3 và 1239

+) Xét số 2 019 có tổng các chữ số 2 + 0 + 1 + 9 = 12, vì 12 ⁝ 3 và 129 nên 2 019 ⁝ 3 và

2 0199

+) Xét số 2 025 có tổng các chữ số 2 + 0 + 2 + 5 = 9, vì 9 ⁝ 3 và 9 ⁝ 9 nên 2 025 ⁝ 3 và 20 25 ⁝ 9

2 025 ⁝ 9.

Vậy các số chia hết cho 3 là: 450; 123; 2 019; 2 025

        các số chia hết cho 9 là: 450; 2 025.

Bài 3: Khối lớp 6 của một trường có 290 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?

Lời giải:

Tổng các chữ số của số 290 là 2 + 9 + 0 =11 không chia hết cho 9 nên 290 không chia hết cho 9. Do đó mà cô không thể chia đều 290 học sinh đi dã ngoại thành 9 nhóm.

Vậy không thể chia đều số học sinh của khối 6 thành 9 nhóm.

Bài 4: Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Hỏi có đội nào không đủ 9 học sinh hay không?

Lời giải:

Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.

Bài 5: Thay dấu * bởi một chữ số để số :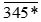

a) Chia hết cho 2

b) Chia hết cho 3

c) Chia hết cho 5

d) Chia hết cho 9.

Lời giải:

Điều kiện * ∈ N, 0 ≤ * ≤ 9

a) Số 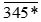chia hết cho 2 thì nó phải có tận cùng là chữ số chẵn nên * ∈ {0;2;4;6;8}

Vậy có thể thay * bằng các chữ số: 0; 2; 4; 6; 8

b) Số 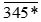 chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3.

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 3.

Mà 12 chia hết cho 3 nên * cũng phải chia hết cho 3 nên * ∈ {0;3;6;9}

Vậy có thể thay * bằng các chữ số: 0; 3; 6; 9

c) Số 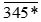 chia hết cho 5 thì nó phải có tận cùng là 0 hoặc 5 nên * ∈ {0;5}

Vậy có thể thay * bằng các chữ số: 0 ; 5

d) Số 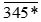chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 9 nên * ∈ {6}

Vậy có thể thay * bằng chữ số 6.

Bài 6: Dùng 3 chữ số 3, 0, 4 hãy viết các số tự nhiên có ba chữ số khác nhau và thỏa mãn một trong hai điều kiện:

a) Các số đó chia hết cho 2

b) Các số đó chia hết cho 5

Lời giải:

a) Vì số cần tìm là số tự nhiên chia hết cho 2 nên số cần tìm có chữ số tận cùng là 0 hoặc 4. 

+) Với chữ số tận cùng là 0 và có ba chữ số khác nhau ta được số cần tìm là: 340; 430.

+) Với chữ số tận cùng là 4, chữ số 0 không thể đứng đầu nên số 0 ở hàng chục và số tự nhiên có ba chữ số khác nhau nên ta được số cần tìm là: 304

Vậy các số chia hết cho 2 là:  304; 340; 430.

b) Vì số cần tìm là số tự nhiên chia hết cho 5 nên số cần tìm có chữ số tận cùng là 0. 

Vì số tự nhiên có ba chữ số khác nhau nên ta viết được các số: 340; 430

Vậy các số chia hết cho 5:  340; 430.

Bài 7: Từ các chữ số 5, 0, 4, 2 viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.

Lời giải:

5 + 4 + 0 = 9 

4 + 2 + 0 = 6

Bộ ba chữ số khác nhau có tổng của chúng chia hết cho 3 là: (5; 4; 0) và (4; 2; 0)

+) Với bộ ba chữ số (5; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 504; 540; 405; 450

+) Với bộ ba chữ số (2; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 420; 402; 240; 204.

Vậy các số cần tìm là: 504; 540; 405; 450; 420; 402; 240; 204.