Khối đa diện lồi và khối đa diện đều
Kiến thức cần nhớ
I. Khối đa diện lồi.
Khối đa diện lồi (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
Ví dụ 1. Các khối chóp tam giác, tứ giác, các khối lăng trụ tam giác, khối lăng trụ tứ giác… đều là những khối đa diện đều.
- Người ta chứng minh được rằng, một khối đa diện là khối đa diện lồi khi và chỉ khi miềm trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó.
II. Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
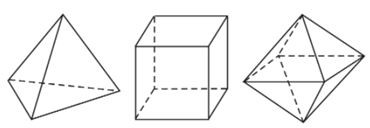
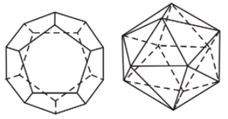
Bảng tóm tắt của năm loại khối đa diện đều.

Ví dụ 2. Chứng minh rằng nếu khối đa diện có các mặt là những tam giác thì tổng các mặt của nó phải là một số chẵn.
Lời giải:
Gọi số cạnh và số mặt của đa diện lần lượt là c và m .
Vì mỗi mặt có ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt nên ta có số cạnh của đa diện là c=3m2⇒3m=2c.
Do đó, 3m chia hết cho 2 mà 3 không chia hết cho 2 nên m phải chia hết cho 2, nghĩa là m là số chẵn.
Vậy nếu khối đa diện có các mặt là những tam giác thì tổng các mặt của nó phải là một số chẵn.
Các dang bài tập về khối đa diện lồi và khối đa diện đều
Dạng 1: Nhận diện đa diện lồi, đa diện đều.
Dạng 2: Các đặc điểm của khối đa diện đều.
Bài tập tự luyện
1 Bài tập vận dụng
Câu 1: Khối bát diện là khối đa diện đều thuộc loại nào?
Lời giải:
Khối bát diện là khối đa diện đều thuộc loại (3;4)
Câu 2: Khối 12 mặt đều là khối đa diện đều thuộc loại nào?
Lời giải:
Khối 12 mặt đều là khối đa diện đều thuộc loại (5; 3)
Câu 3: Điền vào chỗ trống cụm từ nào cho dưới đây để được một mệnh đề đúng?
“Tồn tại hình đa diện đều mà các mặt của nó là những….”
Lời giải:
“Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều. Đó chính là khối mười hai mặt đều.
Câu 4: Trong các mệnh đề sau, mệnh đề nào sai?
A. Tồn tại hình đa diện đều mà các mặt của nó là những tam giác đều
B. Tồn tại hình đa diện đều mà các mặt của nó là những hình vuông
C. Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều
D. Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều
Lời giải:
Trong các mệnh đề sau, mệnh đề nào sai?
* Tồn tại hình đa diện đều mà các mặt của nó là những tam giác đều. Đó là khối hai mươi mặt đều.
* Tồn tại hình đa diện đều mà các mặt của nó là những hình vuông. Đó là hình lập phương.
* Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều. Đó là khối mười hai mặt đều.
Mệnh đề: Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều là sai.
Câu 5: Trong các hình đa diện đều sau, hình nào có số đỉnh lớn hơn số mặt?
Lời giải:
Dễ thấy A, B sai. Hình 12 mặt đều thuộc loại (5 ;3) nên 5m = 3d, nên d > m
Câu 6: Trong các hình đa diện đều sau, hình nào có số đỉnh nhỏ hơn số mặt?
Hình tứ diện đều
Hình 12 mặt đều
Hình lập phương
Hình 20 mặt đều
Lời giải:
Hình tứ diện đều có 4 đỉnh và 4 mặt
Hình lập phương có 8 đỉnh và 6 mặt
Hình 12 mặt đều có 12 mặt và 20 đỉnh
Hình 20 mặt đều có 20 mặt và 12 đỉnh
Chọn D
Câu 7: Các mặt của khối 12 mặt đều là những đa giác nào?
Lời giải:
Các mặt của khối 12 mặt đều là những ngũ giác đều
Câu 8: Các mặt của khối 20 mặt đều là những đa giác nào?
Lời giải:
Các mặt của khối 20 mặt đều là những tam giác đều
Câu 9: Khối bát diện đều có bao nhiêu đỉnh?
Lời giải:
Khối bát diện đều có 6 đỉnh.
Câu 10: Khối 20 mặt đều có bao nhiêu đỉnh?
Lời giải:
Khối 20 mặt đều thuộc loại (3 ;5), nên ta có 3.20 = 5d, suy ra d = 12
2 Bài tập tự luyện có hướng dẫn
Xem thêm các dạng bài tập liên quan khác:
60 Bài tập về khối đa diện lồi và khối đa diện đều ( có đáp án năm 2023 )
60 Bài tập về mặt cầu (có đáp án năm 2023)
60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023)
60 Bài tập về phương trình mặt phẳng (có đáp án năm 2023)
60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2023)




