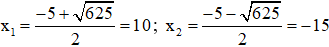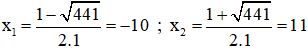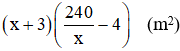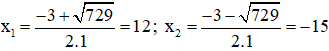50 Bài tập Giải bài toán bằng cách lập phương trình (có đáp án năm 2024) - Toán 9

Giải bài toán bằng cách lập phương trình

Kiến thức cần nhớ 

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

- Chọn ẩn và đặt điều kiện thích hợp cho chúng

- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình nói trên. 

Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận.

Bài tập tự luyện 

Bài 1: Trong lúc học nhóm, bạn Hùng yêu cầu bạn Minh và bạn Lan mỗi người chọn một số sao cho hai số này hơn kém nhau là 5 và tích của chúng phải bằng 150. Vậy hai bạn Minh và Lan phải chọn những số nào?

Lời giải

Gọi x là số mà một bạn chọn

⇒ số còn lại là x + 5.

⇒ tích của hai số là x(x+5).

Theo đề bài ta có phương trình:

     x(x+ 5) = 150

⇔ x² + 5x = 150

⇔ x² + 5x – 150 = 0 (*)

Phương trình (*) có: a = 1; b = 5; c = -150

⇒ Δ = 5² – 4.1.(-150) = 625 > 0

⇒ (*) có hai nghiệm

Vậy hai số mà Minh và Lan phải chọn là 10 và 15.

Hoặc hai số mà hai bạn chọn là -10 và –15.

Bài 2: Bác Thời vay 2 000 000 đồng của ngân hàng để làm kinh tế gia đình trong thời hạn một năm. Lẽ ra cuối năm bác phải trả cả vốn lẫn lãi. Song bác đã được ngân hàng cho kéo dài thời hạn thêm một năm nữa, số lãi của năm đầu được gộp vào với vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết hai năm bác phải trả tất cả là 2 420 000 đồng. Hỏi lãi suất cho vay là bao nhiêu phần trăm trong một năm?

Lời giải

Gọi lãi suất cho vay là : x (x > 0).

Lãi suất sau năm đầu tiên là : 2 000 000.x

Số tiền bác phải trả sau năm đầu tiên là :

2 000 000 + 2 000 000.x = 2 000 000.(1 + x)

Số tiền trên được tính là vốn của năm thứ hai.

Số tiền lãi của năm thứ hai là : 2 000 000.(1 + x).x

Số tiền vốn và lãi phải trả sau năm thứ hai là:

2 000 000.(1 + x) + 2 000 000.(1 + x). x

= 2 000 000 + 2 000 000.x + 2 000 000.x + 2 000 000$x^2$

= 2 000 000.$\left(1+x+x+x^2\right)$

= 2 000 000.$\left(1+2x+x^2\right)$

= 2 000 000.(1 + x)²

Vì số tiền bác Thời phải trả sau hai năm là 2 420 000 nên ta có phương trình:

2 000 000.(1 + x)² = 2 420 000.

$\iff {\left(1+x\right)}^2=$2 420 000 : 2 000 000

⇔ (1 + x)² = 1,21

⇔ 1 + x = 1,1 (Vì 1 + x > 0)

⇔ x = 0,1 = 10%.

Vậy lãi suất ngân hàng là 10%  trên năm.

Bài 3: Một xuồng du lịch đi từ thành phố Cà Mau đến Đất Mũi theo một đường sông dài 120km. Trên đường đi, xuồng có nghỉ lại 1 giờ ở thị trấn Năm Căn. Khi về, xuồng đi theo đường khác dài hơn đường lúc đi 5km và với vận tốc nhỏ hơn vận tốc lúc đi là 5km/h. Tính vận tốc của xuồng lúc đi, biết rằng thời gian về bằng thời gian đi.

Lời giải

Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5). Vì lúc về xuồng đi với vận tốc nhỏ hơn vận tốc lúc đi 5km/h ⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).

Vì xuồng có nghỉ lại ở thị trấn Năm Căn 1h nên thời gian xuồng đi từ thành phố Cà Mau đến Đất Mũi là: $\frac{120}{x}$ + 1 (h)

Do lúc về xuống đi đường khác với quãng đường dài hơn quãng đường ban đầu 5km nên quãng đường về là: 120 + 5 = 125 km

Thời gian xuông đi từ Đất Mũi về thành phố Cà Mau là: $\frac{125}{x-5}$(h).

Vì thời gian về bằng thời gian đi nên ta có phương trình:

$\frac{120}{x}+1=\frac{125}{x-5}$

$\iff \frac{120+x}{x}=\frac{125}{x-5}$

$\iff \left(120+x\right)\left(x-5\right)=125x$

$\iff 120x+x^2-5x-600-125x=0$

$\iff x^2-10x-600=0$

Ta có: a = 1; b = -10; c = -600

$\Delta$ = $b^2-4ac={\left(-10\right)}^2-\mathrm{4.1.}\left(-600\right)=2500$

$\Rightarrow \sqrt{\Delta }=\sqrt{2500}=50$

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{10+50}{2}=30$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{10-50}{2}=-20$

Vì x > 5 nên chỉ có x = 30 thỏa mãn điều kiện.

Vậy vận tốc xuồng lúc đi là 30km/h.

Bài 4: Đố em tìm được một số mà một nửa của nó trừ đi một nửa đơn vị rồi nhân một nửa của nó bằng một nửa đơn vị.

Lời giải

Gọi số cần tìm là x $\Rightarrow$ Một nửa số đó là $\frac{x}{2}$.

+ Một nửa của x trừ đi một nửa đơn vị rồi nhân với một nửa của x là:

$\left(\frac{x}{2}-\frac{1}{2}\right).\frac{x}{2}$

Vì một nửa của x trừ đi một nửa đơn vị rồi nhân một nửa của x bằng một nửa đơn vị nên ta có phương trình:

$\left(\frac{x}{2}-\frac{1}{2}\right).\frac{x}{2}$ = $\frac{1}{2}$

$\iff \frac{\left(x-1\right)}{2}.\frac{x}{2}=\frac{1}{2}$

$\iff \frac{x\left(x-1\right)}{4}=\frac{1}{2}$

$\iff x^2-x=4.\frac{1}{2}$

$\iff x^2-x=2$

$\iff x^2-x-2=0$

Ta có: a = 1; b = -1; c = -2.

$\Delta =1^2-\mathrm{4.1.}\left(-2\right)=1+8$ = 9.

$\Rightarrow \sqrt{\Delta }=3$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{1+3}{2}=2$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{1-3}{2}=-1$

Vậy số cần tìm là 2 hoặc -1.

Bài 5: Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm hai số đó.

Lời giải

Gọi hai số tự nhiên liên tiếp cần tìm là x và x + 1 (x ∈ N).

Tích của hai số là: x(x + 1) = x² + x.

Tổng hai số là : x + x + 1 = 2x + 1.

Theo bài ra ta có phương trình : x² + x = 2x + 1 + 109

⇔ x² – x – 110 = 0

Có a = 1; b = -1; c = -110 ⇒ Δ = (-1)² – 4.1.(-110) = 441.

⇒ Phương trình có hai nghiệm:

Trong hai nghiệm chỉ có nghiệm x = 11 thỏa mãn điều kiện.

Vậy hai số tự nhiên cần tìm là 11 và 12.

Bài 6: Một mảnh đất hình chữ nhật có diện tích 240 m². Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì diện tích mảnh đất không đổi. Tính kích thước của mảnh đất.

Lời giải

Gọi chiều rộng của mảnh đất là x (m, x > 0).

Diện tích bằng 240 m² ⇒ Chiều dài mảnh đất là: 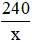 (m).

Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:

Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:

Có a = 1; b = 3; c = -180 ⇒ Δ = 3² – 4.1.(-180) = 729

Phương trình có hai nghiệm:

Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.

Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Bài 7: Bác Hiệp và cô Liên đi xe đạp từ làng lên tỉnh trên quãng đường dài 30km, khởi hành cùng một lúc. Vận tốc xe của bác Hiệp lớn hơn vận tốc xe của cô Liên là 3km/h nên bác Hiệp đã đến tỉnh trước cô Liên nửa giờ. Tính vận tốc xe của mỗi người.

Lời giải

Gọi vận tốc xe của cô Liên là x (km/h, x > 0).Vì vận tốc xe của bác Hiệp lớn hơn vận tốc xe của cô Liên 3km/h ⇒ Vận tốc xe của bác Hiệp là: x + 3 (km/h).

Thời gian cô Liên đi từ làng lên tỉnh là $\frac{30}{x}$(h)

Thời gian bác Hiệp đi từ làng lên tỉnh là $\frac{30}{x+3}$(h)

Vì thời gian đi của bác Hiệp ít hơn thời gian đi của cô Liên là nửa giờ nên ta có phương trình:

$\frac{30}{x}-\frac{30}{x+3}=0,5$

$\iff \frac{30.\left(x+3\right)}{x.\left(x+3\right)}-\frac{30.x}{x.\left(x+3\right)}=0,5$

$\iff \frac{30x+90}{x\left(x+3\right)}-\frac{30x}{x\left(x+3\right)}=0,5$

$\iff \frac{30x+90-30x}{x\left(x+3\right)}=0,5$

$\iff \frac{90}{x\left(x+3\right)}=0,5$

$\iff 90=0,5.x.\left(x+3\right)$

$\iff 90=0,5x^2+1,5x$

$\iff 0,5x^2+1,5x-90=0$ (*)

Giải (*)

Ta có: a = 0,5; b = 1,5; c = -90

$\Delta ={\left(1,5\right)}^2-4.0,5.\left(-90\right)=182,25$ > 0

$\Rightarrow \sqrt{\Delta }=13,5$

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-1,5+13,5}{2.0,5}=12$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-1,5-13,5}{2.0,5}=-15$

Kết hợp với điều kiện đề bài ta nhận thấy chỉ có x = 12km/h thỏa mãn.

Vậy vận tốc của cô Liên là 12km/h

Vận tốc của bác Hiệp là 15km/h.

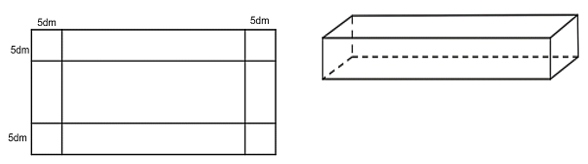
Bài 8: Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 5dm để làm thành một cái thùng hình hộp chữ nhật không nắp có dung tích 1500dm³ (h.15). Hãy tính kích thước của miếng tôn lúc đầu, biết rằng chiều dài của nó gấp đôi chiều rộng.

Hình 15

Lời giải

Gọi chiều rộng của miếng tôn là x(dm), (x > 10)

Vì chiều dài gấp 2 lần chiều rộng nên chiều dài miếng tôn là 2x (dm)

Khi làm thành một cái thùng không đáy với việc cắt bỏ như hình vẽ thì chiều dài của cái thùng đó là 2x – 10 (dm), chiều rộng của cái thùng đó là x – 10 (dm) và chiều cao của cái thùng đó là 5dm.

Vì dung tích của thùng là 1500$d{m}^3$ nên ta có phương trình:

$\left(2x-10\right).\left(x-10\right).5=1500$

$\iff \left(2x^2-20x-10x+100\right).5=1500$

$\iff 2x^2-20x-10x+100=1500:5$

$\iff 2x^2-30x+100=300$

$\iff 2x^2-30x+100-300=0$

$\iff 2x^2-30x-200=0$

$\iff x^2-15x-100=0$

Ta có: a = 1; b = -15; c = -100

$\Delta ={\left(-15\right)}^2-\mathrm{4.1.}\left(-100\right)=625>0$

$\Rightarrow \sqrt{\Delta }=25$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{15+25}{2.1}=20$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{15-25}{2.1}=-5$

Kết hợp với điều kiện ta thấy chỉ có x = 20 thỏa mãn điều kiện.

Vậy chiều rộng của miếng tôn lúc đầu là 20 dm

Chiều dài miếng tôn lúc đầu là 40 dm

Xem thêm các dạng bài tập toán hay khác:

50 Bài tập Giải bài toán bằng cách lập phương trình (có đáp án năm 2023)

50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)

50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)

50 Bài tập Giải bài toán bằng cách lập hệ phương trình (có đáp án năm 2023)

50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)