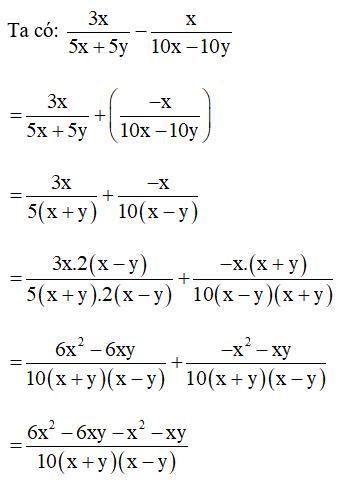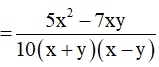Phân thức đại số
Kiến thức cần nhớ
1. Định nghĩa phân thức đại số
trong đó A, B là những đa thức và B khác đa thức 0.
Trong đó:
+ A được gọi là tử thức (hay gọi là tử).
+ B được gọi là mẫu thức (hay gọi là mẫu).
Chú ý:
+ Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
+ Số 0, số 1 cũng là một phân thức đại số.
Ví dụ. Ta có các phân thức đại số
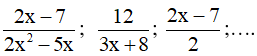
2. Hai phân thức bằng nhau
Hai phân thức và gọi là bằng nhau nếu A . D = B . C. Ta viết:
nếu A . D = B . C.
Ví dụ.
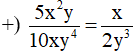 vì 5x2y . 2y3 = 10xy4 . x (do cùng bằng 10 x2y4).
vì 5x2y . 2y3 = 10xy4 . x (do cùng bằng 10 x2y4).
![]() vì x . (2x + 4) = 2 . (x2 + 2x) (do cùng bằng 2x2 + 4x).
vì x . (2x + 4) = 2 . (x2 + 2x) (do cùng bằng 2x2 + 4x).
3. Tính chất cơ bản của phân thức
- Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân thức bằng phân thức đã cho:
(M là một đa thức khác đa thức 0).
- Nếu chia cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân thức bằng phân thức đã cho:
(N là một đa thức khác đa thức 0).
Ví dụ. Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết:
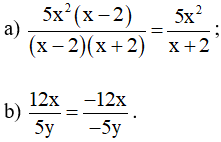
Hướng dẫn giải:
a) Ta chia cả tử và mẫu của phân thức cho đa thức x – 2, ta có:
Vậy .
b) Nhân cả tử và mẫu của phân thức với (– 1) ta được:
Vậy .
4. Quy tắc đổi dấu
Nếu đổi dấu cả tử và mẫu của một phân thức thì nhận được phân thức mới bằng phân thức đã cho:
Ví dụ. Dùng quy tắc đổi dấu điền đa thức thích hợp vào chỗ chấm trong mỗi đẳng thức sau:
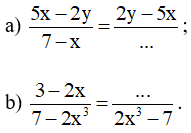
Hướng dẫn giải:
a) Áp dụng quy tắc đổi dấu ta có:
Vậy đa thức cần điền vào chỗ chấm là x – 7.
b) Áp dụng quy tắc đổi dấu ta có:
.
Vậy đa thức cần điền vào chỗ chấm là 2x – 3.
5. Cách rút gọn phân thức
Muốn rút gọn một phân thức đại số ta có thể:
+ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung.
Chú ý: Có khi cần đổi dấu tử hoặc mẫu thức để nhận ra nhân tử chung của tử và mẫu (cần lưu ý tới tính chất A = – (– A)).
Ví dụ . Rút gọn phân thức .
Hướng dẫn giải:
Ta có:
Ví dụ . Rút gọn phân thức .
Hướng dẫn giải:
Ta có:
6. Quy đồng mẫu thức nhiều phân thức
6.1. Khái niệm
Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.
Ta thường kí hiệu “mẫu thức chung” bởi MTC.
6.2. Tìm mẫu thức chung
Khi quy đồng mẫu thức nhiều phân thức, muốn tìm mẫu thức chung ta có thể làm như sau:
• Phân tích mẫu thức của các phân thức đã cho thành nhân tử;
• Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau:
+ Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số ở các mẫu thức của các phân thức đã cho. (Nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử bằng số của mẫu thức chung là BCNN của chúng).
+ Với mỗi luỹ thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn luỹ thừa với số mũ cao nhất.
Ví dụ . Tìm mẫu thức chung của hai phân thức và .
Hướng dẫn giải:
+ Phân tích các mẫu thức thành nhân tử:
3x2 – 6x + 3 = 3(x2 – 2x + 1) = 3(x – 1)2
7x2 – 7x = 7x(x – 1)
+ Chọn mẫu thức chung:
Mẫu thức chung của số nguyên là BCNN(3, 7) = 21.
Mẫu thức chung của lũy thừa x là x.
Mẫu thức chung của lũy thừa (x – 1) là (x – 1)2.
Do đó: MTC = 21x(x – 1)2.
Vậy mẫu thức chung của hai phân thức đã cho là 21x(x – 1)2.
6.3. Quy đồng mẫu thức
Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
- Tìm nhân tử phụ của mỗi mẫu thức;
- Nhân tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Ví dụ . Quy đồng mẫu thức hai phân thức: và .
Hướng dẫn giải:
Ở ví dụ trên ta đã tìm được mẫu thức chung của hai phân thức và là 21x(x – 1)2.
+ Vì 21x(x – 1)2 = 7x . 3(x2 – 2x + 1) = 7x . (3x2 – 6x + 3) nên nhân tử phụ của mẫu thức thứ nhất là 7x, ta nhân cả tử và mẫu của phân thức thứ nhất với nhân tử phụ 7x, ta được:
+ Vì 21x(x – 1)2 = 3. 7x.(x – 1) . (x – 1) = 3(x – 1) . (7x2 – 7x) nên nhân tử phụ của mẫu thức thứ hai là 3(x – 1), ta nhân cả tử và mẫu của phân thức thứ hai với nhân tử phụ 3(x – 1), ta được:
7. Phép cộng phân thức
7.1. Cộng hai phân thức cùng mẫu thức
Quy tắc: Muốn cộng hai phân thức cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức.
Ta có thể viết: (A, B, C là các đa thức, đa thức C khác đa thức 0).
Ví dụ. Thực hiện phép cộng: .
Hướng dẫn giải:
Ta có:
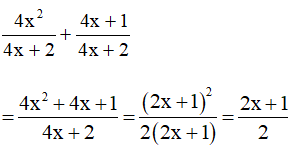
7.2. Cộng hai phân thức có mẫu thức khác nhau
Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
Ta có thể viết: (với A, B, C, D là các đa thức và B, D là đa thức khác đa thức 0).
Kết quả của phép cộng hai phân thức được gọi là tổng của hai phân thức ấy. Ta thường viết tổng này dưới dạng rút gọn.
Ví dụ . Thực hiện phép cộng: .
Hướng dẫn giải:
Ta có: x2 + 5x = x(x + 5)
2x + 10 = 2(x + 5)
Suy ra mẫu thức chung là: 2x(x + 5).
Khi đó ta có:
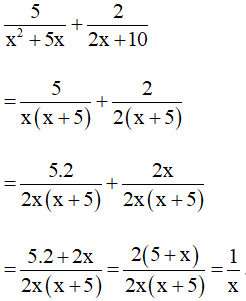
Chú ý: Phép cộng các phân thức cũng có các tính chất sau:
• Giao hoán: ;
• Kết hợp: .
Ví dụ .
Thực hiện phép tính sau:
Hướng dẫn giải:
Ta có:
(sử dụng tính chất giao hoán và kết hợp)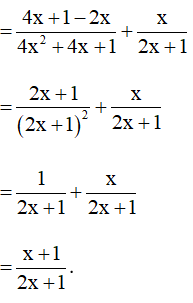
8. Phân thức đối
Hai phân thức được gọi là đối nhau nếu tổng của chúng bằng 0.
Tổng quát: Với phân thức ta có . Do đó:

Kí hiệu: Phân thức đối của phân thức được kí hiệu bởi .
Khi đó: và .
Ví dụ.
+ Phân thức đối của phân thức là .
+ Phân thức đối của phân thức là .
9. Phép trừ phân thức
10. Phép nhân phân thức
10.1. Quy tắc nhân hai phân thức
Muốn nhân hai phân thức với nhau, ta nhân các tử thức với nhau, các mẫu thức với nhau:
Ví dụ. Thực hiện phép nhân .
Hướng dẫn giải:
Ta có:
Phép nhân các phân thức có các tính chất:
+ Giao hoán: ;
+ Kết hợp: ;
+ Phân phối đối với phép cộng: .
Ví dụ. Thực hiện phép tính: .
Hướng dẫn giải:
Ta có:
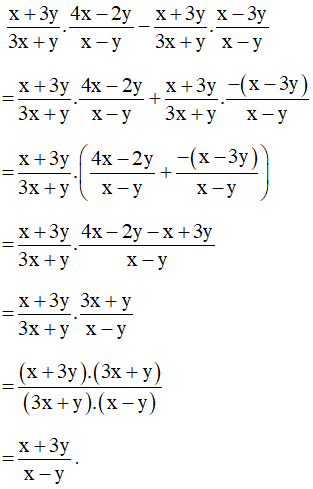
11. Phân thức nghịch đảo
Hai phân thức được gọi là nghịch đảo của nhau nếu tích của chúng bằng 1.
Tổng quát, nếu là một phân thức khác 0 thì , do đó:
+) là phân thức nghịch đảo của phân thức ;
+) là phân thức nghịch đảo của phân thức .
Ví dụ.
- Phân thức nghịch đảo của phân thức là phân thức .
- Phân thức nghịch đảo của phân thức là phân thức .
Quy tắc: Muốn chia phân thức cho phân thức khác 0, ta nhân phân thức với phân thức nghịch đảo của :
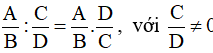
Ví dụ. Thực hiện phép chia: .
Hướng dẫn giải:
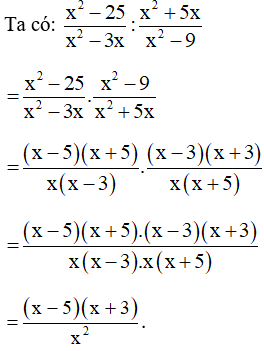
13. Biểu thức hữu tỉ
Mỗi biểu thức là một phân thức hoặc biểu thị một dãy phép toán cộng, trừ, nhân, chia trên những phân thức gọi là biểu thức hữu tỉ.
Ví dụ. Ta có các biểu thức hữu tỉ như: ; …
14. Biến đổi một biểu thức hữu tỉ thành một phân thức
Nhờ các quy tắc của các phép toán cộng, trừ, nhân, chia các phân thức, ta có thể biến đổi các biểu thức hữu tỉ thành một phân thức.
Ví dụ. Biến đổi biểu thức thành một phân thức.
Hướng dẫn giải:
Ta có:
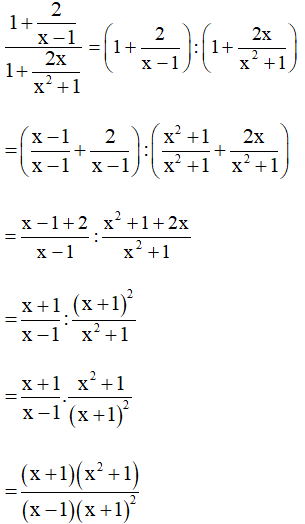
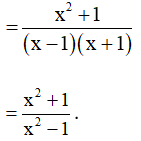
15. Giá trị của phân thức
Khi thực hiện các bài toán liên quan đến giá trị của phân thức:
+ Trước hết, phải tìm điều kiện của biến để giá trị tương ứng của mẫu thức khác 0: Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 là điều kiện để giá trị của phân thức được xác định.
+ Nếu tại giá trị của biến mà giá trị của phân thức được xác định thì phân thức ấy và phân thức được rút gọn có cùng một giá trị.
Để tính giá trị của phân thức, ta chỉ cần thay giá trị của biến vào phân thức đã được rút gọn rồi thực hiện tính như tính giá trị của biểu thức số.
Ví dụ. Cho phân thức .
a) Tìm điều kiện của x để giá trị của phân thức được xác định.
b) Tính giá trị của phân thức tại x = 2020.
Hướng dẫn giải:
a) Giá trị của phân thức được xác định với điều kiện x(x – 2) ≠ 0.
Mà một tích (của nhiều số) khác 0 khi mọi thừa số đều khác 0, do đó x ≠ 0 và x – 2 ≠ 0 hay chính là x ≠ 0 và x ≠ 2.
Vậy điều kiện để giá trị của phân thức được xác định là: x ≠ 0 và x ≠ 2.
b) Ta có: và x = 2020 thỏa mãn các điều kiện của biến nên có thể tính giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn .
Vậy giá trị của phân thức đã cho tại x = 2020 bằng .
Bài tập (có đáp án)
Bài tập vận dụng
Bài 1. Dùng định nghĩa hai phân thức bằng nhau, chứng tỏ rằng:
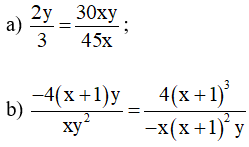
Hướng dẫn giải:
a) Ta có: 2y . 45x = 90xy
3 . 30xy = 90xy
Do đó: 2y . 45x = 3 . 30 xy
Vậy .
b) Ta có:
– 4(x + 1)y . [–x(x + 1)2y] = 4x . [(x + 1). (x + 1)2] . [y . y] = 4x(x + 1)3 . y2
xy2. 4(x + 1)3 = 4x(x + 1)3 . y2
Do đó: – 4(x + 1)y . [–x(x + 1)2y] = xy2 . 4(x + 1)3.
Vậy
Bài 2. Tìm điều kiện xác định của các phân thức sau:
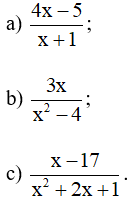
Hướng dẫn giải:
a) Phân thức có nghĩa khi x + 1 ≠ 0 hay x ≠ – 1.
Vậy điều kiện xác định của phân thức là x ≠ – 1.
b) Phân thức có nghĩa khi x2 – 4 ≠ 0 hay (x – 2)(x + 2) ≠ 0
Suy ra x ≠ 2 và x ≠ – 2.
Vậy điều kiện xác định của phân thức là x ≠ 2 và x ≠ – 2.
c) Phân thức có nghĩa khi x2 + 2x + 1 ≠ 0
hay (x + 1)2 ≠ 0
Suy ra x ≠ – 1 (do (x + 1)2 ≥ 0 với mọi x)
Vậy điều kiện xác định của phân thức là x ≠ – 1.
Bài 3. Chứng minh các đẳng thức sau:
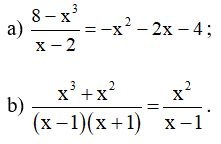
Hướng dẫn giải:
a) Ta có:
Vậy .
b) Ta có:
Vậy .
Bài 4. Hai phân thức sau có bằng nhau không?
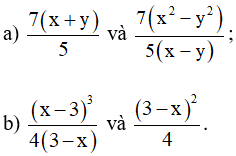
Hướng dẫn giải:
a) Ta có: x2 – y2 = (x – y).(x + y)
Do đó:
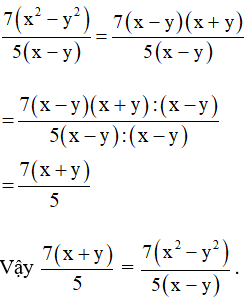
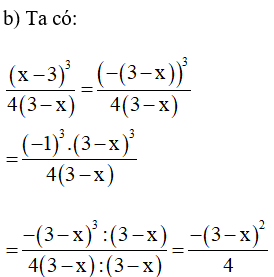
Vậy hai phân thức và không bằng nhau.
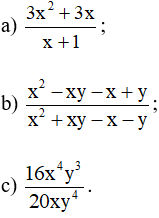
Hướng dẫn giải:
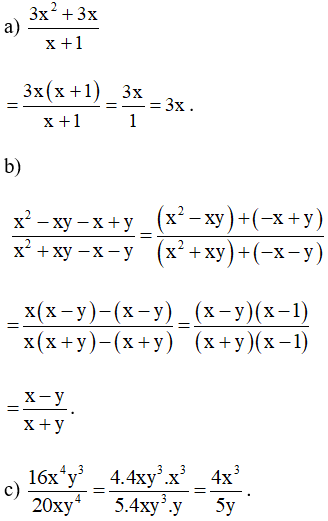
Bài 6. Rút gọn các phân thức sau:
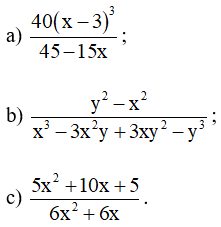
Hướng dẫn giải:
a)
b)
c)
Bài 7. Quy đồng mẫu thức các phân thức sau:
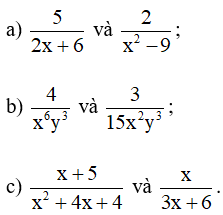
Hướng dẫn giải:
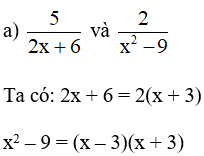
Do đó mẫu thức chung là 2(x + 3)(x – 3) = 2(x2 – 9).
Khi đó ta có:
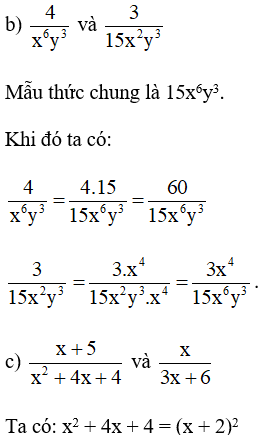
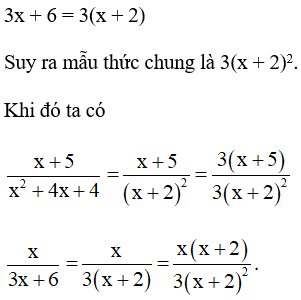
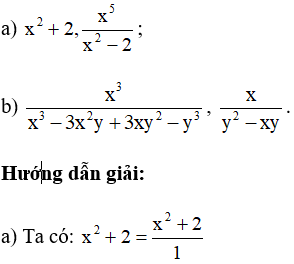
Mẫu thức chung là x2 – 2. Khi đó ta có:
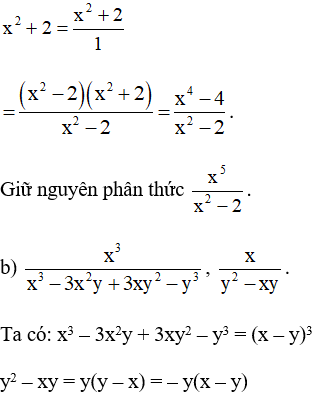
Suy ra mẫu thức chung là: – y(x – y)3.
Khi đó ta có:
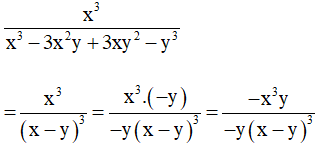
Bài 9. Làm tính cộng các phân thức sau:
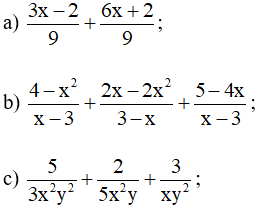
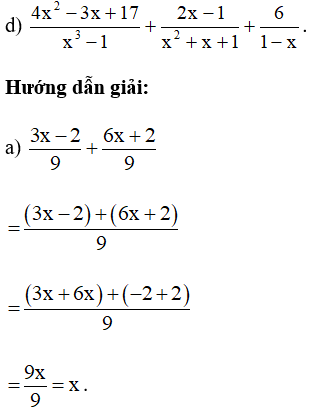
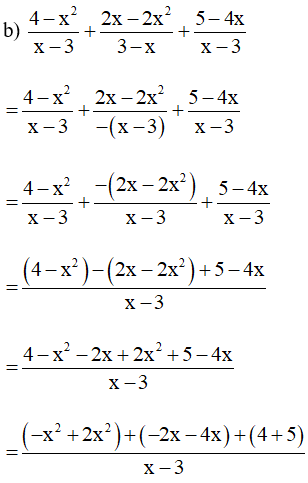
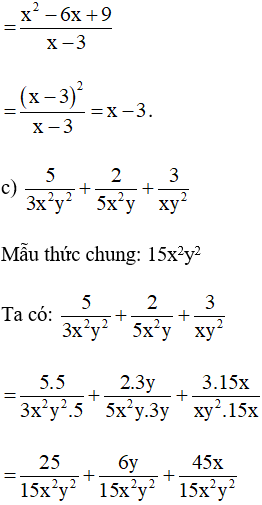
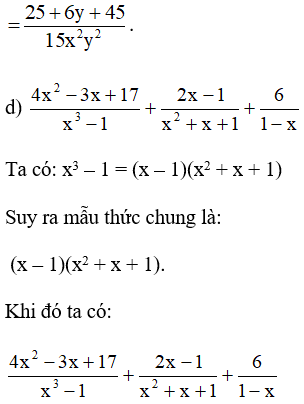
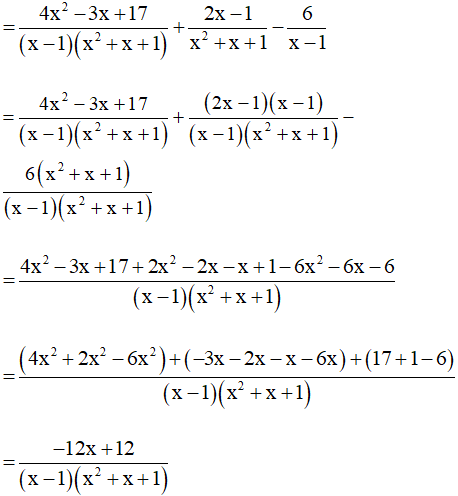
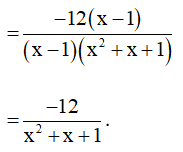
Bài 10. Rút gọn rồi tính giá trị của biểu thức
tại x = – 5.
Hướng dẫn giải:
Ta có: 6x + 36 = 6(x + 6)
Suy ra mẫu thức chung là: 6x(x + 6).
Khi đó ta có:
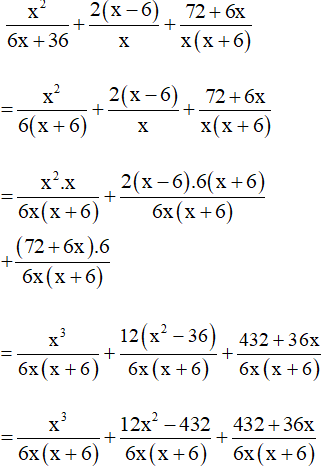
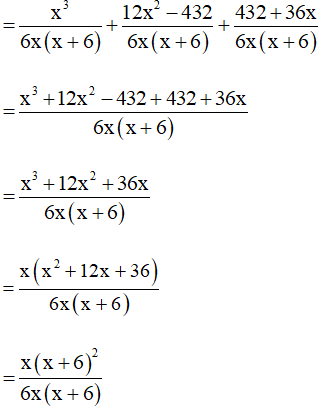

Bài 11. Thực hiện các phép tính sau:
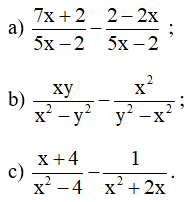
Hướng dẫn giải:
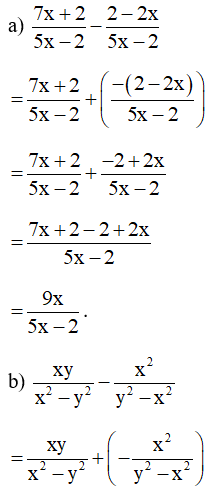
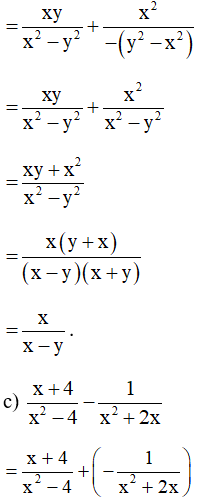
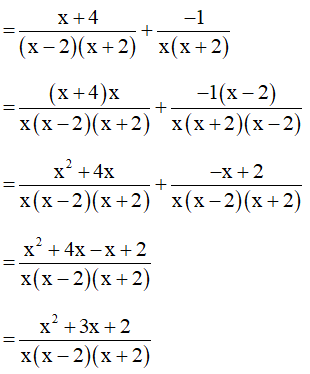
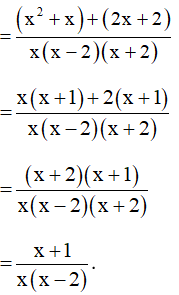
Bài 12. Tính .
Hướng dẫn giải:
Ta có: x3 + 1 = (x + 1)(x2 – x + 1)
Mẫu thức chung là (x + 1)(x2 – x + 1).
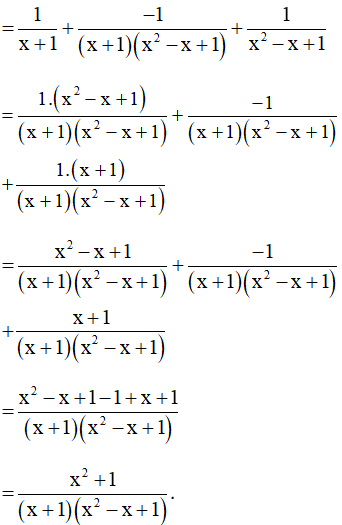
Bài 13. Chứng minh giá trị của biểu thức sau không phụ thuộc vào x.
.
Hướng dẫn giải:
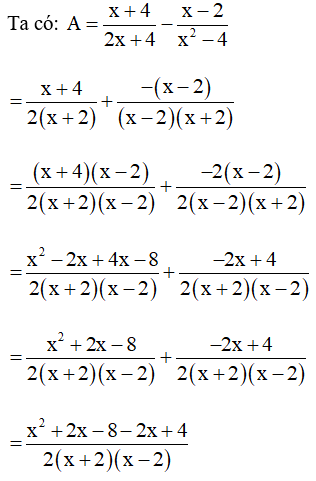
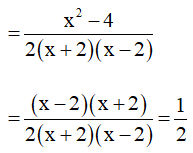
Vậy giá trị của biểu thức A không phụ thuộc vào biến x.
Bài 14. Tính:
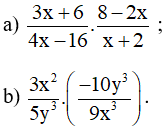
Hướng dẫn giải:
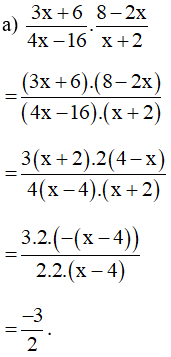
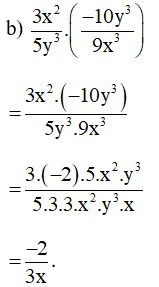
Bài 14. Thực hiện các phép tính sau:
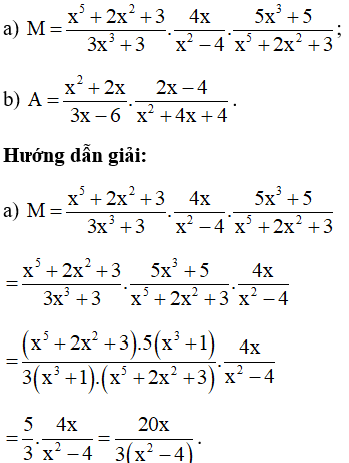
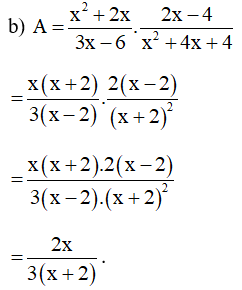
Bài 15. Rút gọn rồi tính giá trị của biểu thức
với x = 99.
Hướng dẫn giải:
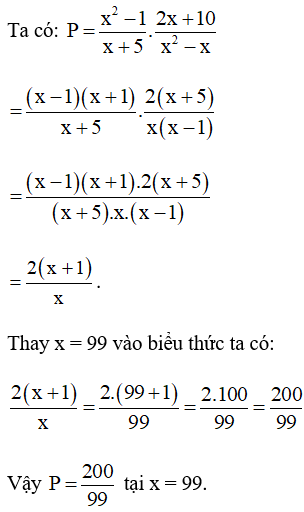
Bài 16. Thực hiện phép chia

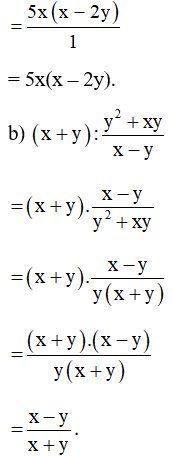
Bài 17. Thực hiện phép chia
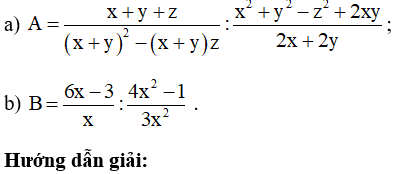
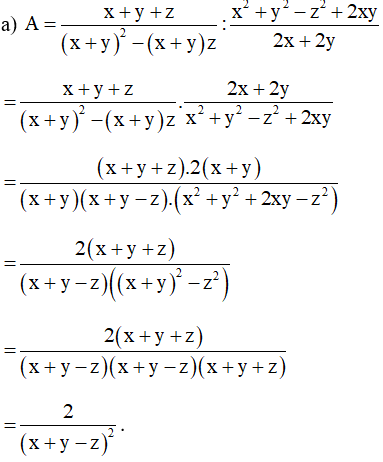
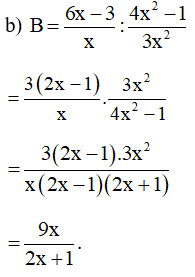
Bài 18. Tìm x biết:
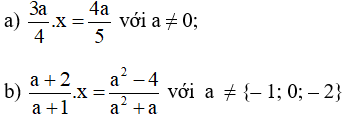
Hướng dẫn giải:
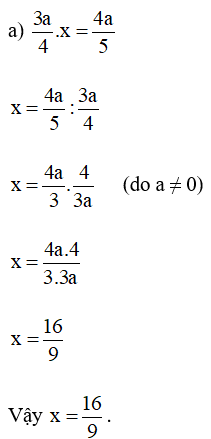
b) Vì a ≠ {– 1; 0; – 2} nên a + 1 ≠ 0; a + 2 ≠ 0 và a ≠ 0.
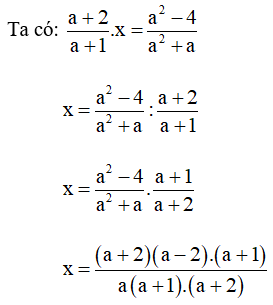
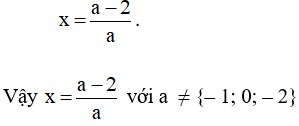
Bài 19. Giá trị của phân thức được xác định khi nào?
Hướng dẫn giải:
Ta có: phân thức xác định khi x2 – 4 ≠ 0.
Mà x2 – 4 = (x – 2)(x + 2)
Nên (x – 2)(x + 2) ≠ 0
Mà một tích khác 0 khi mọi thừa số đều khác 0.
Do đó: x – 2 ≠ 0 và x + 2 ≠ 0
Hay x ≠ 2 và x ≠ – 2.
Vậy giá trị của phân thức được xác định khi x ≠ 2 và x ≠ – 2.
Bài 20. Tìm giá trị của x để giá trị phân thức bằng 0.
Hướng dẫn giải:
Điều kiện xác định của phân thức là x3 – 4x ≠ 0.
Mà x3 – 4x = x(x2 – 4) = x. (x – 2).(x + 2)
Nên x.(x – 2) . (x + 2) ≠ 0
Suy ra x ≠ 0, x – 2 ≠ 0 và x + 2 ≠ 0.
Hay x ≠ 0, x ≠ 2 và x ≠ – 2.
Ta có:
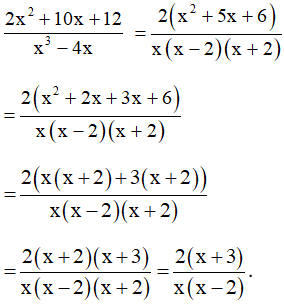
Ta có phân thức bằng 0 khi .
Suy ra 2(x + 3) = 0 ⇒ x = – 3 (thỏa mãn điều kiện).
Vậy x = – 3 thì giá trị phân thức bằng 0.
Bài 21. Biến đổi biểu thức thành phân thức đại số.
Hướng dẫn giải:
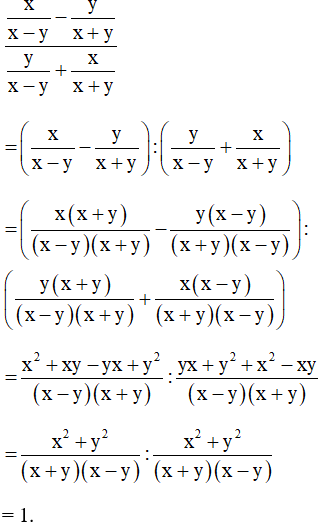
Bài 22. Cho .
a) Rút gọn N;
b) Tính giá trị của N tại x = 15.
Hướng dẫn giải:
a) Ta có: x2 – 7x + 10 = x2 – 2x – 5x + 10 = x(x – 2) – 5(x – 2) = (x – 2)(x – 5)
x2 – 4 = (x + 2)(x – 2)
Do đó điều kiện xác định của biểu thức N là
Hay x – 2 ≠ 0, x + 2 ≠ 0, x – 5 ≠ 0.
Suy ra x ≠ 2, x≠ – 2 và x ≠ 5.
Ta có
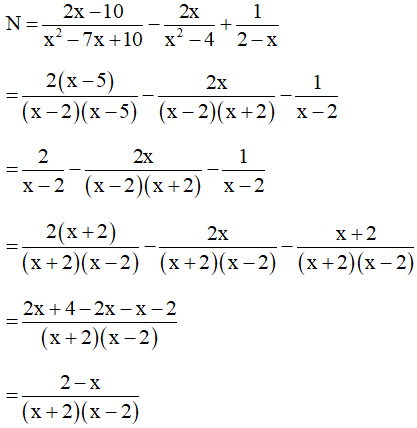
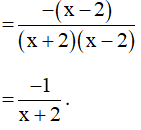
Vậy với x ≠ 2, x≠ – 2 và x ≠ 5.
b) Có x = 15 thỏa mãn các điều kiện của biến x.
Khi đó thay x = 15 vào N ta được:
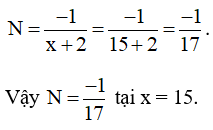
Bài tập tự luyện
Xem thêm các dạng Toán hay, chọn lọc khác :
60 Bài tập về Tính chất cơ bản của phân thức (có đáp án năm 2023)
60 Bài tập về Rút gọn phân thức (có đáp án năm 2023)
60 Bài tập về Quy đồng mẫu thức nhiều phân thức (có đáp án năm 2023)
60 Bài tập phép cộng các phân thức đại số (có đáp án năm 2023)
60 Bài tập về phép trừ các phân thức đại số (có đáp án năm 2023)