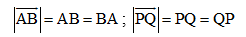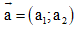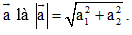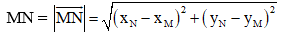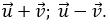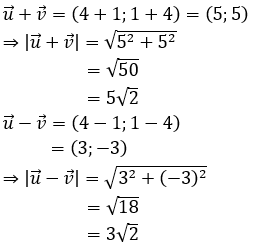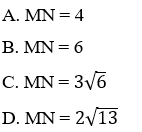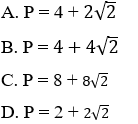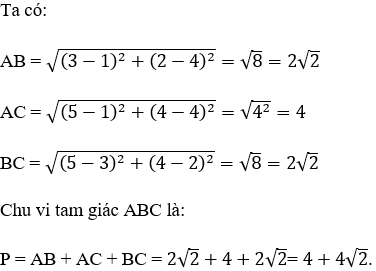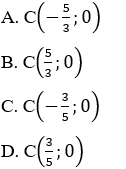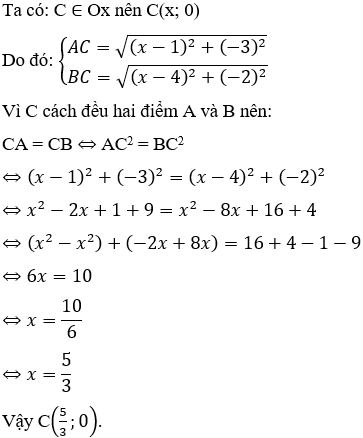20 bài tập tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ (2024) cực hay, chi tiết

Cách tính độ dài vectơ, khoảng cách giữa hai điểm trong hệ tọa độ

1. Phương pháp giải

1.1. Độ dài vectơ

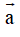
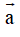
- Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vecto  được ký hiệu là ||.

Do đó đối với các vectơ 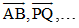 ta có:

- Phương pháp: muốn tính độ dài vectơ, ta tính độ dài cách giữa điểm đầu và điểm cuối của vectơ.

- Trong hệ tọa độ: Cho 

Độ dài vectơ 

1.2. Khoảng cách giữa hai điểm trong hệ tọa độ

Áp dụng công thức sau

Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm M(x_M;y_M) và N(x_N;y_N) là

2. Ví dụ minh họa

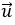
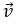
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ =(4;1) và =(1;4). Tính độ dài vectơ 

Hướng dẫn giải:

Ta có:

Ví dụ 2: Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1; -2) và N (-3; 4).

Hướng dẫn giải:

Đáp án D

3. Bài tập vận dụng (có đáp án)

Bài 1: Cho hình chữ nhật ABCD tâm O. Biết AB = 2a và AD = a. Tính độ dài  $\left|\overrightarrow{AB}+\overrightarrow{BC}\right|$.

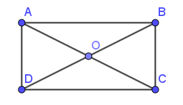
Lời giải:

Do ABCD là hình chữ nhật nên ta có: BC = AD = a

Xét tam giác ABC vuông tại B (do ABCD là hình chữ nhật)

Áp dụng định lí Py-ta-go ta có:

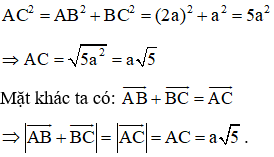
Bài 2: Cho hình vuông ABCD cạnh a, tâm O. Tính độ dài $\left|\frac{1}{2}\overrightarrow{AC}\right|$.

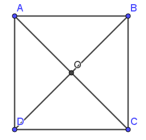
Lời giải:

Xét tam giác ABC vuông cân tại B (do ABCD là hình vuông) :

Áp dụng định lí Py-ta-go ta có:

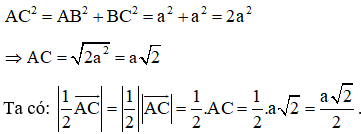
Bài 3: Cho vectơ $\overrightarrow{a}=(1;6m)$. Tìm m để độ dài $\left|\overrightarrow{a}\right|=5$.

Lời giải:

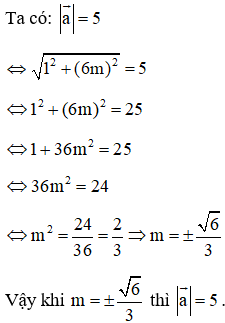
Bài 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4), B(3; 2), C(5; 4). Chu vi P của tam giác đã cho.

Hướng dẫn giải:

Đáp án B

Bài 5: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Khẳng định nào sau đây là đúng?

A. Tứ giác ABCD là hình bình hành

B. Tứ giác ABCD là hình thoi

C. Tứ giác ABCD là hình thang cân

D. Tứ giác ABCD không nội tiếp được đường tròn

Hướng dẫn giải:

Từ (1) và (2) suy ra ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân).

Đáp án C

Bài 6: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;3) và B(4;2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B.

Hướng dẫn giải:

Đáp án B

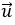
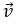
Bài 7: Trong mặt phẳng tọa độ Oxy, cho hai vectơ =(4;1) và =(1;4). Tính độ dài vectơ 

Hướng dẫn giải:

Ta có:

Bài 8: Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1; -2) và N (-3; 4).

Hướng dẫn giải:

Đáp án D

Bài 9: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4), B(3; 2), C(5; 4). Chu vi P của tam giác đã cho.

Hướng dẫn giải:

Đáp án B

Bài 10: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Khẳng định nào sau đây là đúng?

A. Tứ giác ABCD là hình bình hành

B. Tứ giác ABCD là hình thoi

C. Tứ giác ABCD là hình thang cân

D. Tứ giác ABCD không nội tiếp được đường tròn

Hướng dẫn giải:

Đáp án C

Từ (1) và (2) suy ra ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân).

Bài 12: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;3) và B(4;2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B.

Hướng dẫn giải:

Đáp án B

Đáp án B

Bài 13: Cho tam giác $ABC$ đều cạnh a. Khi đó $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|$ bằng:

     A. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}.$                       B. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\frac{a\sqrt{3}}{2}.$

     C. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2a.$                         D. Một đáp án khác.

Hướng dẫn giải:

Chọn A

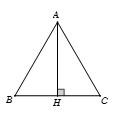
Gọi  H là trung điểm của  $BC\Rightarrow AH\perp BC.$

Suy ra $AH=\frac{BC\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}.$

Ta lại có $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|2\overrightarrow{AH}\right|=2.\frac{a\sqrt{3}}{2}=a\sqrt{3}$.

Bài 14: Cho tam giác vuông cân $ABC$ tại A có $AB=a$. Tính   $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|.$

     A. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{2}.$                        B.   $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\frac{a\sqrt{2}}{2}.$     

     C. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2a.$                           D.  $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a.$

Hướng dẫn giải:

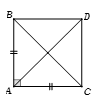
Chọn A. 

Gọi D là điểm thỏa mãn tứ giác $ABDC$ là hình vuông.

$\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|=AD=a\sqrt{2}.$

Bài 15: Cho tam giác ABC vuông cân đỉnh C, $AB=\sqrt{2}$. Tính độ dài của $\overrightarrow{AB}+\overrightarrow{AC}.$

     A. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\sqrt{5}.$                        B. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\sqrt{5}.$

     C.  $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\sqrt{3}.$                        D. $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\sqrt{3}.$

Hướng dẫn giải:

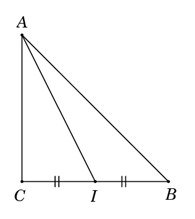
Chọn A.

Ta có  $AB=\sqrt{2}\stackrel{}{\to }AC=CB=1.$

Gọi I là trung điểm $BC\stackrel{}{\to }AI=\sqrt{A{C}^2+C{I}^2}=\frac{\sqrt{5}}{2}.$

Khi đó   $\overrightarrow{AC}+\overrightarrow{AB}=2\overrightarrow{AI}\stackrel{}{\to }\left|\overrightarrow{AC}+\overrightarrow{AB}\right|=2\left|\overrightarrow{AI}\right|=2.\frac{\sqrt{5}}{2}=\sqrt{5}.$

Xem thêm các dạng bài tập toán hay khác:

80 Bài tập Tổng và hiệu của hai vectơ (có đáp án năm 2023)

80 Bài tập về vectơ trong mặt phẳng tọa độ (có đáp án năm 2024)

90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2023)

30 bài tập về Khoảng cách giữa hai đường thẳng song song (2024) có đáp án

20 Bài tập về Góc giữa đường thẳng và mặt phẳng (2024) hay nhất