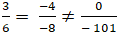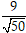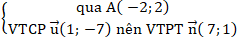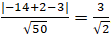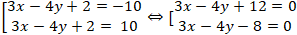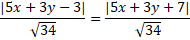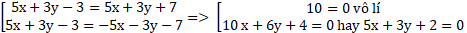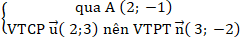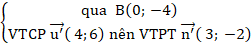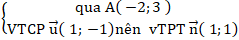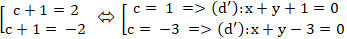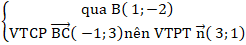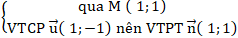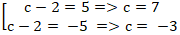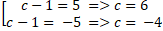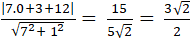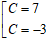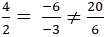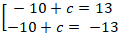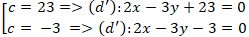30 bài tập về Khoảng cách giữa hai đường thẳng song song (2024) có đáp án

Tìm khoảng cách giữa hai đường thẳng song song

1. Lý thuyết tổng hợp

- Cho hai đường thẳng d và d’ song song với nhau. Khoảng cách hai đường thẳng này bằng khoảng cách từ một điểm bất kì của đường thẳng này đến đường thẳng kia.

- Để tính khoảng cách hai đường thẳng song song ta cần:

+ Đưa phương trình hai đường thẳng về dạng tổng quát.

+ Lấy một điểm A bất kì thuộc đường thẳng d.

+ Tính khoảng cách từ điểm A đến đường thẳng d’ .

+ Kết luận: d(d; d’) = d(A; d’) .

2. Các công thức

- Cho đường thẳng d: ax + by + c = 0 và d’: ax + by + c’  (d // d’).

+ Lấy điểm A(x’; y’) thuộc d

+ Tính khoảng cách từ A đến d’, có: $d(d;d\text{'})=d(A;d\text{'})=\frac{\left|ax\text{'}+by\text{'}+c\text{'}\right|}{\sqrt{a^2+b^2}}$

3. Ví dụ minh họa

Ví dụ minh họa 1:  Cho hai đường thẳng song song là d: 3x + 2y + 1 = 0 và d’: 3x + 2y - 1 = 0. Tìm khoảng cách giữa d và d’.

Lời giải:

Có điểm A(-1; 1) thuộc đường thẳng d: 3x + 2y + 1 = 0

Ta có:

$$\begin{gathered} d(d;d\text{'})=d(A;d\text{'}) \\ =\frac{\left|3.(-1)+2.1-1\right|}{\sqrt{3^2+2^2}}=\frac{2\sqrt{13}}{13} \end{gathered}$$

Ví dụ minh họa 2: Cho hai đường thẳng song song là d: x + 5y – 1 = 0 và d’: x + 5y + 4 = 0. Tìm khoảng cách giữa d và d’.

Lời giải:

Có điểm A(-4; 1) thuộc đường thẳng d: x + 5y – 1 = 0

Ta có: 

$$\begin{gathered} d(d;d\text{'})=d(A;d\text{'}) \\ =\frac{\left|-4+5.1+4\right|}{\sqrt{1^2+5^2}}=\frac{5\sqrt{26}}{26} \end{gathered}$$

4. Bài tập tự luyện (có đáp án)

Bài 1:  Cho hai đường thẳng song song là d: 3x + 4y + 2 = 0 và d’: 3x + 4y + 4 = 0. Tìm khoảng cách giữa d và d’.

Lời giải:

Có điểm A(2; -2) thuộc đường thẳng d: 3x + 4y + 2= 0

Ta có:

$$\begin{gathered} d(d;d\text{'})=d(A;d\text{'}) \\ =\frac{\left|3.2+4.(-2)+4\right|}{\sqrt{3^2+4^2}}=\frac{2}{5} \end{gathered}$$

Bài 2: Khoảng cách giữa hai đường thẳng ∆: 6x - 8y - 101 = 0 và d: 3x - 4y = 0 là:

A. 10, 1                B. 1,01                      C. 12                      D. √101 .

Lời giải:

+ Ta có: 

⇒ Hai đường thẳng đã cho song song với nhau: d // ∆.

+ Lấy điểm O( 0;0) thuộc đường thẳng d.

+ Do hai đường thẳng d và ∆ song song với nhau nên

d(∆; d) = d ( O; ∆) = 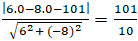 = 10,1

Chọn A.

Bài 3: Tính khoảng cách giữa hai đường thẳng d: 7x + y - 3 = 0 và ∆:  .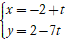

A. 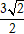                  B. 15                     C. 9                         D. 

Lời giải:

+ Ta đưa đường thẳng ∆ về dạng tổng quát:

∆: 

⇒ Phương trình ∆: 7( x + 2) + 1( y - 2) = 0 hay 7x + y + 12 = 0

Ta có: 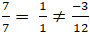 nên d // ∆

⇒ d(d;Δ) = d(A;d) = 

Chọn A.

Bài 4: Tập hợp các điểm cách đường thẳng ∆: 3x - 4y + 2 = 0 một khoảng bằng 2 là hai đường thẳng có phương trình nào sau đây?

A. 3x - 4y + 8 = 0 hoặc 3x - 4y + 12 = 0.    

B. 3x - 4y - 8 = 0 hoặc 3x - 4y + 12 = 0.

C. 3x - 4y - 8 = 0 hoặc 3x - 4y - 12 = 0.    

D. 3x - 4y + 8 = 0 hoặc 3x - 4y - 12 = 0.

Lời giải:

Gọi điểm M (x ; y) là điểm cách đường thẳng ∆ một khoảng bằng 2. Suy ra :

d(M(x; y); Δ) = 2 ⇔ 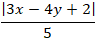 = 2

|3x - 4y + 2| = 10 ⇒ 

Vậy tập hợp các điểm cách ∆ một khoảng bằng 2 là hai đường thẳng :

3x - 4y + 12 = 0 và 3x - 4y - 8 = 0

Chọn B.

Bài 5: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d₁: 5x + 3y - 3 = 0 và d₂: 5x + 3y + 7 = 0 song song nhau. Đường thẳng d vừa song song và cách đều với d₁; d₂ là:

A. 5x + 3y - 2 = 0    

B. 5x + 3y + 4 = 0    

C. 5x + 3y + 2 = 0    

D. 5x + 3y - 4 = 0

Lời giải:

Lấy điểm M ( x; y) thuộc đường thẳng d. Suy ra:

d(M(x; y); d₁)=d(M(x; y); d₂) ⇔ 

⇔ 

Đường thẳng d: 5x + 3y + 2 song song với hai đường thẳng d₁ và d₂.

Vậy đường thẳng d thỏa mãn là: 5x + 3y + 2 = 0

Chọn C.

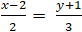
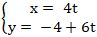
Bài 6: Cho đường thẳng d:  và đường thẳng ∆:  . Tính khoảng cách hai đường thẳng này.

A. 1                     B. 0.                       C. 2                                  D. 3

Lời giải:

+ Đường thẳng d: 

⇒ Phương trình d: 3(x - 2) – 2(y + 1) = 0 hay 3x - 2y - 8 = 0

+ Đường thẳng ∆: 

⇒ Phương trình ∆: 3(x - 0) – 2(y + 4) = 0 hay 3x - 2y - 8 = 0

⇒ hai đường thẳng này trùng nhau nên khoảng cách hai đường thẳng này là 0.

Chọn B.

Bài 7: Cho hai đường thẳng d: x + y - 2 = 0 và đường thẳng ∆: 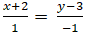 . Viết phương trình đường thẳng d’// d sao cho khoảng cách hai đường thẳng d’ và ∆ là √2.

A. x + y - 1 = 0    

B. x + y + 1= 0    

C. x + y - 3 = 0    

D. Cả B và C đúng.

Lời giải:

+ Do đường thẳng d’// d nên đường thẳng d có dạng (d’) : x + y + c = 0( c ≠ -2)

+ Đường thẳng ∆: 

⇒ Phương trình ∆: 1(x + 2) + 1(y - 3) = 0 hay x + y - 1 = 0.

+ Lấy điểm M ( 1; 0) thuộc ∆.

Để khoảng cách hai đường thẳng d’ và ∆ bằng 2 khi và chỉ khi:

d( d’; ∆) = d( M; d’) = 2

⇔  = √2 ⇔ |1 + c| = 2

⇔

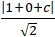
Vậy có hai đường thẳng thỏa mãn là : x + y + 1 = 0 và x + y - 3 = 0

Chọn D.

Bài 8: Cho tam giác ABC có B( 1; -2) và C( 0; 1). Điểm A thuộc đường thẳng
d: 3x+ y= 0 .Tính diện tích tam giác ABC.

A. 1                           B. 3                                C. 0,5                               D. 2

Lời giải:

+ Phương trình đường thẳng BC:

⇒ Phương trình BC: 3(x - 1) + 1(y + 2) = 0 hay 3x + y - 1 = 0 .

+ ta có; BC = 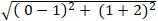 = √10

+ Xét vị trí tương đối giữa đường thẳng d và BC:

Ta có: 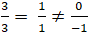 ⇒ d // BC.

Mà điểm A thuộc d nên d( A; BC) = d( d; BC) . (1)

+ Ta tính khoảng cách hai đường thẳng d và BC.

Lấy điểm O(0; 0) thuộc d.

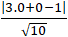
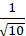
⇒ d(d; BC) = d(O;BC) =  =  ( 2)

Từ ( 1) và ( 2) suy ra d( A; BC) =  .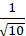

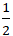
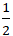
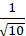
+ Diện tích tam giác ABC là S =  d( A,BC).BC =  . .√10 = 0, 5

Chọn C.

Bài 9: Cho hai đường thẳng d: x + y - 4 = 0 và đường thẳng ∆: 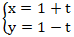 . Tính khoảng cách giữa hai đường thẳng này?

A. 1                        B. 2                           C. √2                                   D. Đáp án khác

Lời giải:

Đáp án: C

+Đường thẳng ∆: 

⇒ Phương trình đường thẳng ∆: 1( x - 1) + 1( y - 1) = 0 hay x + y - 2 = 0.

+ Ta có: 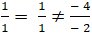 nên hai đường thẳng d//∆.

+ Lấy điểm A( 1; 1) thuộc ∆. Do d // ∆ nên :

d(d; ∆) = d(A; d) = 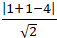 = √2

Bài 10: Cho đường thẳng d: x - 2y + 2 = 0 . Phương trình các đường thẳng song song với d và cách d một đoạn bằng √5 là

A. x - 2y - 3 = 0; x - 2y + 7 = 0    

B. x - 2y + 3 = 0 và x - 2y + 7 = 0

C. x - 2y - 3 = 0; x - 2y - 7 = 0    

D. x - 2y + 3 = 0; x - 2y - 7 = 0 .

Lời giải:

Đáp án: A

+ Gọi ∆ là đường thẳng song song với d: x - 2y + 2 = 0

⇒ Đường thẳng ∆ có dạng: x - 2y + c = 0 ( c ≠ 2 ) .

+ Lấy một điểm A( -2 ; 0) thuộc d.

⇒ d( d ; ∆) = d( A ; ∆) = √5

⇔  = √5 ⇔ |c - 2| = 5 nên 

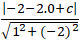
+ Vậy có hai đường thẳng thỏa mãn là x - 2y + 7 = 0 hoặc x - 2y - 3 = 0.

Bài 11: Cho đường thẳng d: 3x + 4y + 1 = 0. Có 2 đường thẳng d₁ và d₂ cùng song song với d và cách d một khoảng bằng 1. Hai đường thẳng đó có phương trình là:

A. 3x + 4y - 7 = 0; 3x - 4y + 3 = 0.    

B. 3x - 4y + 7 = 0; 3x - 4y - 3 = 0

C. 3x + 4y + 4 = 0; 3x + 4y + 3 = 0.    

D. 3x + 4y - 4 = 0; 3x + 4y + 6 = 0 .

Lời giải:

Đáp án: D

+ Do đường thẳng song song với d nên ∆ có dạng là : ∆ : 3x + 4y + c = 0 ( c ≠ 1) .

Lấy điểm M(-3 ; 2) thuộc d

Do d(d ; ∆) = d( M ; ∆) =1 ⇔ 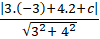 = 1

⇔ |c - 1| = 5 ⇔ 

Vậy có hai đường thẳng thỏa mãn là : 3x + 4y + 6 = 0 hoặc 3x + 4y - 4 = 0

Bài 12: Khoảng cách giữa 2 đường thẳng (a): 7x + y - 3 = 0 và (b): 7x + y + 12 = 0 là

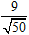
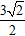
A.                              B. 9.                            C.                              D. 15.

Lời giải:

Đáp án: C

Ta có : 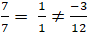 nên a // b

Lây điểm M (0 ; 3) thuộc( a) .

Do a // b nên d(M ; b) = d( a ; b) = 

Bài 13: Cho đường thẳng d: 3x - 4y + 2 = 0. Có đường thẳng a và b cùng song song với d và cách d một khoảng bằng 1. Hai đường thẳng đó có phương trình là:

A. 3x + 4y - 1 = 0 ; 3x + 4y + 5 = 0    

B. 3x - 4y + 7 = 0 ; 3x - 4y - 3 = 0

C. 3x + 4y - 3 = 0 ; 3x + 4y + 7 = 0    

 D. 3x - 4y + 6 = 0; 3x - 4y - 4 = 0

Lời giải:

Đáp án: B

Giả sử đường thẳng ∆ song song với d : 3x - 4y + 2 = 0

Khi đó ; ∆ có phương trình là ∆ : 3x - 4y + C = 0.

Lấy điểm M( -2 ; -1) thuộc d.

Do d(d; ∆) = 1 ⇔ 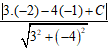 = 1 ⇔ |C - 2| = 5 ⇔ 

Do đó hai đường thẳng thỏa mãn là : 3x - 4y + 7 = 0 và 3x - 4y - 3 = 0.

Bài 14: Cho đường thẳng d: 2x - 3y + 6 = 0 và đường thẳng ∆: 4x - 6y + 20 = 0. Viết phương trình đường thẳng d’ // d sao cho khoảng cách hai đường thẳng d’ và ∆ là √13

A. 2x - 3y + 23 = 0    

B. 2x - 3y - 3 = 0.

C. 2x - 3y – 8 = 0 và 2x - 3y = 0    

D. Cả A và B đúng

Lời giải:

Đáp án: D

+ Ta có đường thẳng d’// d nên đường thẳng d’ có dạng : 2x - 3y + c = 0 ( c ≠ 6)

+ Xét vị trí của hai đường thẳng d và ∆: 

⇒ Hai đường thẳng d và ∆ song song với nhau .

Mà d // d’ nên d’ // ∆.

+ Lấy điểm A( -5; 0) thuộc ∆.

+ Do d’ // ∆ nên d( d’; ∆) = d( A; d’) = √13

⇔  = √13 ⇔ 

⇔ 

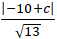
Vậy có hai đường thẳng thỏa mãn là 2x - 3y + 23 = 0 và 2x - 3y - 3 = 0.

Bài 15: Cho tam giác ABC có B( - 2; 1) và C( 2; 0). Điểm A thuộc đường thẳng
d: x+ 4y- 10= 0 .Tính diện tích tam giác ABC.

A. 1                       B. 3                         C. 0,5                                D. 2

Lời giải:

Đáp án: A

+ Phương trình đường thẳng BC:

⇒ Phương trình BC: 1( x + 2) + 4( y - 1) = 0 hay x + 4y - 2 = 0 .

+ ta có; BC = 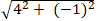 = √17

+ Xét vị trí tương đối giữa đường thẳng d và BC:

Ta có: 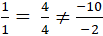 ⇒ d // BC.

Mà điểm A thuộc d nên d( A; BC) = d( d; BC) . (1)

+ Ta tính khoảng cách hai đường thẳng d và BC.

Lấy điểm H( 10; 0) thuộc d.

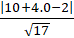
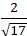
⇒ d(d; BC) = d(H;BC) =  =  ( 2)

Từ ( 1) và ( 2) suy ra d( A; BC) = 

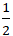
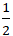
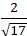
+ Diện tích tam giác ABC là S =  d( A,BC).BC =  .  .√17= 1

Bài 16: Cho hai đường thẳng song song là d: 6x + 8y + 9 = 0 và d’: 6x + 8y + 7 = 0. Tìm khoảng cách giữa d và d’.

Bài 17: Cho hai đường thẳng song song là d: x + y + 2 = 0 và d’: x + y + 5 = 0. Tìm khoảng cách giữa d và d’.

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

150 Bài tập phương trình đường thẳng (2024) có đáp án

80 Bài tập về vectơ trong mặt phẳng tọa độ (có đáp án năm 2024)

90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2024)

80 Bài tập Tổng và hiệu của hai vectơ (có đáp án năm 2024)

90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2024)