80 Bài tập về vectơ trong mặt phẳng tọa độ (có đáp án năm 2024)

Bài tập về vectơ trong mặt phẳng tọa độ

Kiến thức cần nhớ

1. Tọa độ của vectơ

– Trục tọa độ (còn gọi là trục, hay trục số) là một đường thẳng mà trên đó đã xác định một điểm O và một vectơ $\overrightarrow{i}$ có độ dài bằng 1. Điểm O gọi là gốc tọa độ, vectơ $\overrightarrow{i}$ gọi là vectơ đơn vị của trục. Điểm M trên trục biểu diễn số x₀ nếu $\overrightarrow{OM}=x_0\overrightarrow{i}$

– Trên mặt phẳng với một đơn vị đo độ dài cho trước, xét hai trục Ox, Oy có chung gốc O và vuông góc với nhau. Kí hiệu vectơ đơn vị của trục Ox là $\overrightarrow{i}$, vectơ đơn vị của trục Oy là $\overrightarrow{j}$. Hệ gồm hai trục Ox, Oy như vậy được gọi là hệ trục tọa độ Oxy. Điểm O gọi là gốc tọa độ, trục Ox gọi là trục hoành, trục Oy gọi là trục tung. Mặt phẳng chứa hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy hay mặt phẳng Oxy.

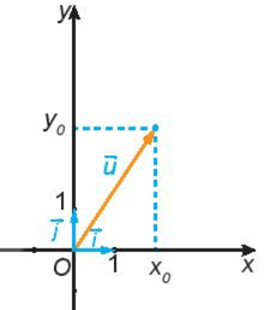
– Mỗi vectơ $\overrightarrow{u}$ trên mặt phẳng Oxy, có duy nhất cặp số (x₀; y₀) sao cho $\overrightarrow{u}=x_0\overrightarrow{i}+y_0\overrightarrow{j}$.

Ta nói vectơ $\overrightarrow{u}$ có tọa độ (x₀; y₀) và viết $\overrightarrow{u}$ = (x₀; y₀) hay $\overrightarrow{u}$(x₀; y₀). Các số x₀, y₀ tương ứng được gọi là hoành độ, tung độ của $\overrightarrow{u}$.

– Hai vectơ bằng nhau khi và chỉ khi chúng có cùng tọa độ.

$\overrightarrow{u}(x;y)=\overrightarrow{v}(x\text{'};y\text{'})\iff \left(\begin{array}{c}x=x\text{'}\\ y=y\text{'}.\end{array}\right)$

Ví dụ 1 : Trong mặt phẳng tọa độ Oxy, $\overrightarrow{u}$ = (2; –4). Hãy biểu diễn vectơ $\overrightarrow{u}$ qua vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

Hướng dẫn giải

Vì $\overrightarrow{u}$ = (2; –4) nên $\overrightarrow{u}=2\overrightarrow{i}+(-4)\overrightarrow{j}=2\overrightarrow{i}-4\overrightarrow{j}$

Vậy $\overrightarrow{u}=2\overrightarrow{i}-4\overrightarrow{j}$.

2. Biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ $\overrightarrow{u}$ = (x; y) và $\overrightarrow{v}$ = (x’; y’). Khi đó:

$\overrightarrow{u}$ + $\overrightarrow{v}$ = (x + x’ ; y + y’) ;

$\overrightarrow{u}$ – $\overrightarrow{v}$ = (x – x’ ; y – y’) ;

k $\overrightarrow{u}$ = (kx ; ky) với k ∈ℝ.

Ví dụ 2 : Cho $\overrightarrow{u}$ = (2; 3), = (–1; 2).

a) Tìm tọa độ của $\overrightarrow{u}$ + $\overrightarrow{v}$; $\overrightarrow{u}$ – $\overrightarrow{v}$.

b) Tìm tọa độ của vectơ 4$\overrightarrow{u}$.

Hướng dẫn giải

a) Ta có:

$\overrightarrow{u}$ + $\overrightarrow{v}$ = (2 + (–1); 3 + 2) = (1; 5)

$\overrightarrow{u}$ – $\overrightarrow{v}$ = (2 – (–1); 3 – 2) = (3; 1).

Vậy $\overrightarrow{u}$ + $\overrightarrow{v}$ = (1; 5) ; $\overrightarrow{u}$ – $\overrightarrow{v}$ = (3; 1).

b) 4$\overrightarrow{u}$ = (4.2 ; 4.3) = (8; 12)

Vậy 4$\overrightarrow{u}$ = (8; 12).

Nhận xét:

– Vectơ $\overrightarrow{v}$(x’; y’) cùng phương với vectơ $\overrightarrow{u}$(x; y) ≠ $\overrightarrow{0}$ khi và chỉ khai tồn tại số k sao cho x’ = kx, y’ = ky (hay là $\frac{x\text{'}}{x}=\frac{y\text{'}}{y}$ nếu xy ≠ 0).

– Nếu điểm M có tọa độ (x; y) thì vectơ $\overrightarrow{OM}$ có tọa độ (x; y) và độ dài $\left|\overrightarrow{OM}\right|=\sqrt{x^2+y^2}$.

– Với vectơ $\overrightarrow{u}$ = (x; y), ta lấy điểm M(x; y) thì $\overrightarrow{u}$ = $\overrightarrow{OM}$. Do đó $\left|\overrightarrow{u}\right|=\left|\overrightarrow{OM}\right|=\sqrt{x^2+y^2}$.

– Với hai điểm M(x; y) và N(x’ ; y’) thì và khoảng cách giữa hai điểm M, N là MN = $\left|\overrightarrow{MN}\right|=\sqrt{{(x\text{'}-x)}^2+{(y\text{'}-y)}^2}$.

Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1; –2), B(3; 2), C(7; 4).

a) Tìm tọa độ của các vectơ $\overrightarrow{AB},\overrightarrow{BC}$.

b) So sánh các khoảng cách từ B tới A và C.

c) Ba điểm A, B, C có thẳng hàng không?

Hướng dẫn giải

a) Ta có $\overrightarrow{AB}=(3-1;2-(-2\left)\right)=(2;4)$;

$\overrightarrow{BC}=(7-3;4-2)=(4;2).$

b) Các khoảng cách từ B đến A và C lần lượt là:

AB = $\left|\overrightarrow{AB}\right|=\sqrt{2^2+4^2}=\sqrt{20}=2\sqrt{5}$;

BC = $\left|\overrightarrow{BC}\right|=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}$.

Suy ra AB = BC = $2\sqrt{5}$.

Vậy khoảng cách từ B đến A bằng khoảng cách từ B đến C.

c) Hai vectơ $\overrightarrow{AB}=(2;4)$ và $\overrightarrow{BC}=(4;2)$ không cùng phương (vì $\frac{2}{4}\ne \frac{4}{2}$).

Do đó các điểm A, B, C không cùng nằm trên cùng một đường thẳng.

Vậy ba điểm A, B, C không thẳng hàng.

Chú ý:

- Trung điểm M của đoạn thẳng AB có tọa độ là $\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)$.

- Trọng tâm G của tam giác ABC có tọa độ là $\left(\frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3}\right)$.

Các dạng bài tập về vectơ trong mặt phẳng tọa độ

Dạng 1. Tìm tọa độ điểm, tọa độ vectơ trên mặt phẳng Oxy.

Dạng 2. Xác định tọa độ điểm, vectơ liên quan đến biểu thức dạng u + v, u – v, ku.

Dạng 3. Xác định tọa độ các điểm của một hình.

Dạng 4. Bài toán liên quan đến sự cùng phương của hai vectơ. Phân tích một vectơ qua hai vectơ không cùng phương.

Bài tập có hướng dẫn

1. Bài tập vận dụng

1.1. Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.

A. M(1; 2);

B. M(-1; 2);

C. M(1; -2);

D. M(-1; -2)

Hướng dẫn giải

Đáp án đúng là A

Ta có hai vecto $\overrightarrow{OA}\left(2;1\right),\overrightarrow{OB}\left(3;3\right)$  không cùng phương (vì $\frac{2}{3}\ne \frac{1}{3}$ ). Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.

Suy ra các điểm O, A, B không thẳng hàng

Để OABM là hình bình hành khi và chỉ khi $\overrightarrow{OA}=\overrightarrow{MB}$

Ta có: $\overrightarrow{OA}\left(2;1\right),\overrightarrow{MB}\left(3-x;3-y\right)$  nên $\left\{\begin{array}{l}2=3-x\\ 1=3-y\end{array}\right.\iff \left\{\begin{array}{l}x=1\\ y=2\end{array}\right.\Rightarrow M\left(1;2\right).$

Vậy điểm cần tìm là M(1;2).

Câu 2. Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài $\overrightarrow{BC}$  là:

A. 5;

B. 3;

C. $\sqrt{13}$ ;

D. $\sqrt{15}$ .

Hướng dẫn giải

Đáp án đúng là C

Ta có $\overrightarrow{BC}$  = (3 – 1; -1 – 2) = (2; -3).

$\Rightarrow \left|\overrightarrow{BC}\right|=\sqrt{2^2+{\left(-3\right)}^2}=\sqrt{13}.$

Câu 3. Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.

A. Tam giác OMN là tam giác đều;

B. Tam giác OMN vuông cân tại M;

C. Tam giác OMN vuông cân tại N;

D. Tam giác OMN vuông cân tại O.

Hướng dẫn giải

Đáp án đúng là B

Ta có M(1;3) $\Rightarrow \overrightarrow{OM}\left(1;3\right)\Rightarrow OM=\sqrt{1^2+3^2}=\sqrt{10}.$

Ta lại có N(4;2) $\Rightarrow \overrightarrow{ON}\left(4;2\right)$$\Rightarrow ON=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}.$

$\Rightarrow \overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=\left(-3;1\right)$$\Rightarrow MN=\sqrt{{\left(-3\right)}^2+1^2}=\sqrt{10}$

Xét tam giác OMN, có: $OM=MN=\sqrt{10}$  nên tam giác OMN cân tại M.

Ta có: $O{N}^2={\left(2\sqrt{5}\right)}^2=20,$ $O{M}^2+M{N}^2={\left(\sqrt{10}\right)}^2+{\left(\sqrt{10}\right)}^2=20$

$\Rightarrow O{N}^2=O{M}^2+M{N}^2$

Theo định lí Py – ta – go đảo suy ra tam giác OMN vuông tại O.

Do đó tam giác OMN vuông cân tại M.

1.2. Bài tập tự luận

Câu 4: Cho $\overrightarrow{u}=(3;-2)$ và $\overrightarrow{v}=(7;4)$. Tìm tọa độ của các vectơ $\overrightarrow{u}+\overrightarrow{v}$, $\overrightarrow{u}-\overrightarrow{v}$, $3\overrightarrow{u}-4\overrightarrow{v}$ .

Hướng dẫn giải

Ta có $\overrightarrow{u}+\overrightarrow{v}$ = (3 + 7; (–2) + 4) = (10; 2)

$\overrightarrow{u}-\overrightarrow{v}$ = (3 – 7 ; (–2) – 4) = (–4 ;–6)

$3\overrightarrow{u}=(3.3;3.(-2\left)\right)=(9;-6)$

$4\overrightarrow{v}=(4.7;\text{4.4) = (28;16)}$

Suy ra: $3\overrightarrow{u}-4\overrightarrow{v}=(9-28;(-6)-16)=(-19;-22)$.

Vậy: $\overrightarrow{u}+\overrightarrow{v}$ = (10 ; 2) ; $\overrightarrow{u}-\overrightarrow{v}$ =(4 ;– 6) ; $3\overrightarrow{u}-4\overrightarrow{v}=(-19;-22)$.

Câu 5: Trong mặt phẳng tọa độ Oxy cho các điểm A(1; –2) và B(2; 1).

a) Tính độ dài các đoạn thẳng OA, OB.

b) Tam giác OAB là tam giác gì? Vì sao?

Hướng dẫn giải

a) Ta có $\overrightarrow{OA}=(1;-2)\Rightarrow \left|\overrightarrow{OA}\right|=\sqrt{1^2+{(-2)}^2}=\sqrt{5}$.

Suy ra OA = $\left|\overrightarrow{OA}\right|=\sqrt{5}$

Ta có $\overrightarrow{OB}=(2;1)\Rightarrow \left|\overrightarrow{OB}\right|=\sqrt{2^2+1^2}=\sqrt{5}$.

Suy ra OB = $\left|\overrightarrow{OB}\right|=\sqrt{5}$

Vậy OA = $\sqrt{5}$; OB = $\sqrt{5}$.

b) Ta có: $\overrightarrow{AB}=\left(1;3\right)$ nên $AB=\left(\overrightarrow{AB}\right)=\sqrt{1^2+3^2}=\sqrt{10}$.

Xét tam giác OAB có OA = OB nên tam giác OAB là tam giác cân tại O.

Vậy tam giác OAB cân tại O.

Câu 6: Cho hình bình hành ABCD có A(–1; 3), B(2; 4), C(0; 1). Tìm tọa độ đỉnh D.

Hướng dẫn giải

Giả sử D(x; y), khi đó $\overrightarrow{AD}=(x+1;y-3)$; $\overrightarrow{BC}=(0-2;1-4)=(-2;-3)$.

Vì ABCD là hình bình hành nên ta có: $\overrightarrow{AD}=\overrightarrow{BC}$. Do đó:

$\left(\begin{array}{c}x+1=-2\\ y-3=-3\end{array}\right)\iff \left(\begin{array}{c}x=-3\\ y=0\end{array}\right)$

Vậy tọa độ điểm D(–3 ; 0).

2. Bài tập tự luyện có hướng dẫn

(Xem thêm các bài tập trong file pdf)

Xem thêm các dạng bài tập liên quan khác:

90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2023)

80 Bài tập số gần đúng và sai số (có đáp án năm 2023)

80 Bài tập về Tích vô hướng của một vectơ với một số (có đáp án năm 2023)

80 Bài tập Tổng và hiệu của hai vectơ (có đáp án năm 2023)

90 Bài tập các khái niệm mở đầu (có đáp án năm 2023)