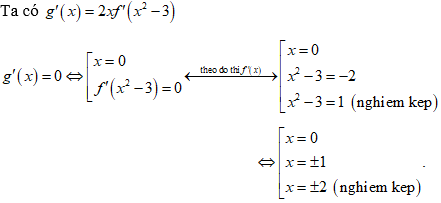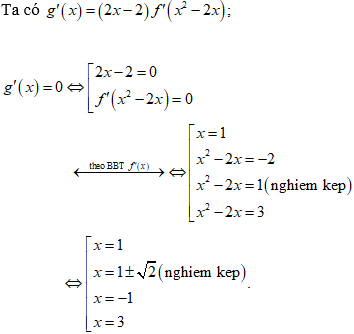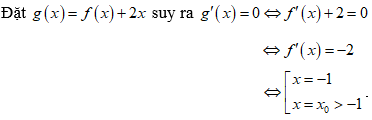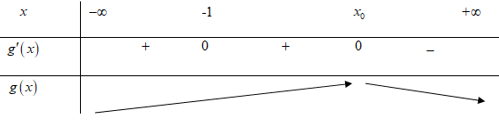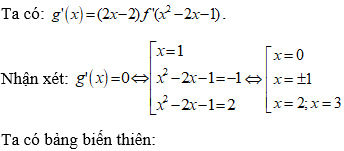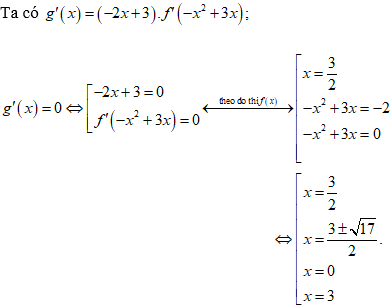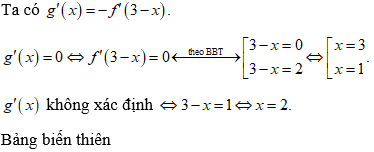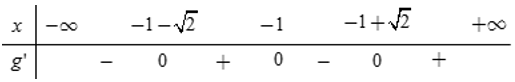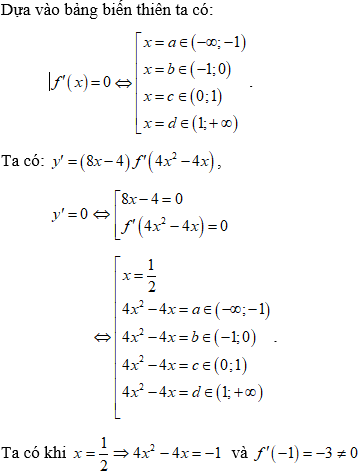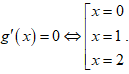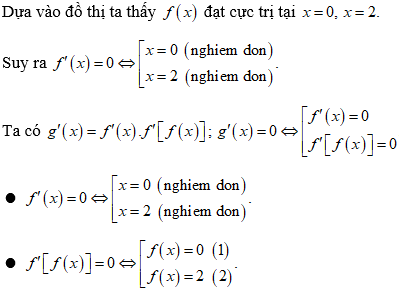20 Bài tập tìm cực trị của hàm hợp (2024) cực hay, có đáp án

Cách tìm cực trị của hàm hợp

1. Phương pháp giải

a. Kiến thức cần nhớ

- Đạo hàm của hàm hợp:

  [f(u(x))]' = u'(x).f'(u(x))

- Tính chất đổi dấu của biểu thức:

Gọi x = α là một nghiệm của phương trình: f(x) = 0. Khi đó

+) Nếu x = α là nghiệm bội bậc chẳn ((x - α)²,(x - α)⁴,...) thì hàm số y = f(x) không đổi dấu khi đi qua α.

+) Nếu x = α là nghiệm đơn hoặc nghiệm bội bậc lẻ ((x - α),(x - α)³,...) thì hàm số y = f(x) đổi dấu khi đi qua α.

b. Phương pháp

Đề tìm cực trị của hàm số y = f(u(x)) ta làm như sau:

- Bước 1: Tính [f(u(x))]'

- Bước 2: Giải phương trình [f(u(x))]' = 0 dựa vào đồ thị hay bảng biến thiên của hàm số y = f(x)

- Bước 3: Lập bảng biến thiên của hàm số

- Bước 4: Kết luận về các điểm cực trị

2. Ví dụ minh họa

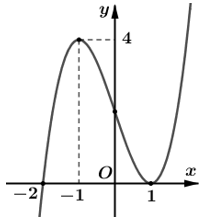
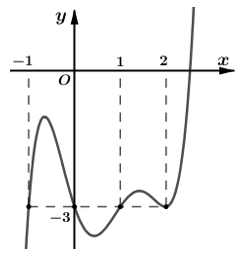
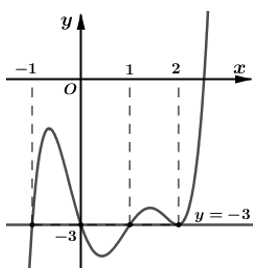
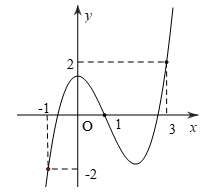
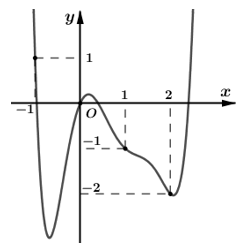
Ví dụ 1: Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình bên.

Tìm số điểm cực trị của hàm số g(x) = f(x² - 3).

A. 2.

B. 3

C. 4.

D. 5.

Lời giải

Chọn B

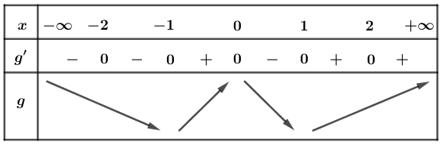
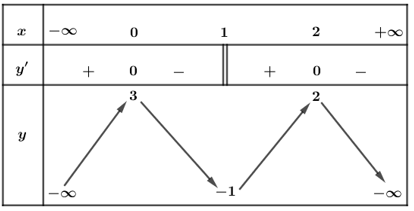
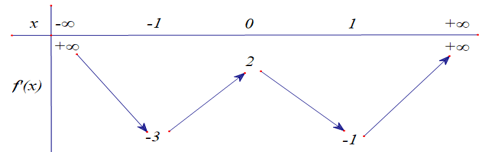
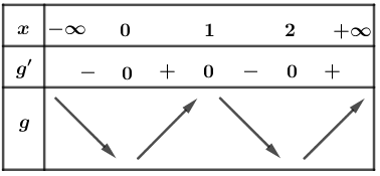
Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.

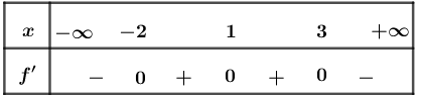
Ví dụ 2: Cho hàm số y = f(x) có đạo hàm trên R và có bảng xét dấu của y = f'(x) như sau

Hỏi hàm số g(x) = f(x² - 2x) có bao nhiêu điểm cực tiểu ?

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải

Chọn A

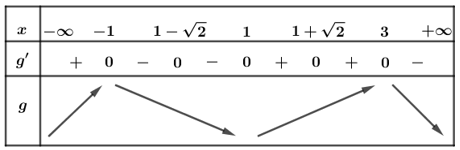
Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có một điểm cực tiểu.

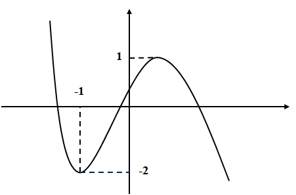
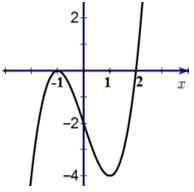
Ví dụ 3: Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f'(x) như hình vẽ sau. Số điểm cực trị của hàm số y = f(x) + 2x là:

A. 4.

B. 1.

C. 3.

D. 2.

Lời giải

Chọn B

Dựa vào đồ thị ta có: Trên (-∞;-1) thì f'(x) > -2 ⇔ f'(x) + 2 > 0.

Trên (-1;x₀) thì f'(x) > -2 ⇔ f'(x) + 2 > 0.

Trên (x₀;+∞) thì f'(x) < -2 ⇔ f'(x) + 2 < 0.

Bảng biến thiên của hàm g(x)

Vậy hàm số g(x) = f(x) + 2x có 1 cực trị.

3. Bài tập vận dụng (có đáp án)

Bài 1: Cho hàm số y = f(x) có đạo hàm f'(x) trên R và đồ thị của hàm số f'(x) như hình vẽ.

Tìm số điểm cực trụ hàm số g(x) = f(x² - 2x - 1).

A. 6

B. 5.

C. 4.

D. 3.

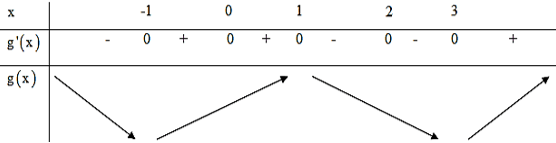
Lời giải:

Chọn D

Dựa vào bảng biến thiên, ta thấy hàm số có đúng ba cực trị.

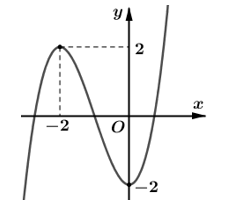
Bài 2: Cho hàm số y = f(x) có đồ thị hàm số như hình bên.

Hàm số g(x) = f(-x² + 3x) có bao nhiêu điểm cực đại?

A. 3.

B. 4

C. 5.

D. 6.

Lời giải:

Chọn C

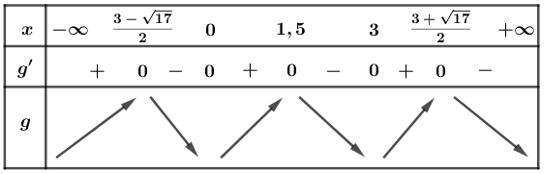
Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có 5 điểm cực trị.

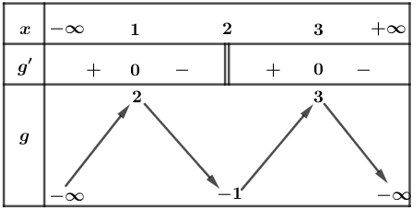
Bài 3: Cho hàm số y = f(x) có bảng biến thiên như sau

Tìm số điểm cực trị của hàm số g(x) = f(3 - x).

A. 2.

B. 3.

C. 5.

D. 6.

Lời giải:

Chọn B

Vậy hàm số g(x) = f(3 - x) có 3 điểm cực trị.

Bài 4: Cho hàm số y = f(x) có đạo hàm trên R Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x) = f(x) + 3x có bao nhiểu điểm cực trị ?

A. 2.

B. 3.

C. 4.

D. 7.

Lời giải:

Chọn B

Ta có g'(x) = f'(x) + 3; g'(x) = 0 ⇔ f'(x) = -3.

Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và đường thẳng y = -3.

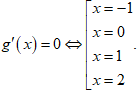
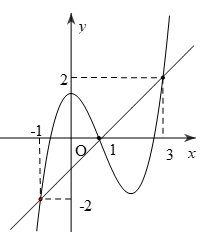
Dựa vào đồ thị ta suy ra  Ta thấy x = -1, x = 0, x = 1 là các nghiệm đơn và x = 2 là nghiệm kép nên đồ thị hàm số g(x) = f(x) + 3x có 3 điểm cực trị

Bài 5: Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị của hàm số y = f'(x) như hình vẽ.

Tìm số điểm cực trị của hàm số g(x) = 2f(x) - x² + 2x + 2017.

A. 2.

B. 3.

C. 4.

D. 7.

Lời giải:

Chọn B

Ta có g'(x) = 2f'(x)-2x + 2 = 2[f'(x)-(x-1)].

Dựa vào hình vẽ ta thấy đường thẳng y = x-1 cắt đồ thị hàm số y = f'(x) tại 3 điểm: (-1;-2), (1;0), (3;2).

Dựa vào đồ thị ta có

 đều là các nghiệm đơn

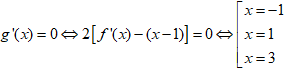
Vậy hàm số y = g(x) có 3 điểm cực trị.

Bài 6: Cho hàm số bậc bốn y = f(x). Đồ thị hình bên dưới là đồ thị của đạo hàm f'(x). Hàm số 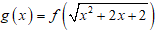 có bao nhiêu điểm cực trị ?

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải:

Chọn C

 đều là các nghiệm đơn

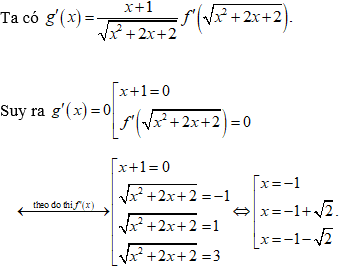
Bảng xét dấu

Từ đó suy ra hàm số 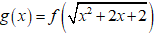 có 3 điểm cực trị.

Bài 7: Cho hàm số f(x), bảng biến thiên của hàm số f'(x) như sau:

Số điểm cực trị của hàm số y = f(4x² - 4x) là

A. 9.

B. 5.

C. 7.

D. 3.

Lời giải:

Chọn B

Vậy phương trình y' = 0 có 7 nghiệm bội lẻ phân biệt nên hàm số có 7 điểm cực trị.

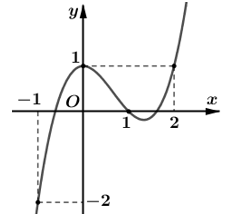
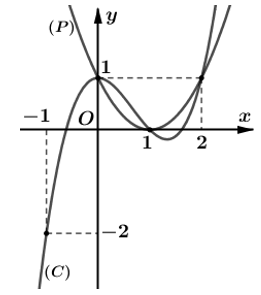
Bài 8: Cho hàm số y = f(x) có đạo hàm trên R Đồ thị hàm số y = f'(x) như hình vẽ bên dưới.

Hàm số 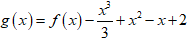 đạt cực đại tại:

A. x = -1.

B. x = 0.

C. x = 1.

D. x = 2.

Lời giải:

Chọn C

Ta có g'(x) = f'(x) - x² + 2x - 1; g'(x) = 0 ⇔ f'(x) = (x - 1)².

Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và parapol (P): y = (x-1)².

Dựa vào đồ thị ta suy ra 

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy g(x) đạt cực đại tại x = 1.

Bài 9: Cho hàm số y = f(x) có đạo hàm trên R Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. Hàm số g(x) = 2f(x)+x² đạt cực tiểu tại điểm

A. x = -1.

B. x = 0.

C. x = 1.

D. x = 2.

Lời giải:

Chọn B

Ta có g'(x) = 2f'(x) + 2x; g'(x) = 0 ⇔ f'(x) = -x.

Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và đường thẳng y = -x.

Dựa vào đồ thị ta suy ra 

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy g(x) đạt cực tiểu tại x = 0.

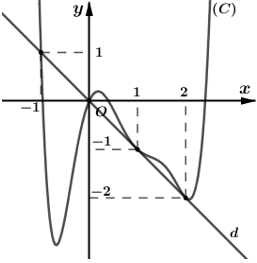
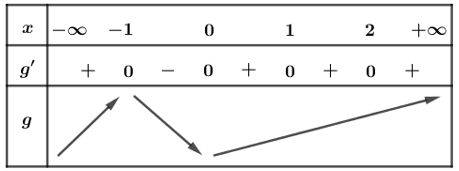
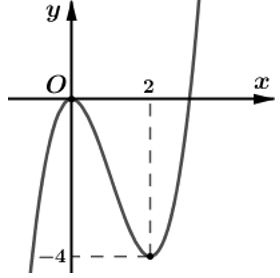
Bài 10: Cho hàm số y = f(x) có đồ thị như hình vẽ bên.

Hàm số g(x) = f[f(x)] có bao nhiêu điểm cực trị?

A. 3.

B. 5.

C. 4.

D. 6.

Lời giải:

Chọn C

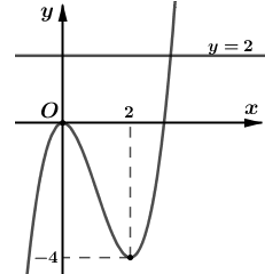
Dựa vào đồ thị suy ra:

● Phương trình (1) có hai nghiệm x = 0 (nghiệm kép) và x = a(a > 2).

● Phương trình (2) có một nghiệm x = b(b > a).

Vậy phương trình g'(x) = 0 có nghiệm bội lẻ là x = 0, x = 2, x = a và x = b. Suy ra hàm số g(x) = f[f(x)] có 4 điểm cực trị.

Xem thêm các dạng bài tập liên quan khác:

20 bài tập Tìm cực trị của hàm số dựa vào đồ thị (2024) cực hay, có lời giải

20 Bài tập Tìm cực trị của hàm chứa căn thức (2024) cực hay, có đáp án

20 Bài tập Tìm cực trị của hàm bậc ba (2024) cực hay, có lời giải

30 Bài tập Tìm cực trị của hàm chứa dấu giá trị tuyệt đối (2024) cực hay, có lời giải

20 Bài tập Tìm cực trị của hàm số dựa vào bảng biến thiên (2024) cực hay, có đáp án chi tiết nhất