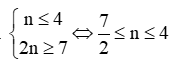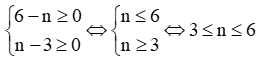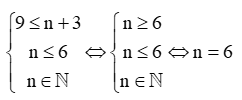Trắc nghiệm Toán 8 Bài 5: Phép chia đa thức cho đơn thức
A. Trắc nghiệm
Câu 1. Cho P =(75x5y2−45x4y3):(3x3y2)−(52x2y4−2xy5):(12xy3). Khẳng định nào sai?
A. P≥0,∀x, y≠0
B. P>0⇔5x−2y≠0
C. P =0⇔5x = 2y≠0
D. P nhận cả giá trị âm và dương.
Đáp án đúng là: B
P =(75x5y2−45x4y3):(3x3y2)−(52x2y4−2xy5):(12xy3)
P=25x2−15xy−5xy+4y2
P=25x2−20xy+4y2
P=(5x−2y)2
⇒P>0⇔5x−2y≠0
Câu 2. Cho đa thức B thỏa mãn (B+2x2y3).(−3xy)=−3x2y2−6x3y4. Đa thức B là
A. B = xy
B. B = – xy
C. B = x + 1
D. B = x2y
Đáp án đúng là: A
Ta có:
(B+2x2y3).(−3xy)=−3x2y2−6x3y4
⇒B+2x2y3=(−3x2y2−6x3y4):(−3xy)
⇒B+2x2y3=xy+2x2y3
⇒B=xy+2x2y3−2x2y3
⇒B=xy
Câu 3. Một cửa hàng buổi sáng bán được xy bao gạo thì của hàng đó thu được số tiền là x6y5−x5y4 nghìn đồng. Số tiền mỗi bao gạo của cửa hàng đó đã bán khi x = 2; y = 2 là
A. 384 nghìn đồng
B. 284 nghìn đồng
C. 120 nghìn đồng
D. 84 nghìn đồng
Đáp án đúng là: A
Số tiền mỗi bao gạo của cửa hàng đã bán theo x , y là:
(x6y5−x5y4): xy = x5y4−x4y3 (nghìn đồng)
Số tiền mỗi bao gạo mà cửa hàng đó đã bán khi x = 2; y =2 là:
25.24−24.23=384 (nghìn đồng)
Câu 4. Với giá trị tự nhiên nào của n thì phép chia (14x8y4−9x2ny6):(−2x7yn) là phép chia hết?
A. 72≤n≤4
B. n = 4
C. n≥72
D. n≥4
Đáp án đúng là: B
Để (14x8y4−9x2ny6):(−2x7yn) là phép chia hết thì
Mà n là số tự nhiên nên n = 4.
Câu 5. Cho A = x5yn – 12xn+1y4; B = 24xn-1y3. Số tự nhiên n > 0 để A ⋮ B là
A. n ∈ {3;4;5;6}
B. n ∈ {4;5;6}
C. n ∈ {1;2;3;4;5;6}
D. n ∈ {4;5}
Đáp án đúng là: A
A:B=(x5yn−12xn+1y4):(24xn−1y3)
=x5yn:24xn−1y3−12xn+1y4:24xn−1y3
=124x6−nyn−3−12x2y
Để A⋮B thì
Mà n là số tự nhiên nên n ∈ {3;4;5;6}.
Câu 6. Giá trị của số tự nhiên thỏa mãn điều kiện gì để phép chia xn+3y6:x9yn là phép chia hết?
A. n < 6
B. n = 5
C. n > 6
D. n = 6
Đáp án đúng là: D
Để phép chia xn+3y6:x9yn là phép chia hết:
Câu 7. Đa thức 7x3y2z−2x4y3 chia hết cho đơn thức nào dưới đây?
A. 3x4
B. −3x4
C. −2x3y
D. 2x3y
Đáp án đúng là: C
Đa thức 7x3y2z−2x4y3 chia hết cho đơn thức −2x3y
Câu 8. Thực hiện phép chia (2x4y−6x2y7):(2x2) ta được đa thức ax2y+by7 (a, b là hằng số). Khi đó a + b bằng
A. – 3.
B. – 4.
C. – 2.
D. – 5.
Đáp án đúng là: C
(2x4y−6x2y7):(2x2)=x2y−3y7 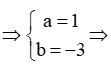
Câu 9. Giá trị của biểu thức P=[(3ab)2−9a2b4]:(8ab2) tại a=23;b=32 là
A. −2316
B. −258
C. −1516
D. −218
Đáp án đúng là: C
P=[(3ab)2−9a2b4]:(8ab2)
=9a2b2−9a2b4:(8ab2)
=98a−98ab2
Thay a=23;b=32vào biểu thức P ta có: P=98.23−98.23(32)2=−1516
Câu 10. Kết quả phép chia (6x4y+4x3y3−2xy):(xy) là một đa thức có bậc bằng
A. 3.
B. 4.
C. 7.
D. 9.
Đáp án đúng là: B
(6x4y+4x3y3−2xy):(xy)=6x3+4x2y2−2 là đa thức có bậc 4 .
Câu 11. Đa thức N thỏa mãn −15x6y5−20x4y4−25x5y3=(−5x3y2).N là:
A. N =−3x3y3+4xy2+5x2y
B. N =−3x2y3+4xy+5x2y
C. N = 3x3y3+4xy2+5x2y
D. N = 3x3y3+4xy2+5xy
Đáp án đúng là: C
−15x6y5−20x4y4−25x5y3=(−5x3y2).N
⇒N=(−15x6y5−20x4y4−25x5y3):(−5x3y2)
⇒N =3x3y3+4xy2+5x2y
Câu 12. Biểu thức D=(9x2y2−6x2y3):(−xy)2+(6x5y+2x4):(2x4) sau khi rút gọn là một đa thức có bậc bằng
A. 1.
B. 2.
C. 3.
D. 4.
Đáp án đúng là: B
D=(9x2y2−6x2y3):(−xy)2+(6x5y+2x4):(2x4)
D=(9x2y2−6x2y3):(9x2y2)+(6x5y+2x4):(2x4)
D=1−23y+3xy+1
D=2−23y+3xy
Vậy đa thức sau rút gọn có bậc là 2
Câu 13. Giá trị của biểu thức: A=[(x−y)5+(x−y)4+(x−y)3]:(x−y) với x = 3;
y = 4 là:
A. 28
B. 16
C. 20
D. 14
Đáp án đúng là: A
Ta có:
A=[(x−y)5+(x−y)4+(x−y)3]:(x−y)
A=(x−y)7+(x−y)3+(x−y)2
Với x = 3; y = 4 ta có
A=(3−1)4+(3−1)3+(3−1)2=24+23+22=28
Câu 14. Chọn kết luận đúng về biểu thức:
E =23x2y3:(−13xy)+ 2x(y−1)(y + 1)(x≠0; y≠0; y≠1)
A. Giá trị của biểu thức không phụ thuộc vào biến x.
B. Giá trị của biểu thức không phụ thuộc vào biến y.
C. Giá trị của biểu thức không phụ thuộc vào biến.
D. Giá trị của biểu thức bằng 0.
Đáp án đúng là: B
Ta có:
E =23x2y3:(−13xy)+ 2x(y−1)(y + 1)
E=−2xy3+2x[y(y+1)−1.(y+1)]
E=−2xy3+2x(y2−1)
E=−2xy3+2xy2−2x
E=−2x
Giá trị của biểu thức không phụ thuộc vào biến y.
Câu 15. Giá trị của biểu thức D =(15xy2+18xy3+16y2):6y2−7x4y3:x4y tại x=23;y=1 là
A. 283
B. 32
C. 23
D. -23
Đáp án đúng là: D
Ta có:
D =(15xy2+18xy3+16y2):6y2−7x4y3:x4y
D =15xy2:6y2+18xy3:6y2+16y2:6y2−7x4y3:x4y
D=52x+3xy+83−7y2
Tại x=23;y=1 ta có
D=52.23+3.23.1+83−7.12=53+2+83−7=133−5=−23
B. Lý thuyết
Sơ đồ tư duyToán 8 Bài 5: Phép chia đa thức cho đơn thức
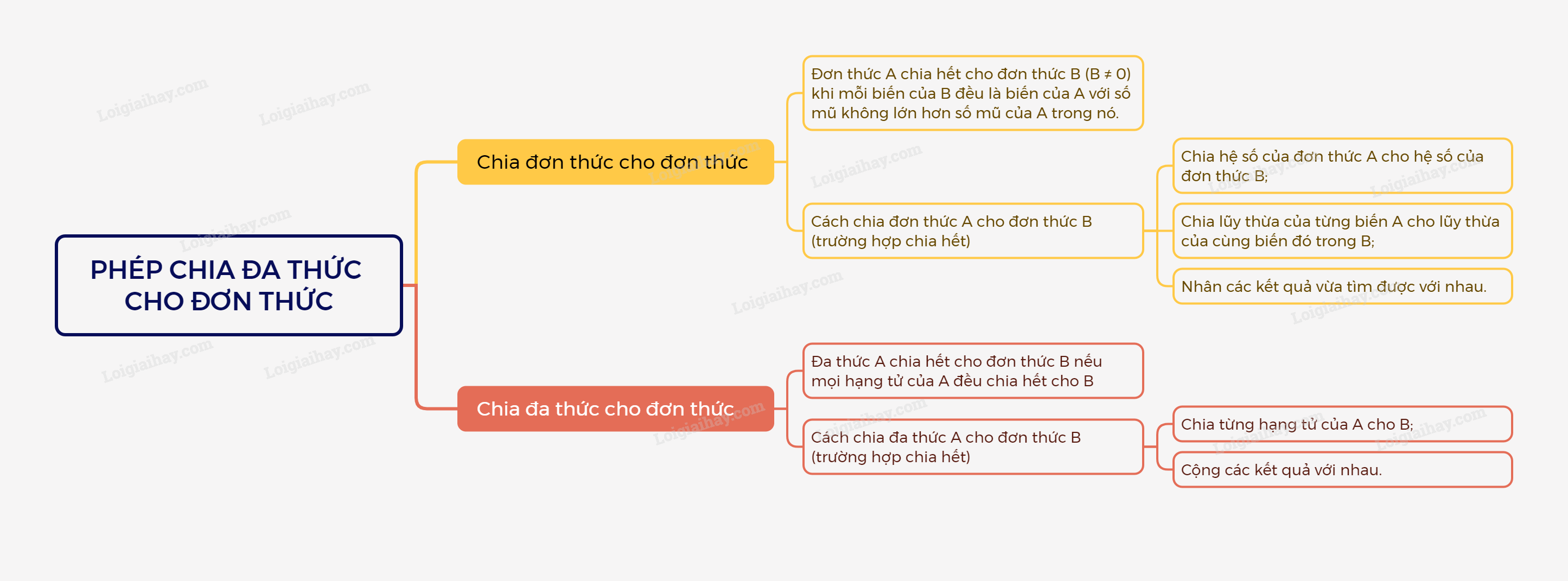
1. Chia đơn thức cho đơn thức như thế nào?
a. Đơn thức A chia hết cho đơn thức B(B≠0)khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
b. Muốn chia đơn thức A cho đơn thức B (trường hợp chia hết), ta làm như sau:
- Chia hệ số của đơn thức A cho hệ số của đơn thức B;
- Chia lũy thừa của từng biến A cho lũy thừa của cùng biến đó trong B;
- Nhân các kết quả vừa tìm được với nhau.
Ví dụ:
16x4y3:(−8x3y2)=(16:(−8)).(x4:x3).(y3:y2)=−2xy
2. Chia đa thức cho đơn thức như thế nào?
Đa thức A chia hết cho đơn thức B nếu mọi hạng tử của A đều chia hết cho B.
Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.
Ví dụ:
(x2y+y2x):xy=x2y:xy+y2x:xy=x+y
(−12x4y+4x3−8x2y2):(−4x2)=(−12x4y);(−4x2)+(4x3):(−4x2)−(8x2y2):(−4x2)=3x2y−x+2y2
Xem thêm các bài trắc nghiệm Toán 8 Kết nối tri thức hay, có đáp án khác:
Trắc nghiệm Bài 3: Phép cộng và phép trừ đa thức
Trắc nghiệm Bài 4: Phép nhân đa thức
Trắc nghiệm Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Trắc nghiệm Bài 7: Lập phương của một tổng. Lập phương của một hiệu