Trắc nghiệm Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu
A. Trắc nghiệm
Câu 1. Cho biết
Q=(2x−1)3−8x(x+1)(x−1)+2x(6x−5) =ax−b(a, b∈ℤ). Khi đó
A. a = – 4; b = 1
B. a = 4; b = – 1
C. a = 4; b = 1
D. a = – 4; b = – 1
Đáp án đúng là: C
Ta có
Q=(2x−1)3−8x(x+1)(x−1)+2x(6x−5) =ax−b(a, b∈ℤ)
=8x3−12x2+6x−1−8x(x2−1)+12x2−10
=8x3−12x2+6x−1−8x3+8x+12x2−10x
=4x−1
⇒a=4;b=1
Câu 2. Cho hai biểu thức P=(4x + 1)3−(4x + 3)(16x2+ 3);Q =(x−2)3−x(x + 1)(x−1)+ 6x(x−3)+ 5x. So sánh P và Q?
A. P < Q
B. P = –Q
C. P = Q
D. P > Q
Đáp án đúng là: C
Ta có
P =(4x + 1)3−(4x + 3)(16x2+ 3)
=(4x)3+3.(4x)2.1+3.4x.12+13−(64x3+12x+48x2+9)
=64x3+48x2+12x+1−64x3−12x−48x2−9
= - 8
Q =(x−2)3−x(x + 1)(x−1)+ 6x(x−3)+ 5x
=x3−3.x2.2+3x.22−23−x(x2−1)+6x2−18x+5x
=x3−6x2+12x−8−x3+x+6x2−18x+5x
= - 8
⇒P = Q
Câu 3. Cho 2x - y = 9. Giá trị của biểu thức
A=8x3−12x2y+6xy2−y3+12x2 −12xy+3y2+6x−3y+11 là
A. A = 1001
B. A = 1000
C. A = 1010
D. A = 900
Đáp án đúng là: C
Ta có
A=8x3−12x2y+6xy2−y3+12x2−12xy+3y2+6x−3y+11
=(2x)3−3.(2x)2.y+3.2x.y+y3+3(4x2−4xy+y2)+3(2x−y)+11
=(2x−y)3+3(2x−y)2+3(2x−y)+1+10
=(2x−y+1)3+10
Thay 2x - y = 9 vào biểu thức A ta có A=(9+1)3+10=1010
Câu 4. Giá trị của biểu thức Q=a3−b3 biết a - b = 4 và ab = -3 là
A. Q = 100
B. Q = 64
C. Q = 28
D. Q = 36
Đáp án đúng là: C
Ta có
(a−b)3=a3−3a2b+3ab2−b3=a3−b3−3ab(a−b)
⇒a3−b3=(a−b)3+3ab(a−b)
⇔Q=(a−b)3+3ab(a−b)
Thay a + b = 5 và ab = − 3 vào Q ta có
Q=(a−b)3+3ab(a−b)
=43+3.(−3).4
= 64 - 36 = 28
Câu 5. Cho a + b + c = 0 . Giá trị của biểu thức B=a3+b3+c3−3abc
A. B = 0
B. B = 1
C. B = – 1
D. Không xác định được.
Đáp án đúng là: A
(a+b)3=a3+3a2b+3ab2+b3=a3+b3+3ab(a+b)
⇒a3+b3=(a+b)3−3ab(a+b)
Ta có
B=a3+b3+c3−3abc
=(a+b)3−3ab(a+b)+c3−3abc
=(a+b)3+x3−3ab(a+b+c)
Tương tự, ta có (a+b+c)3−3(a+b)c(c+b+c)
⇔B=(a+b+c)3−3(a+b)c(a+b+c)−3ab(a+b+c)
Mà a + b + c = 0 nên B = 0−3(a + b)c.0−3ab.0 = 0.
Câu 6. Chọn câu đúng?
A. (A + B)3= A3+ 3A2B + 3AB2+ B3
B. (A−B)3=A3−3A2B−3AB2−B3
C. (A + B)3= A3+ B3
D. (A−B)3= A3−B3
Đáp án đúng là: A
(A + B)3= A3+ 3A2B + 3AB2+ B3
Câu 7. Viết biểu thức x3+3x2+3x+1 dưới dạng lập phương của một tổng
A. (x+1)3
B. (x+3)3
C. (x−1)3
D. (x−3)3
Đáp án đúng là: A
x3+ 3x2+ 3x+ 1 =(x + 1)3
Câu 8. Khai triển hằng đẳng thức (x−2)3 ta được
A. x3−6x2+ 12x−8
B. x3+ 6x2+ 12x + 8
C. x3−6x2−12x−8
D. x3+ 6x2−12x+8
Đáp án đúng là: A
(x−2)3= x3−3.x2.2 + 3.x.22−23= x3−6x2+ 12x−8
Câu 9. Cho A +34x2−32x + 1 =(B + 1)3. Khi đó
A. A =−x38; B =x2
B. A =−x38; B =−x2
C. A =−x38; B =−x8
D. A =x38; B =x8
Đáp án đúng là: B
=(−12x)3+3.(−12x)2.1+3.(−12x).12+13
=(−x2+1)3
⇒A=(−12x)3=−x38;B=−12x=−x2
Vậy P là một số chẵn.
Câu 10. Viết biểu thức 8 − 36x + 54x2−27x3 dưới dạng lập phương của một tổng hoặc một hiệu ta được
A. (3x+2)3
B. (2−3x)3
C. (8−27x)3
D. (3x−2)3
Đáp án đúng là: B
8 − 36x + 54x2−27x3=23−3.2
Câu 11. Kết quả phép nhân:
A.
B. ;
C. ;
D.
Đáp án đúng là: C
Ta có:
Câu 12. Cho biểu thức
. Khi đó
A. H là một số chia hết cho 12.
B. H là một số chẵn.
C. H là một số lẻ.
D. H là một số chính phương.
Đáp án đúng là: C
= 117
Vậy H là một số lẻ.
Câu 13. Tính giá trị của biểu thức tại x = 20, y = 1
A. 4000
B. 6000
C. 8000
D. 2000
Đáp án đúng là: C
Thay x = 20, y = 1 vào biểu thức M ta có
Câu 14. Cho hai biểu thức
Tìm mối quan hệ giữa hai biểu thức P, Q?
A. P = – Q
B. P = 2Q
C. P = Q
D.
Đáp án đúng là: C
= – 8
= - 8
P = Q
Câu 15. Rút gọn biểu thức
ta được
A.
B.
C.
D.
Đáp án đúng là: C
B. Lý thuyết
Sơ đồ tư duy Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu
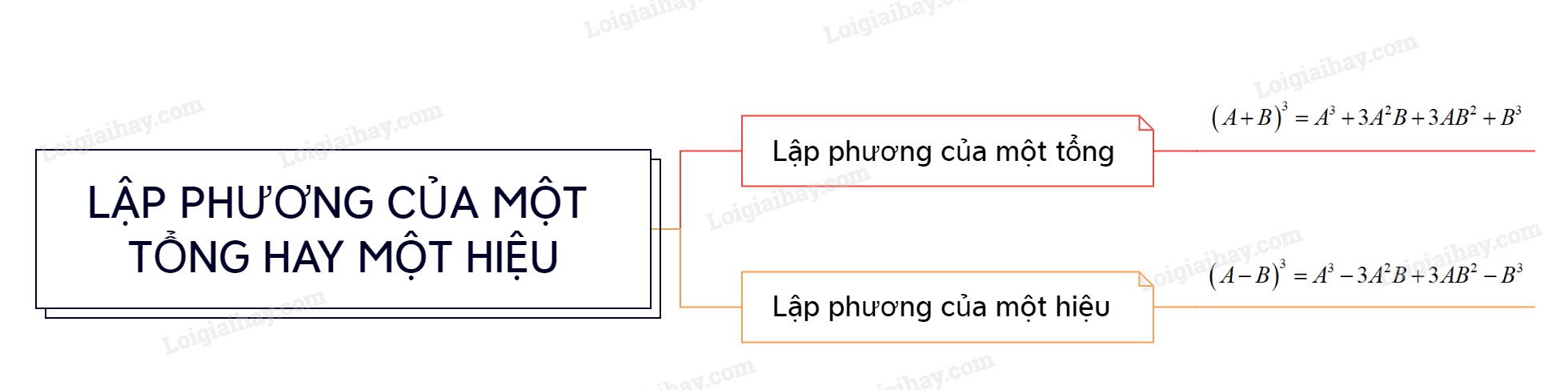
Lập phương của một tổng:
Ví dụ:
Lập phương của một hiệu:
Ví dụ:
Xem thêm các bài trắc nghiệm Toán 8 Kết nối tri thức hay, có đáp án khác:
Trắc nghiệm Bài 5: Phép chia đa thức cho đơn thức
Trắc nghiệm Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Trắc nghiệm Bài 8: Tổng và hiệu hai lập phương




