Trắc nghiệm Toán 8 Bài 4: Phép nhân đa thức
A. Trắc nghiệm
Câu 1. Biểu thức D=x(x2n−1+y)−y(x+y2n−1)+y2n−x2n+5 có giá trị là
A. 2y2n
B. −5
C. x2n
D. 5
Đáp án đúng là: D
Ta có: D=x(x2n−1+y)−y(x+y2n−1)+y2n−x2n+5
=x.x2n−1+x.y−y.x−y.y2n−1+y2n−x2n+5
=x2n+xy−xy−y2n+y2n−x2n+5
=(x2n−x2n)+(xy−xy)+(y2n−y2n)+5
Câu 2. Cho hình thang có đáy lớn gấp đôi đáy nhỏ, đáy nhỏ lớn hơn chiều cao 2 đơn vị. Biểu thức tính diện tích hình thang là
A. S=3x2−6x
B. S=3x2−6x2
C. S=x2+2x+42
D. S=x2−2x−42
Đáp án đúng là: B
Gọi x(x>2) là độ dài đáy nhỏ của hình thang
Theo giả thiết ta có độ dài đáy lón là 2x, chiều cao của hình thang là x - 2
Diện tích hình thang là:
S=(x+2x)(x−2)2=3x(x−2)2=3x2−6x2 (dddt).
Câu 3. Cho biết (x+y)(x+z)+(y+z)(y+x) =2(z+x)(z+y). Khi đó
A. z2=x2+y22
B. z2=x2+y2
C. z2=2(x2+y2)
D. z2=x2−y2
Đáp án đúng là: A
Ta có
(x+y)(x+z)+(y+z)(y+x)=2(z+x)(z+y)
x.x.xz+yx+yz+y.y+yx+zy+zx=2(z.z+zy+zx+xy)
x2+2xz+2xy+2yx+y2 = =2z2+2zy+2xz+2xy
x2+2xz+2xy+2yz+y2−2z2−2zy−2xz−2xy=0
x2+y2−2z2=0⇔x2+y2=2z2
z2=x2+y22
Câu 4. Cho m số mà mỗi số bằng 3n – 1 và n số mà mỗi số bằng 9 – 3m. Biết tổng tất cả các số đó bằng 5 lần tổng m + n. Khi đó
A. m=23n
B. m = n
C. m = 2n
D. m=32n
Đáp án đúng là: A
+ Tổng của m số mà mỗi số bằng 3n – 1 là m(3n – 1)
+ Tổng của n số mà mỗi số bằng 9 – 3m là n(9 – 3m)
Tổng tất cả các số trên là m(3n – 1) + n(9 – 3m)
Theo đề bài ta có
m(3n – 1) + n(9 – 3m) = 5(m + n)
Suy ra 3mn – m + 9n – 3mn = 5m + 5n
Do đó 6m = 4n nên m=23n
Câu 5. Cho các số x, y, z tỉ lệ với các số a, b, c. Khi đó (x2+2y2+3z2)(a2+2b2+3c2) bằng
A. ax+2by+3cz
B. (2ax+by+3cz)2
C. (2ax+3by+cz)2
D. (ax+2by+3cz)2
Đáp án đúng là: D
Vì x;y;z tỉ lệ với các số a;b;c nên xa=yb=zc=k suy ra x = ka, y = kb, z = kc
Thay x = ka, y = kb, z = kc vào (x2+2y2+3z2)(a2+2b2+3c2) ta được
((ka)2)(+2(kb)2+3(kc)2)(a2+2b2+3c2)
=(k2a2+2k2b2+3k2c2)(a2+2b2+3c2)
=k2(a2+2b2+3c2)(a2+2b2+3c2)
=k2(a2+2b2+3c2)2=(k(a2+2b2+3c2))2
=(ka2+2kb2+3kc2)2
=(ka.a+2kb.b+3kc.c)2
=(xa+2yb+3zc)2 do x = ka, y = kb, z = kc
Vậy (x2+2y2+3z2)(a2+2b2+3c2)=(ax+2by+3cz)2
Câu 6. Tích (−5x)2y2⋅15xy bằng
A. 5x3y3
B. −5x3y3
C. −x3y3
D. x3y2
Đáp án đúng là: A
Ta có:
(−5x)2y2.15xy=(−5)2.x2.15xy=25.15.(x2.x)(y2.y)=5x3y3
Câu 7. Tích 4a3y.(3xy−y+14) có kết quả bằng
A. 12x4y2−4x3y+x3y
B. 12x4y2−4x3y2+14x3y
C. 12x3y2+4x3y2+4x3y
D. 12x4y2−4x3y2+x3y
Đáp án đúng là: D
Ta có: 4a3y.(3xy−y+14)
=4x3y.3xy−4x3y.y+4x3y⋅14
=12x4y2−4x3y2+x3y
Câu 8. Giá trị của biểu thức P=−2x2y(xy+y2) tại x=−1;y=2 là
A. 8
B. −8
C. 6
D. −6
Đáp án đúng là: B
Thay x=−1;y=2 vào biểu thức P=−2x2y(xy+y2) ta được
P=−2.(−1)2.2[(−1).2+22]=−4.2
Câu 9. Tích có kết quả bằng
A.
B.
C.
D.
Đáp án đúng là: C
Ta có
Câu 10. Chọn câu sai? Giá trị của biểu thức
A. tại là .
B. tại là .
C. tại là 0 .
D. tại x = 5; y = - 5 là 0 .
Đáp án đúng là: B
+) Thay x = 1; y = 0 vào biểu thức ta được
nên phương án A đúng
+) Thay x = 0; y = 1 vào biểu thức ta được
a. nên phương án B sai.
+) Thay x = - 5; y = - 5 vào biểu thức ta được
nên phương án C đúng
+) Thay x = 5; y = - 5 vào biểu thức ta được
nên phương án D đúng.
Câu 11. Thực hiện phép tính nhân ta được kết quả
A.
B.
C.
D.
Đáp án đúng là: C
Ta có:
Câu 12. Giá trị của biểu thức tại x = – 1; y = 10 là
A. – 1001
B. 1001
C. 999
D. −999
Đáp án đúng là: C
Ta có:
Tại x = – 1; y = 10 thì giá trị biểu thức là:
Câu 13. Kết quả rút gọn biểu thức là
A. 3
B. 0
C. – 1
D. 1
Đáp án đúng là: C
= - 1
Câu 14. Cho biểu thức . Chọn khẳng định đúng.
A. Biểu thức C không phụ thuộc vào x;y;z
B. Biểu thức C phụ thuộc vào cả x;y;z
C. Biểu thức C chỉ phụ thuộc vào y
D. Biểu thức C chỉ phụ thuộc vào z
Đáp án đúng là: A
Ta có:
Nên C không phụ thuộc vào x;y;z.
Câu 15. Cho , đẳng thức nào sau đây đúng?
A. 2(x + 1)(y + 1) = (x + y)(x + y – 2)
B. 2(x + 1)(y + 1) = (x + y)(x + y + 2)
C. 2(x + 1)(y + 1) = x + y
D. (x + 1)(y + 1) = (x + y)(x + y + 2)
Đáp án đúng là: B
Ta có 2(x + 1)(y + 1) = 2(xy + x + y + 1) = 2xy + 2x + 2y + 2
Thay x2 + y2 = 2 ta được
= x(x + y + 2) + y(x + y + 2)
= (x + y)(x + y +2)
Từ đó ta có 2(x + 1)(y + 1) = (x + y)(x + y + 2)
B. Lý thuyết
Sơ đồ tư duyToán 8 Bài 4: Phép nhân đa thức
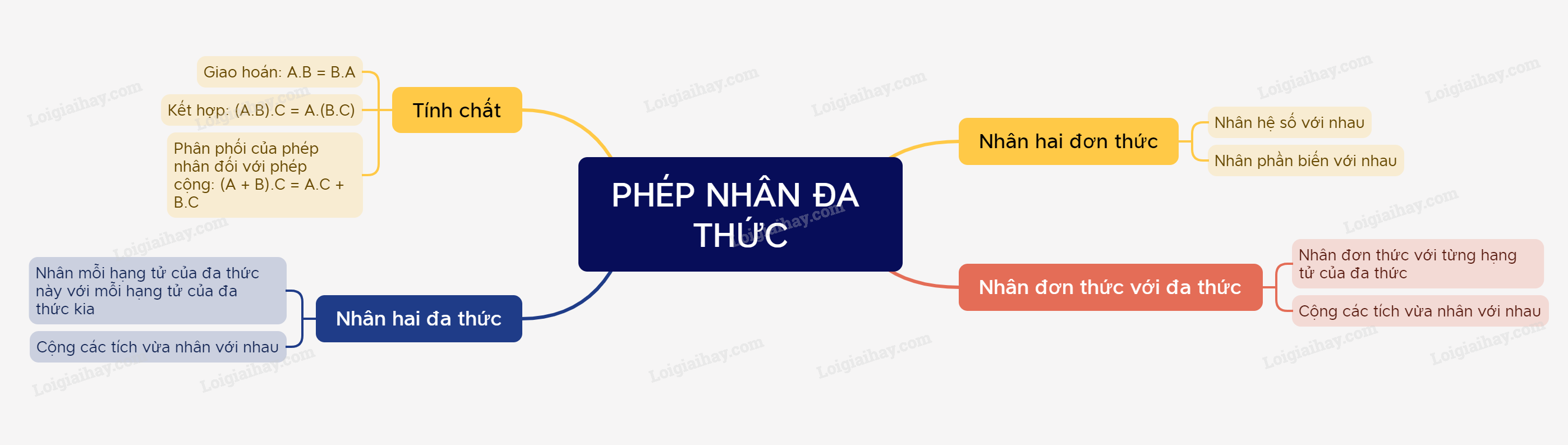
1. Nhân đơn thức với đa thức
+ Nhân hai đơn thức như thế nào?
Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau.
Ví dụ:
+ Nhân đơn thức với đa thức như thế nào?
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
Ví dụ:
2. Nhân đa thức với đa thức
+ Nhân hai đa thức như thế nào?
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Phép nhân đa thức cũng có các tính chất tương tự phép nhân các số.
+ Giao hoán: A.B = B.A
+ Kết hợp: (A.B).C = A.(B.C)
+ Phân phối của phép nhân đối với phép cộng: (A + B).C = AB + AC
Ví dụ:
Xem thêm các bài trắc nghiệm Toán 8 Kết nối tri thức hay, có đáp án khác:
Trắc nghiệm Bài 3: Phép cộng và phép trừ đa thức
Trắc nghiệm Bài 5: Phép chia đa thức cho đơn thức
Trắc nghiệm Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Trắc nghiệm Bài 7: Lập phương của một tổng. Lập phương của một hiệu




