Trắc nghiệm Toán 8 Bài 2: Đa thức
A. Trắc nghiệm
Câu 1. Cho x thỏa mãn điều kiện (2x2+7)(x+2)=0(2x2+7)(x+2)=0. Giá trị của đa thức x3−3x+1x3−3x+1 là
A. 10
B. 1
C. – 1
D. 11
Đáp án đúng là: C
Vì 2x2+7>02x2+7>0 với mọi x nên từ (2x2+7)(x+2)=0(2x2+7)(x+2)=0 ta suy ra x + 2 = 0 do đó x = -2
Thay x = – 2 vào biểu thức x3−3x+1x3−3x+1 ta được: (−2)3−3.(−2)+1=−1(−2)3−3.(−2)+1=−1
Câu 2. Cho Q=5xn+2+3xn+2xn+2+4xn+xn+2+xn(n∈ℕ). Giá trị của x để Q = 0 là
A. 0
B. 1
C. – 1
D. 0 và 1
Đáp án đúng là: A
Ta có:
Q=5xn+2+3xn+2xn+2+4xn+xn+2+xn(n∈ℕ)
Q=8xn+2+8xn=8xn(x2+1)
Vì x2+1>0 với mọi x nên Q = 0 ta có 8xn(x2+1)=0, suy ra x = 0.
Vậy x = 0 thì Q = 0
Câu 3. Giá trị của đa thức Q = x2y3+2x2+4 như thế nào khi x < 0, y > 0?
A. Q = 0
B. Q > 0
C. Q < 0
D. Không xác định được
Đáp án đúng là: B
Vì x < 0, y > 0 nên:
x2y3>0
2x2>0
4 > 0
Suy ra Q = x2y3+2x2+4>0
Câu 4. Cho đa thức 4x5y2−5x3y+7x3y+2ax5y2. Giá trị của a để bậc đa thức bằng 4 là
A. a = 2
B. a = 0
C. a = – 2
D. a = 1
Đáp án đúng là: C
Ta có:
4x5y2−5x3y+7x3y+7x3y
=(4x5y2+2ax5y2)+(−5x3y+7x3y)
=(4+2a)x5y2+2x3y
Để bậc của đa thức đã cho bằng 4 thì 4+2a=0⇔a=−2
Câu 5. Cho x2+ y2= 2. Giá trị của đa thức 3x4+5x2y2+2y4+2y2 là
A. 6
B. 8
C. 12
D. 0
Đáp án đúng là: C
Ta có:
3x4+5x2y2+2y4+2y2
=(3x4+3x2y2)+(2x2y2+2y4+2y2)
=(x2+y2)+2y2(x2+y2+1)
Mà x2+y2=2 nên ta có:
3x2(x2+y2)+2y2(x2+y2+1)=6x2+6y2=6(x2+y2)=6.2=12
Câu 6. Bậc của đa thức x2y5−x2y4+y6+1 là
A. 4.
B. 5.
C. 6.
D. 7.
Đáp án đúng là: D
Ta có:
x2y5 có bậc là 7.
x2y4 có bậc là 6
y6 có bậc là 6
1 có bậc là 0
Vậy đa thức x2y5−x2y4+y6+1 có bậc là 7
Câu 7. Cho đa thức: Q(x)=8x5+2x3−7x+1. Các hệ số khác 0 của đa thức Q(x) là
A. 5; 3; 1.
B. 8; 2; –7.
C. 13; 4; – 6; 1.
D. 8; 2; –7; 1.
Đáp án cần chọn là: D
Đa thức: Q(x)=8x5+2x3−7x+1 có các hệ số khác 0 là 8; 2; –7; 1.
Câu 8. Giá trị của biểu thức 2x3y2−7x3y2+5x3y2+8x3y2 tại x = – 1; y = 1 bằng
A. 8
B. – 8
C. – 13
D. 10
Đáp án đúng là: B
Ta có: 2x3y2−7x3y2+5x3y2+8x3y2=8x3y2
Thay x = – 1; y = 1 vào biểu thức 8x3y2 ta có −8.(−1)3.12=−8
Câu 9. Sắp xếp các hạng tử của P(x)=2x3−5x2+x4−7 theo lũy thừa giảm dần của biến.
A. P(x)=x4+2x3−5x2−7
B. P(x)=5x2+2x3+x4−7
C. P(x)=−7−5x2+2x3+x4
D. P(x)=7−5x2+2x3+x4
Đáp án đúng là: A
Ta có: P(x)=2x3−5x2+x4−7=x4+2x3−5x2−7
Câu 10. Thu gọn đa thức M=−3x2y−7xy2+3x2y+5xy2 được kết quả là
A. M=6x2y−12xy2
B. M=12xy2
C. M=−2xy2
D. M=−6x2y−2xy2
Đáp án đúng là: C
Ta có:
M=−3x2y−7xy2+3x2y+5xy2
=(−3x2y+3x2y)+(−7xy2+5xy2)=−2xy2
Câu 11. Tính (5x2−3x+9)−(2x2−3x+7) ta được kết quả là
A. 7x2−6x+16
B. 3x2+2
C. 3x2+6x+16
D. 7x2+2
Đáp án đúng là: B
(5x2−3x+9)−(2x2−3x+7)
=5x2−3x+9−2x2+3x−7=3x2+2
Câu 12. Cho A = 3x3y2+2x2y−xy và B=4xy−3x2y+2x3y2+y2. Đa thức M = A + B là
A. M=5x3y−x2y−3xy+y2
B. M=5x3y2+5x2y+3xy+y2
C. M=5x3y2+5x2y−3xy+y2
D. M=5x3y−x2y+3xy+y2
Đáp án đúng là: D
A+B=3x3y2+2x2y−xy+4xy−3x2y+2x3y2+y2
=(3x3y2+2x3y2)+(−2x2y−3x2y)+(−xy+4xy)+y2
=5x3y2−x2y+3xy−y2
Câu 13. Cho P+(2x2+6xy−5y2)=3x2−6xy−5y2. Đa thức P là
A. P = x2−12xy
B. P=x2+10y2
C. P=−x2−12xy+10y2
D. P=12xy+10y2
Đáp án đúng là: A
Ta có
P+(2x2+6xy−5y2)=3x2−6xy−5y2
P=3x2−6xy−5y2−2x2−6xy+5y2
P=x2−12xy
Câu 14. Bậc của đa thức (x2+y2−2xy)−(x2+y2+2xy)+(4xy−1) là
A. 2
B. 1
C. 3
D. 0
Đáp án đúng là: D
Ta có:
(x2+y2−2xy)−(x2+y2+2xy)+(4xy−1)
=x2+y2−2xy−x2+y2+2xy+4xy−1
=(x2−x2)+(y2−y2)+(−4xy+4xy)−1=−1
Bậc của đa thức –1 là 0.
Câu 15. Tính giá trị của đa thức Q = 3x4+2y4−3z2+4 theo x biết y=x;z=x2 ta được kết quả là
A. Q=3x4
B. Q=3x4−4
C. Q=−3x4−4
D. Q=2x4+4
Đáp án đúng là: D
Thay y=x;z=x2 vào đa thức Q ta được:
Q = 3x4+2y4−3z2+4=3x4+2x4−3x4+4=2x4+4
B. Lý thuyết
Sơ đồ tư duy Toán 8 Bài 2: Đa thức
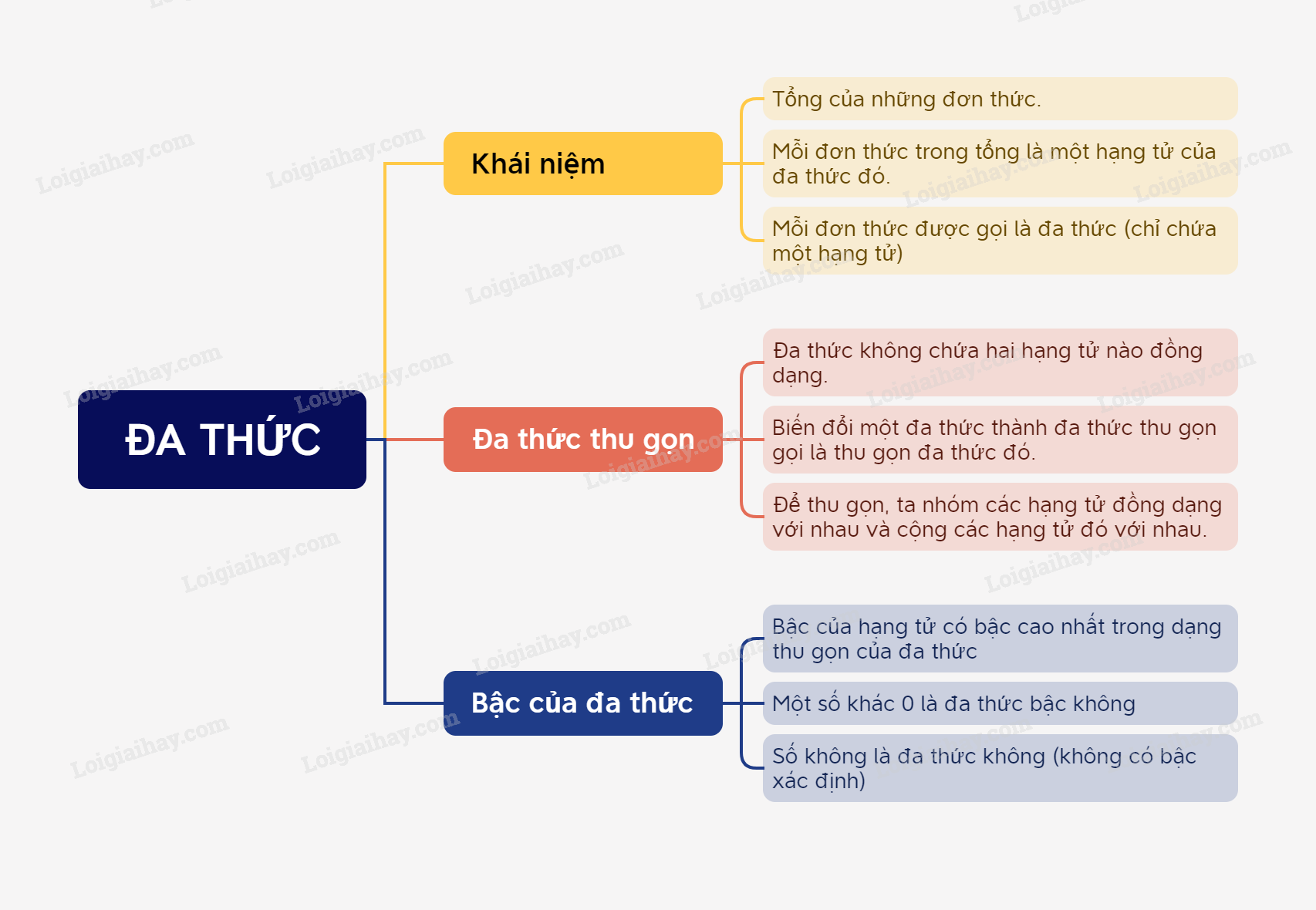
1. Đa thức
Đa thức là một tổng của những đơn thức.
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ: x2−4x+3;x2+3xyz2−yz+1;(x+3y)+(2x−−y) là đa thức.
x+yx−y,x2+2x2−y2 không phải là đa thức.
x2−4x+3 có 3 hạng tử x2;−4x;3.
x2+3xyz2−yz+1 có 4 hạng tử x2;3xyz2;−yz;1.
2. Đa thức thu gọn
Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Ví dụ:
A=x3−2x2y−x2y+3xy2−y3=x3−3x2y−3xy2−y3
3. Bậc của đa thức
Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Một số khác 0 tùy ý được coi là một đa thức bậc 0.
Số 0 cũng là một đa thức, gọi là đa thức không. Nó không có bậc xác định.
Xem thêm các bài trắc nghiệm Toán 8 Kết nối tri thức hay, có đáp án khác:
Trắc nghiệm Bài 3: Phép cộng và phép trừ đa thức
Trắc nghiệm Bài 4: Phép nhân đa thức
Trắc nghiệm Bài 5: Phép chia đa thức cho đơn thức
Trắc nghiệm Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu




