TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 1: Đơn thức

1900.edu.vn xin giới thiệu Bộ trắc nghiệm Toán 8 Bài 1: Đơn thức sách Kết nối tri thức hay, có đáp án sẽ giúp học sinh dễ dàng ôn tập kiến thức Toán 8 Bài 1. Mời các bạn đón xem:

Trắc nghiệm Toán 8 Bài 1: Đơn thức

A. Trắc nghiệm

Câu 1. Kết quả sau khi thu gọn biểu thức đại số $9 {(x^{2} y^{2})}^{4} x - {(- 2 xy)}^{3} x^{2} y + 3 {(2 x)}^{4} {xy}^{4}$ là

A. $59 x^{5} y^{4}$

B. $49 x^{5} y^{4}$

C. $65 x^{5} y^{4}$

D. $17 x^{5} y^{4}$

Hiển thị đáp án

Đáp án đúng là: C

Ta có:

$9 {(x^{2} y^{2})}^{4} x - {(- 2 xy)}^{3} x^{2} y + 3 {(2 x)}^{4} {xy}^{4}$

$= 9 {(x^{2})}^{2} {(y^{2})}^{2} x - {(- 2)}^{3} x^{3} y^{3} x^{2} y + 3 {.2}^{4} x^{4} {xy}^{4}$

$= 9 x^{4} y^{4} x - (- 8) x^{3} y^{3} x^{2} y + 48 x^{4} {xy}^{4}$

$= 9 x^{5} y^{4} + 8 x^{5} y^{4} + 48 x^{5} y^{4}$

$= (9 + 8 + 48) x^{5} y^{4} = 65 x^{5} y^{4}$

Câu 2. Xác định hằng số a để các đơn thức ${axy}^{3}, - 4 {xy}^{3}, 7 {xy}^{3}$ có tổng bằng $6 {xy}^{3}$

A. a = 9

B. a = 1

C. a = 3

D. a = 3

Hiển thị đáp án

Đáp án đúng là: C

Ta có: ${axy}^{3} + (- 4 {xy}^{3}) + 7 {xy}^{3} = (a - 4 + 7) {xy}^{3}$

Từ giả thiết suy ra: $a + 3 = 6 \Leftrightarrow a = 6 - 3 \Leftrightarrow a = 3$

Câu 3. Kết quả sau khi thu gọn đơn thức $1 \frac{1}{4} x^{2} y (- \frac{6}{5} xy) (- 2 \frac{1}{3} xy)$ là

A. $\frac{7}{2} x^{4} y^{3}$

B. $\frac{1}{2} x^{3} y^{3}$

C. $- \frac{7}{2} x^{4} y^{3}$

D. $- \frac{1}{2} x^{2} y^{2}$

Hiển thị đáp án

Đáp án đúng là: A

Ta có:

$1 \frac{1}{4} x^{2} y (- \frac{6}{5} xy) (- 2 \frac{1}{3} xy) = [\frac{5}{4} . (- \frac{6}{5}) . (\frac{- 7}{3})] (x^{2} . x . x) . (y . y . y) = \frac{7}{2} x^{4} y^{3}$

Câu 4. Cho các biểu thức $A = 4 x^{3} y (- 5 xy), B = - 17 x^{4} y^{2}$ . Đa thức A.B là

A. $74 x^{8} y^{4}$

B. $740 x^{4} y^{2}$

C. $- 740 x^{8} y^{4}$

D. $340 x^{8} y^{4}$

Hiển thị đáp án

Đáp án đúng là: D

$4 x^{3} y (- 5 x y) . (- 17 x^{4} y^{2}) = (4) . (- 5) . (- 17) . (x^{3} . x . x^{4}) (y . y . y^{2}) = 340 x^{8} y^{4}$

Câu 5. Cho đơn thức $A = (2 a^{2} + \frac{1}{a^{2}}) x^{2} y^{4} z^{6} (a \neq 0)$ . Chọn khẳng định đúng:

A. Giá trị của A luôn không âm với mọi x, y, z.

B. Nếu A = 0 thì x = y = z = 0

C. Chỉ có 1 giá trị của x để A = 0

D. Chỉ có 1 giá trị của y để A = 0

Hiển thị đáp án

Đáp án đúng là: A

$A = (2 a^{2} + \frac{1}{a^{2}}) x^{2} y^{4} z^{6} (a \neq 0)$

Ta có: $2 a^{2} + \frac{1}{a^{2}} > 0$ với $a \neq 0$

Lại có: $x^{2} \geq 0; y^{4} \geq 0; z^{6} \geq 0 \Rightarrow x^{2} y^{4} z^{6} \geq 0$ với mọi x; y; z.

Câu 6. Trong các biểu thức sau, biểu thức nào là đơn thức?

A. $2 + x^{2} y$

B. $- \frac{1}{5} x^{4} y^{5}$

C. $\frac{x + y^{3}}{3 y}$

D. $- \frac{3}{4} x^{3} y + 7 x$

Hiển thị đáp án

Đáp án đúng là: B

Theo định nghĩa đơn thức, biểu thức $- \frac{1}{5} x^{4} y^{5}$ là đơn thức.

Câu 7. Đơn thức ${−3x}^{2} y^{3}$ có hệ số là

A. $- 3 x^{3} y^{2}$

B. $3 x^{2} y^{3}$

C. 3

D. -3

Hiển thị đáp án

Đáp án đúng là: D

Đơn thức $- 3 x^{2} y^{3}$ có hệ số là −3.

Câu 8. Có mấy nhóm đơn thức đồng dạng với nhau trong các đơn thức sau?

$− \frac{2}{3} x^{3} y; - {xy}^{2}; 5 x^{2} y; 6 {xy}^{2}; 2 x^{3} y; \frac{3}{4}; \frac{1}{2} x^{2} y$

A. 2

B. 3

C. 4

D. 5

Hiển thị đáp án

Đáp án đúng là: B

Có ba nhóm đơn thức đồng dạng trong các đơn thức đã cho gồm:

Nhóm thứ nhất: $- \frac{2}{3} x^{3} y; 2 x^{3} y$

Nhóm thứ hai: $5 x^{2} y; \frac{1}{2} x^{2} y$

Nhóm thứ ba: $- {xy}^{2}; 6 {xy}^{2}$

Câu 9. Các đơn thức $- 10; \frac{1}{3} x; 2 x^{2} y; 5 x^{2} . x^{2}$ có bậc lần lượt là

A. 0; 1; 3; 4

B. 0; 3; 1; 4

C. 0; 1; 2; 3

D. 0; 1; 3; 2

Hiển thị đáp án

Đáp án đúng là: A

Đơn thức – 10 có bậc là 0.

Đơn thức $\frac{1}{3} x$ có bậc là 1.

Đơn thức $2 x^{2} y$ có bậc là 2 + 1 = 3

Đơn thức $5 x^{2} . x^{2} = 5 x^{4}$ có bậc là 4.

Các đơn thức $- 10; \frac{1}{3} x; 2 x^{2} y; 5 x^{2} . x^{2}$ có bậc lần lượt là: 0; 1; 3; 4.

Câu 10. Cặp đơn thức nào sau đây không đồng dạng với nhau?

A. $7 x^{3} y$ và $\frac{1}{15} x^{3} y$

B. $- \frac{1}{8} {(xy)}^{2} x^{2}$ và $32 x^{2} y^{3}$

C. $5 x^{2} y^{2}$ và $- 2 x^{2} y^{2}$

D. ${ax}^{2} y$ và $2 {bx}^{2} y$ (a, b là những số khác 0)

Hiển thị đáp án

Đáp án đúng là: B

Vì $- \frac{1}{8} {(xy)}^{2} x^{2} = - \frac{1}{8} x^{4} y^{2}$ không đồng dạng với đơn thức $32 x^{2} y^{3}$

Câu 11. Sau khi thu gọn đơn thức $2 . (- 3 x^{3} y) y^{2}$ ta được đơn thức:

A. $- 6 x^{3} y^{3}$

B. $6 x^{3} y^{3}$

C. $x^{3} y^{2}$

D. $- 6 x^{2} y^{3}$

Hiển thị đáp án

Đáp án đúng là: A

Ta có: $2 . (- 3 x^{3} y) y^{2} = 2 . (- 3) . x^{3} . y . y^{2} = - 6 x^{3} y^{3}$

Câu 12. Giá trị của đơn thức $5 x^{4} y^{2} z^{3}$ tại $x = - 1; y = - 1; z = - 2$ là

A. 10

B. 20

C. – 40

D. 40

Hiển thị đáp án

Đáp án đúng là: C

Thay $x = - 1; y = - 1; z = - 2$ vào đơn thức $5 x^{4} y^{2} z^{3}$ ta được:

$5 . {(- 1)}^{4} . {(- 1)}^{2} . {(- 2)}^{3} = - 40$

Câu 13. Tổng các đơn thức $3 x^{2} y^{4}$ và $7 x^{2} y^{4}$ là

A. $10 x^{2} y^{4}$

B. $9 x^{2} y^{4}$

C. $- 9 x^{2} y^{4}$

D. $- 4 x^{2} y^{4}$

Hiển thị đáp án

Đáp án đúng là: A

${3x}^{2} y^{4} + 7 x^{2} y^{4} = (3 + 7) x^{2} y^{4}$

Câu 14. Hiệu của hai đơn thức $- 9 y^{2} z$ và $- 12 y^{2} z$ là

A. $- 21 y^{2} z$

B. $- 3 y^{2} z$

C. $3 y^{4} z^{2}$

D. $3 y^{2} z$

Hiển thị đáp án

Đáp án đúng là: D

$- 9 y^{2} z - (- 12 y^{2} z) = (- 9 + 12) y^{2} z = 3 y^{2} z$

Câu 15. Thu gọn các đơn thức đồng dạng trong biểu thức $\frac{1}{2} {xy}^{2} - \frac{1}{3} y^{2} - (- \frac{2}{5} {xy}^{2}) + \frac{2}{5} y^{2}$ ta được

A. $\frac{9}{10} {xy}^{2} + \frac{1}{15} y^{2}$

B. $\frac{1}{15} {xy}^{2} + \frac{9}{10} y^{2}$

C. $\frac{9}{10} {xy}^{2} - \frac{1}{15} y^{2}$

D. $- \frac{9}{10} {xy}^{2} + \frac{1}{15} y^{2}$

Hiển thị đáp án

Đáp án đúng là: A

$\frac{1}{2} {xy}^{2} - \frac{1}{3} y^{2} - (- \frac{2}{5} {xy}^{2}) + \frac{2}{5} y^{2}$

$= \frac{1}{2} {xy}^{2} + \frac{2}{15} {xy}^{2} + \frac{2}{5} y^{2} - \frac{1}{3} y^{2}$

$= \frac{9}{10} {xy}^{2} + \frac{1}{15} y^{2}$

B. Lý thuyết

Sơ đồ tư duy Toán 8 Bài 1: Đơn thức

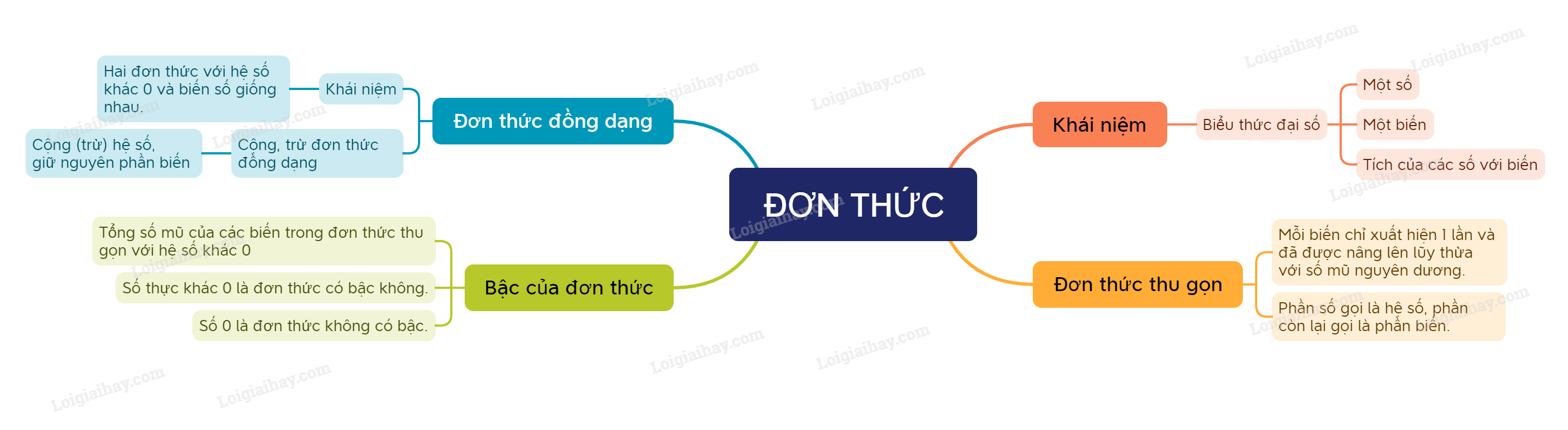
TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 1: Đơn thức - Ảnh 1

1. Đơn thức và đơn thức thu gọn

Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.

Số 0 được gọi là đơn thức không.

Ví dụ: $1; 2 x y; - \frac{3}{4} x^{2} y (- 4 x); . . .$ là các đơn thức.

Đơn thức thu gọn là đơn thức chỉ gồm một số, hoặc có dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.

Ví dụ:

$1; 2 x y; 5 x^{2} y^{4} z; . . .$ là các đơn thức thu gọn.

$3 x^{2} y x; - \frac{3}{4} x^{2} y (- 4 x); . . .$ không phải là các đơn thức thu gọn.

Với các đơn chưa là đơn thức thu gọn, ta có thể thu gọn chúng bằng cách áp dụng các tính chất của phép nhân và phép nâng lên lũy thừa.

Ví dụ: $- \frac{3}{4} x^{2} y (- 4 x) = (- \frac{3}{4}) . (- 4) . (x^{2} . x) . y = 3 x^{3} . y$

Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.

Chú ý: + Số thực khác 0 là đơn thức bậc không.

+ Số 0 được gọi là đơn thức không có bậc.

Ví dụ: $2 x y$ có bậc là $1 + 1 = 2$

$5 x^{2} y^{4} z$ có bậc là $2 + 4 + 1 = 7$

Với những đơn thức chưa thu gọn, ta nên thu gọn đơn thức trước, khi đó, bậc của đơn thức thu gọn chính là bậc của đơn thức ban đầu.

Ví dụ: $- \frac{3}{4} x^{2} y (- 4 x)$ có đơn thức thu gọn là $3 x^{3} . y$ , đơn thức này có bậc là $3 + 1 = 4$ nên đơn thức $- \frac{3}{4} x^{2} y (- 4 x)$ có bậc là 4.

Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.

Ví dụ: đơn thức $3 x^{3} . y$ có hệ số là 3, phần biến là $x^{3} . y$ .

2. Đơn thức đồng dạng

Hai đơn thức đồng dạng là hai đơn thức với hệ số khác 0 và có phần biến giống nhau.

- Cộng và trừ đơn thức đồng dạng: muốn cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.

Xem thêm các bài trắc nghiệm Toán 8 Kết nối tri thức hay, có đáp án khác:

Trắc nghiệm Bài 2: Đa thức

Trắc nghiệm Bài 3: Phép cộng và phép trừ đa thức

Trắc nghiệm Bài 4: Phép nhân đa thức

Trắc nghiệm Bài 5: Phép chia đa thức cho đơn thức

Trắc nghiệm Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Được cập nhật 10/03/2024 169 lượt xem

Bởi Hà Linh

Chủ đề: Trắc nghiệm toán 8 Đơn thức

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Trắc nghiệm Toán 8 - KNTT

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

1900.edu.vn xin giới thiệu Bộ trắc nghiệm Toán 8 Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ sách Kết nối tri thức hay, có đáp án sẽ giúp học sinh dễ dàng ôn tập kiến thức Toán 8 Bài 20. Mời các bạn đón xem:

155 1 năm trước

Trắc nghiệm Toán 8 - KNTT

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

1900.edu.vn xin giới thiệu Bộ trắc nghiệm Toán 8 Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ sách Kết nối tri thức hay, có đáp án sẽ giúp học sinh dễ dàng ôn tập kiến thức Toán 8 Bài 19. Mời các bạn đón xem:

128 1 năm trước

Trắc nghiệm Toán 8 - KNTT

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 18: Thu thập và phân loại dữ liệu

1900.edu.vn xin giới thiệu Bộ trắc nghiệm Toán 8 Bài 18: Thu thập và phân loại dữ liệu sách Kết nối tri thức hay, có đáp án sẽ giúp học sinh dễ dàng ôn tập kiến thức Toán 8 Bài 18. Mời các bạn đón xem:

89 1 năm trước

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 1: Đơn thức

1900.edu.vn xin giới thiệu Bộ trắc nghiệm Toán 8 Bài 1: Đơn thức sách Kết nối tri thức hay, có đáp án sẽ giúp học sinh dễ dàng ôn tập kiến thức Toán 8 Bài 1. Mời các bạn đón xem:

A. Trắc nghiệm

B. Lý thuyết

Bình luận (0)

Bài viết cùng chủ đề

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

TOP 15 câu Trắc nghiệm Toán 8 (Kết nối tri thức) Bài 18: Thu thập và phân loại dữ liệu

Nội dung bài viết