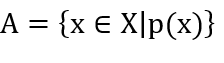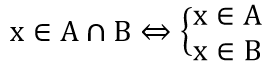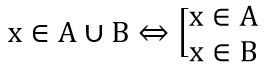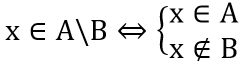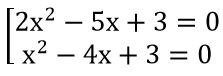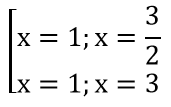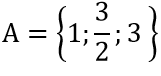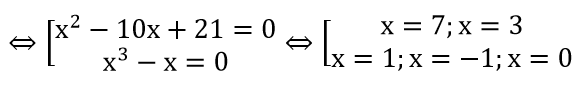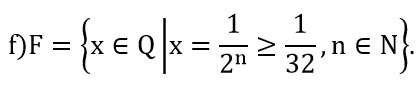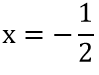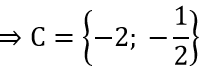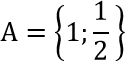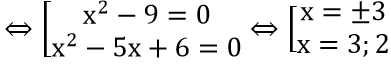Tập hợp và các phép toán trên tập hợp
Lý thuyết
1. Tập hợp - Phần tử
+ Tập hợp, phần tử là những khái niệm cơ bản của toán học.
Các đối tượng có chung một hay nhiều tính chất quy tụ lại thành một tập hợp; mỗi đối tượng là một phần tử.
+ Mỗi tập hợp được xác định bởi:
- Liệt kê các phần tử của nó: A={a1; a2; a3;…}
- Chỉ ra các tính chất đặc trưng cho các phần tử của nó:
2. Tập hợp rỗng
Tập hợp rỗng, kí hiệu là ∅ , là tập hợp không chứa phần tử nào.
A ≠ ∅ ⇔ ∃x : x ∈ A
3. Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B, kí hiệu là A ⊂ B.
A ⊂ B ⇔ ∀x : x ∈ A ⇒ x ∈ B.
A ⊄ B ⇔ ∀x : x ∈ A ⇒ x ∉ B.
Tính chất:
1) A ⊂ A với mọi tập A.
2) Nếu A ⊂ B và B ⊂ C thì A ⊂ C.
3) ∅ ⊂ A với mọi tập hợp A.
4.Tập hợp bằng nhau.
Khi A ⊂ B và B ⊂ A thì ta nói tập hợp A bằng tập hợp B và viết là A = B.
A = B ⇔(∀x : x ∈ A ⇔ x ∈ B )
5. Giao của hai tập hợp
Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.
6. Hợp của hai tập hợp
Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B.
7. Hiệu và phần bù của hai tập hợp
Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B.
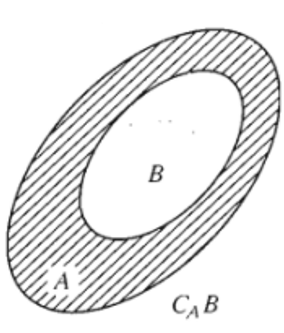
Khi B ⊂ A thì tất các phần tử thuộc A mà không là phần tử của B (A\B) gọi là phần bù của B trong A, kí hiệu CA B (phần gạch chéo trong hình).
8. Các tập hợp con thường dùng của R
Khoảng:
(a;b)={x ∈ R|a < x < b}
(a;+∞)={x ∈ R|a < x}
(-∞;b)={x ∈ R|x < b}
Đoạn:
[a;b]={x ∈ R|a ≤ x ≤ b}
Nửa khoảng:
[a;b)={x ∈ R |a ≤ x < b}
(a;b]={x ∈ R |a < x ≤ b}
[a;+∞)={ x ∈ R | a ≤ x}
(-∞;b]={ x ∈ R | x ≤ b}
Bài tập vận dụng (có đáp án)
Bài 1: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó
a) A={x ∈ R|(2x2 - 5x + 3)(x2 - 4x + 3)= 0}.
b) B={x ∈ R|(x2 - 10x + 21)(x3 - x)= 0}.
c) C={x ∈ N|x + 3 < 4 + 2x; 5x - 3 < 4x - 1}.
d) D={x ∈ Z||x + 2| ≤ 3}.
e) E={x ∈ R|x2 + x + 3 = 0}.
Bài 2: Viết các tập sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:
a) A = {0; 1; 2; 3; 4}
b) B ={ -3; 9; -27; 81}
e) E = Tập tất cả các điểm thuộc đường trung trực của đoạn thẳng AB.
f) F = Tập tất cả các điểm thuộc đường tròn tâm I cho trước và có bán kính bằng 5.
Bài 3: Cho biết mỗi tập hợp sau có bao nhiêu tập hợp con, tìm tất cả các tập hợp con của tập hợp sau:
a) A = {1; 2}
b) B = {1; 2; 3}
c) C={x ∈ R|2x2-5x+2=0}
d) D={x ∈ Q|x2-4x+2=0}
Bài 4: Trong các tập hợp sau, tập nào là tập con của tập nào?
a)
| A = {1; 2; 3}, | B ={x ∈ N|x < 4}, |
| C ={0; +∞}, | D ={x ∈ R|2x2 - 7x + 3 = 0} |
b)
| A = Tập các ước số tự nhiên của 6; | B = Tập các ước số tự nhiên của 12; |
c)
| A = Tập các hình bình hành; | B = Tập các hình chữ nhật; |
| C = Tập các hình thoi; | D = Tập các hình vuông, |
d)
| A = Tập các tam giác cân; | B = Tập các tam giác đều; |
| C = Tập các tam giác vuông; | D = Tập các tam giác vuông cân. |
Bài 5: Tìm A ∩ B;A ∪ B;A\B;B\A với
a) A={2,4,7,8,9,12};B={2,8,9,12}.
b) A={x ∈ Q|2x2 - 3x + 1 = 0};B={x ∈ R||2x - 1|= 1}
c) A = Tập các ước số của 12; B = Tập hợp các ước số của 18.
d) A={x ∈ N|(x2 - 9)(x2 - 5x + 6 = 0}; B = Tập các số nguyên tố có 1 chữ số.
Bài 6: Xác định các tập hợp A, B sao cho:
A ∩ B ={0,1,2,3,4}; A \ B ={-3,-2};B \ A ={6,9,10}.
Bài 7: Mỗi học sinh lớp 10A đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn thể thao này. Hỏi lớp 10A có bao nhiêu học sinh?
Bài 8: Kết quả điều tra ở một lớp cho thấy: có 20 hoc sinh thích bóng đá, 17 học sinh thích bơi, 36 học sinh thích chơi bóng chuyền, 14 học sinh thích bóng đá và bơi, 13 học sinh thích bơi và bóng chuyền, 15 học sinh thích bóng đá và bóng chuyền, 10 học sinh thích cả ba môn, 12 học sinh không thich môn nào. Tính xem lơp học có bao nhiêu học sinh?
Bài 9: Trong 100 học sinh lớp 10, có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được cả hai tiếng Anh và Pháp.
Bài 10: Cho các tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 2, 3, 4};
C = {2, 4, 6, 8}. Hãy xác định: CA B; CA C;CA (B ∪ C).
Đáp án và hướng dẫn giải
Bài 1: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó
a) (2x2-5x+3)(x2-4x+3)=0⇔
⇔
⇒
b) (x2 - 10x + 21)(x3 - x)=0
⇒ B={-1;0;1;3;7 }.
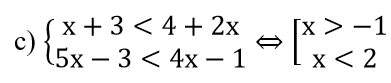
⇒ C={0;1}
d) D={x ∈ Z||x + 2| ≤ 3}.
|x + 2| ≤ 3 ⇔ -3 < x + 2 < 3 ⇔ - 5 < x < 1
⇒ D={-4; -3; -2; -1;0}
e)E={x ∈ R|x2 + x + 3 = 0}.
x2 + x + 3 = 0: Phương trình này vô nghiệm do đó E = ∅
Bài 2: Viết các tập sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:
a) A = {0; 1; 2; 3; 4}
A={x ∈ N|x ≤ 4}
b) B ={ -3; 9; -27; 81}
B={x ∈ Z|x=(-3)n ;n < 5;n ∈ N}
e) E = Tập tất cả các điểm thuộc đường trung trực của đoạn thẳng AB.
E = Tập tất cả các điểm cách đều hai đầu mút A và B
Hay E = Tập tất cả các điểm I sao cho IA = IB.
f) F = Tập tất cả các điểm thuộc đường tròn tâm I cho trước và có bán kính bằng 5.
F = Tập tất cả các điểm cách điểm I một khoảng bằng 5.
Bài 3: Cho biết mỗi tập hợp sau có bao nhiêu tập hợp con, tìm tất cả các tập hợp con của tập hợp sau:
a) A = {1; 2}
A có 2 phần tử nên A có 22 = 4 tập con
Các tập hợp con của A là: {1;2}; {1}; {2}; ∅ .
b) B = {1; 2; 3}
B có 3 phần tử nên A có 23 = 8 tập con
Các tập hợp con của B là: {1; 2; 3} {1;2};{1;3}; {2;3}; {1}; {2};{3}; ∅ .
c) C={x ∈ R|2x2 - 5x + 2 = 0}
2x2 - 5x + 2 = 0 ⇔ x = -2;
C có 2 phần tử nên C có 22 = 4 tập con
Các tập hợp con của C là: 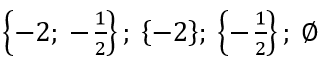
d) D={x ∈ Q|x2 - 4x + 2 = 0}
x2 - 4x + 2 = 0 ⇔ x = 2 ± √2
Do x ∈ Q nên D = ∅ .
Do đó, D có 1 tập con là chính nó.
Bài 4:
| a) A = {1; 2; 3}, | B={x ∈ N|x < 4}, |
| C={0; +∞}, | D={x ∈ R|2x2 - 7x + 3 = 0} |
Ta có: B={x ∈ N|x < 4} ⇒ B={0;1 ;2;3}
D={x ∈ R|2x2 - 7x + 3 = 0} ⇒ 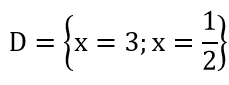
Khi đó: A ⊂ B ⊂ C và D ⊂ C.
b) A = Tập các ước số tự nhiên của 6 ⇒ A={1;2;3;6}
B = Tập các ước số tự nhiên của 12 ⇒ B={1;2;3;4;6;12}
Khi đó A ⊂ B
c)
| A = Tập các hình bình hành; | B = Tập các hình chữ nhật; |
| C = Tập các hình thoi; | D = Tập các hình vuông, |
Ta có: D ⊂ B ⊂ A và D ⊂ C
d)
| A = Tập các tam giác cân; | B = Tập các tam giác đều; |
| C = Tập các tam giác vuông; | D = Tập các tam giác vuông cân. |
Ta có: B ⊂ A; D ⊂ C, D ⊂ A.
Bài 5: Tìm A ∩ B;A ∪ B;A \ B;B \ A với
a) A={2,4,7,8,9,12};B={2,8,9,12}.
A ∩ B={2;8;9;12}; A ∪ B={2,4,7,8,9,12};
A\B={4;7}; B \ A = ∅ .
b) A={x ∈ Q|2x2 - 3x + 1 = 0};B={x ∈ R||2x - 1|= 1}
2x2 - 3x + 1 = 0⇔x=1;x=1/2 ⇒
|2x - 1|= 1 ⇔ x = 0; x = 1 ⇒ B ={0;1 }
A ∩ B = {1};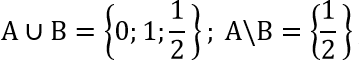
c) A = Tập các ước số của 12 ⇒ A={1;2;3;4;6;12}
B = Tập hợp các ước số của 18 ⇒ B={1;2;3;6;9;18}
A ∩ B={1;2;3;6}; A ∪ B={1;2;3;4;6;9;12;18}
A \ B={4;12}; B \ A={9;18}
d) A={x ∈ N|(x2 - 9)(x2 - 5x + 6 = 0};
(x2 - 9)(x2 - 5x + 6)= 0
⇒ A={-3;2;3}
B = Tập các số nguyên tố có 1 chữ số.
B={2;3;5;7}
A ∩ B={2;3}; A ∪ B={-3;2;3;5;7}; A \ B={-3};B \ A={5;7}.
Bài 6:
a) A ∩ B={0,1,2,3,4}; A\B={-3,-2};B\A={6,9,10}.
A ∩ B={0,1,2,3,4} ⇒ 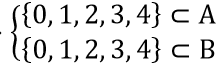
A\B={-3,-2} ⇒ 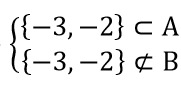
B\A={6,9,10} ⇒ 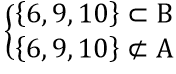
⇒ A={0,1,2,3,4} ∪ {-3,-2}={-3,-2,0,1,2,3,4 }
B={0,1,2,3,4} ∪ {6,9,10}={0,1,2,3,4,6,9,10}
Bài 7:
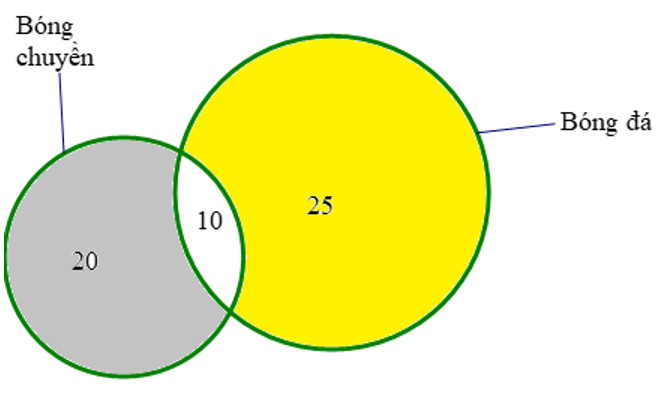
Từ sơ đồ ta thấy: Số học sing của lớp 10A là: 25 + 20 – 10 = 35 (học sinh)
Bài 8:
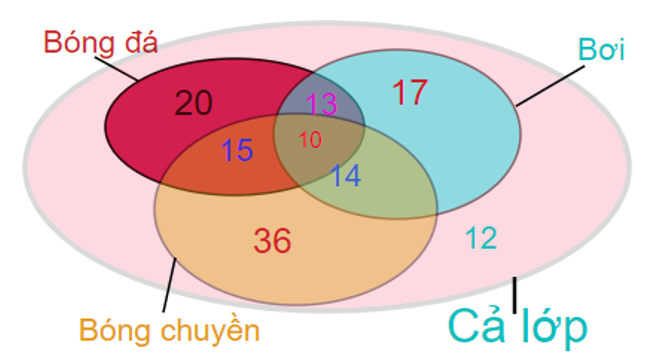
Từ sơ đồ trên, ta có:
Số học sinh của cả lớp là:
20 + 17 + 36 - (13 + 14 + 15) + 10 = 53 (học sinh)
Bài 9:
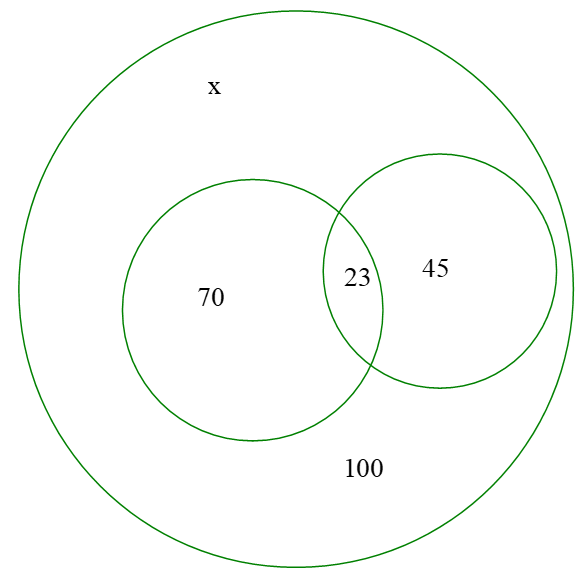
Gọi số học sinh không nói được cả Tiếng Anh và tiếng Pháp là x
x + 70 + 45 - 23 = 100 ⇒ x=8 học sinh.
Bài 10: A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 2, 3, 4};
C = {2, 4, 6, 8}.
CA B={5,6,7,8,9}; CA C={1,3,5,7,9}
B ∪ C={1, 2, 3, 4, 6, 8} ⇒ CA (B ∪ C)={5;7;9}
Xem thêm các dạng bài tập liên quan khác:
100 Bài tập Mệnh đề (có đáp án)
Mệnh đề kéo theo và ví dụ mới nhất 2024
500 Bài tập Toán 10 Mệnh đề và tập hợp (có đáp án năm 2024)
80 Bài tập về Tập hợp và các phép toán trên tập hợp (có đáp án năm 2024)