100 Bài tập Mệnh đề (có đáp án) - Toán 10

Bài giảng Toán 10 Bài 1: Mệnh đề - Kết nối tri thức

Lý thuyết

1. Mệnh đề, mệnh đề chứa biến

1.1. Mệnh đề

- Những khẳng định có tính đúng hoặc sai gọi là mệnh đề logic (gọi tắt là mệnh đề). Những câu không xác định được tính đúng sai không phải là mệnh đề.

- Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai.

Ví dụ 1:

Câu “Hoa hồng rất đẹp nhất trong các loài hoa” là câu khẳng định nhưng không xác định được tính đúng sai nên câu này không là mệnh đề.

Câu “Bây giờ là mấy giờ?” là một câu hỏi không xác định được tính đúng sai nên câu này không là mệnh đề.

Câu “8 + 1 > 9” là một câu khẳng định có thể xác định được tính đúng sai nên câu này là mệnh đề.

Câu “Số 1 tỉ là số rất lớn” là một câu khẳng định tuy nhiên câu này mang tính quan điểm cá nhân không xác định đước tính đúng sai nên không là mệnh đề.

Chú ý:

- Người ta thường sử dụng các chữ cái P, Q, R, … để biểu thị các mệnh đề.

- Những mệnh đề liên quan đến toán học được gọi là mệnh đề toán học.

- Những câu nghi vấn, câu cảm thán, câu cầu khiến không phải là mệnh đề.

Ví dụ 2:

+ “Hà Nội là thủ đô của Việt Nam” là một mệnh đề nhưng không phải mệnh đề toán học vì không phải sự kiện trong toán học.

+ “Số π là một số hữu tỉ” là mệnh đề toán học.

1.2. Mệnh đề chứa biến

- Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập D nào đó mà với mỗi giá trị của biến thuộc vào D ta được một mệnh đề.

- Ta thường kí hiệu mệnh đề chứa biến n là P(n); mệnh đề chứa biến x, y là P(x, y), ….

Ví dụ:

+ “Với mọi giá trị thực của biến x, |x| ≥ x”: không phải là mệnh đề chứa biến vì:

Ta có |x| ≥ x với mọi giá trị thực của biến x nên đây là khẳng định đúng. Do đó phát biểu này là một mệnh đề không phải mệnh đề chứa biến.

+ “5n chia hết cho 2” là mệnh đề chứa biến.

Khi n = 4 thì mệnh đề này là mệnh đề đúng, khi n = 5 thì mệnh đề này là mệnh đề sai.

2. Mệnh đề phủ định

- Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Ta kí hiệu mệnh đề phủ định của mệnh đề P là $\overline{P}$.

- Mệnh đề P và mệnh đề $\overline{P}$ là hai phát biểu trái ngược nhau. Nếu P đúng thì $\overline{P}$ sai, còn nếu P sai thì $\overline{P}$ đúng.

Ví dụ: “5 không chia hết cho 3” là mệnh đề phủ định của mệnh đề “5 chia hết cho 3”;

“3 là hợp số” là mệnh đề phủ định của mệnh đề “3 không là hợp số”.

3. Mệnh đề kéo theo, mệnh đề đảo

3.1. Mệnh đề kéo theo

- Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo và kí hiệu là P ⇒ Q.

- Các định lí toán học là những mệnh đề đúng và thường có dạng P ⇒ Q. Khi đó ta nói:

P là giả thiết của định lí, Q là kết luận của định lí hoặc

“P là điều kiện đủ để có Q”, hoặc “Q là điều kiện cần để có P”.

Chú ý: Mệnh đề P ⇒ Q chỉ sai khi P đúng và Q sai. Do đó ta chỉ cần xét tính đúng sai của mệnh đề P ⇒ Q khi P đúng. Khi đó, nếu Q đúng thì P ⇒ Q đúng, nếu Q sai thì P ⇒ Q sai.

Ví dụ: Cho 2 mệnh đề: P: “9 chia hết cho 9”; Q: “9 chia hết cho 3”.

“Nếu 9 chia hết cho 9 thì 9 chia hết cho 3” là mệnh đề kéo theo của P và Q.

P là mệnh đề đúng và Q là mệnh đề đúng nên mệnh đề kéo theo P ⇒ Q là mệnh đề đúng.

3.2. Mệnh đề đảo

- Mệnh đề Q ⇒ P được gọi là mệnh đề đảo của mệnh đề P ⇒ Q.

Nhận xét: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.

Ví dụ: Cho 2 mệnh đề: P: “n = 0”; Q: “n là số nguyên”.

Mệnh đề kéo theo P ⇒ Q được phát biểu là: “Nếu n = 0 thì n là số nguyên”.

Mệnh đề đảo Q ⇒ P được phát biểu là “Nếu n là số nguyên thì n = 0”.

- Mệnh đề P ⇒ Q là mệnh đề đúng còn mệnh đề Q ⇒ P không đúng.

4. Mệnh đề tương đương

- Mệnh đề “P nếu và chỉ nếu Q” được gọi là một mệnh đề tương đương và kí hiệu P ⇔ Q .

Nhận xét:

- Nếu cả hai mệnh đề Q ⇒ P và P ⇒ Q đều đúng thì hai mệnh đề tương đương P ⇔ Q đúng. Khi đó ta nói “P tương đương với Q” hoặc “P là điều kiện cần và đủ để có Q” hoặc “P khi và chỉ khi Q”.

Ví dụ: Cho 2 mệnh đề: P: “Tứ giác ABCD là hình bình hành”; Q: “Tứ giác ABCD có hai cặp cạnh đối song song”.

“Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai cặp cạnh đối song song” là mệnh đề P ⇒ Q.

“Nếu tứ giác ABCD có hai cặp cạnh đối song song thì tứ giác ABCD là hình bình hành” là mệnh đề Q ⇒ P.

Hai mệnh đề này đều đúng nên P và Q là hai mệnh đề tương đương.

Khi đó mệnh đề P ⇔ Q được phát biểu như sau: “Tứ giác ABCD là hình bình hành khi và chỉ khi tứ giác ABCD có hai cặp cạnh đối song song”.

5. Mệnh đề có chứa kí hiệu ∀ và ∃

- Kí hiệu ∀ đọc là “với mọi”.

- Kí hiệu ∃ đọc là “có một” hoặc “tồn tại”.

- Cho mệnh đề “$P\left(x\right),x\in D$”.

+ Phủ định của mệnh đề “$\forall x\in D,P\left(x\right)$” là mệnh đề “$\exists x\in D,\overline{P\left(x\right)}$”.

+ Phủ định của mệnh đề “$\exists x\in D,P\left(x\right)$” là mệnh đề “$\forall x\in D,\overline{P\left(x\right)}$”.

Chú ý: 

+ Phát biểu “Với mọi số tự nhiên n” có thể kí hiệu là $\forall n\in \mathbb{N}$.

+ Phát biểu “Tồn tại số tự nhiên n” có thể kí hiệu là $\exists n\in \mathbb{N}$.

Ví dụ:

Phủ định của mệnh đề “$\exists x\in ℝ,x^2+1=0$” là mệnh đề: “$\forall x\in ℝ,x^2+1\ne 0$”.

Các dạng bài tập toán về mệnh đề và phương pháp giải

Dạng 1: Xác định mệnh đề và mệnh đề chứa biến

1. Phương pháp giải

- Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:

+ Mệnh đề là một câu khẳng định đúng hoặc sai.

Một mệnh đề không thể vừa đúng vừa sai

+ Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập X nào đó mà với mỗi giá trị chứa biến thuộc X ta được một mệnh đề.

2. Bài tập tự luyện

2.1. Bài tập tự luận

Bài 1. Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai.

(1) Ở đây đẹp quá!

(2) Phương trình x² - 3x + 1 = 0 vô nghiệm.

(3) 16 không là số nguyên tố.

(4) Hai phương trình x² - 4x + 3 = 0 và x² - $\sqrt{x+3}$ + 1 = 0 có nghiệm chung.

(5) Số $\pi$ có lớn hơn 3 hay không?

(6) Italia vô địch Worldcup 2006.

(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.

(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.

Hướng dẫn giải

Câu (1) và (5) không là mệnh đề (vì là câu cảm thán, câu hỏi).

Các câu (3), (4), (6), (8) là những mệnh đề đúng.

Câu (2) và (7) là những mệnh đề sai.

Bài 2. Cho ba mệnh đề sau, với n là số tự nhiên

(1) n + 8 là số chính phương.

(2) Chữ số tận cùng của n là 4

(3) n - 1 là số chính phương.

Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng mệnh đề nào sai?

Hướng dẫn giải

Ta có số chính phương có các chữ số tận cùng là 0, 1, 4, 5, 6, 9. Vì vậy:

+ Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là đúng thì n + 8 có chữ số tận cùng là 2 nên không thể là số chính phương. Vậy trong hai mệnh đề này phải có một mệnh đề là đúng và một mệnh đề là sai.

+ Tương tự, nhận thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì n - 1 có chữ số tận cùng là 3 nên không thể là số chính phương.

Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.

Bài 3. Trong các câu sau, có bao nhiêu câu là mệnh đề, mệnh đề chứa biến, không là mệnh đề?

- Hãy cố gắng học thật tốt !

- Số B = $(-\infty ; 3)$ chia hết cho $A\cap B=[-1;3).$

- Số A = $[1;+\infty )$ là số nguyên tố.

- Số B = {x$\in \mathrm{ℝ}|x^2+1=0$} là số chẵn.

Hướng dẫn giải

Có hai mệnh đề là:

- Số B = $(-\infty ; 3)$ chia hết cho $A\cap B=[-1;3).$

- Số A = $[1;+\infty )$ là số nguyên tố.

Có một mệnh đề chứa biến là: 

- Số B = {x$\in \mathrm{ℝ}|x^2+1=0$} là số chẵn.

Có một câu không là mệnh đề là:

- Hãy cố gắng học thật tốt !

Bài 4. Trong các phát biểu sau, phát biểu nào không phải là mệnh đề, giải thích?

a) Không được vào đây!

b) Ngày mai bạn đi học không?

c) Chủ tịch Hồ Chí Minh sinh năm 1890.

d) 17 chia 3 dư 1.

e) 2003 không là số nguyên tố.

f) x² - 3x + 2 = 0

Hướng dẫn giải

a) Câu a) không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.

b) Câu b) không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

c) Câu c) là mệnh đề vì đó là câu khẳng định tính đúng sai.

d) Câu d) là mệnh đề vì đó là câu khẳng định tính đúng sai.

e) Câu e) là mệnh đề vì đó là câu khẳng định tính đúng sai.

f) Câu f) không phải là mệnh đề vì nó là mệnh đề chứa biến

Vậy có 3 câu không phải mệnh đề

Bài 5. Tìm tất cả các giá trị thực của x để mệnh đề P:"|2x-1|$\ge$1" là mệnh đề đúng?

Hướng dẫn giải

Ta có |2x-1|$\ge$1 $\left[\begin{array}{l}2x-1\ge 1\\ 2x-1\le -1\end{array}\right.\iff \left[\begin{array}{l}x\ge 1\\ x\le 0\end{array}\right.$

Bài 6. Tìm tất cả các giá trị thực của x để mệnh đề P:"2x-1$\ge$0" là mệnh đề sai?

Hướng dẫn giải

Mệnh đề P:" 2x - 1$\ge$0" sai khi và chỉ khi 2x - 1< 0 đúng $\iff x<\frac{1}{2}$

Bài 7. Xét câu: P(n): "n là số tự nhiên nhỏ hơn 50 và n chia hết cho 12". Với giá trị nào của n sau đây thì P(n) là mệnh đề đúng. Khi đó các giá trị của n bằng bao nhiêu?

Hướng dẫn giải

Các số thỏa mãn yêu cầu bài toán là 0; 12; 24; 36; 48.

2.2. Bài tập trắc nghiệm

Bài 1. Cho các câu sau đây:

a) Không được vào đây!

b) Ngày mai bạn đi học không?

c) Chủ tịch Hồ Chí Minh sinh năm 1890.

d) 17 chia 3 dư 1.

e) 2003 không là số nguyên tố.

Có bao nhiêu câu là mệnh đề ?

A. 2;

B. 1;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: C.

a) Câu a) không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.

b) Câu b) không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

c) Câu c) là mệnh đề vì đó là câu khẳng định tính đúng sai.

d) Câu d) là mệnh đề vì đó là câu khẳng định tính đúng sai.

e) Câu e) là mệnh đề vì đó là câu khẳng định tính đúng sai.

Vậy có 3 câu là mệnh đề.

Bài 2. Câu nào dưới dây không phải là mệnh đề?

A. 78 + 12 – 8 = 89;

B. 18 có chia hết cho 2 không?;

C. Ngày mai là chủ nhật;

D. Phương trình x² + 2x – 2 = 0 có hai nghiệm phân biệt.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Đây là mệnh đề vì nó khẳng định tính đúng sai.

B. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

C. Đây là mệnh đề vì nó khẳng định tính đúng sai.

D. Đây là mệnh đề vì nó khẳng định tính đúng sai.

Bài 3. Xét các câu sau, câu nào là mệnh đề chứa biến?

A. Bạn có rảnh tối nay không?;

B. x + 2 = 11;

C. 5 + 9 = 14;

D. Huế là một thành phố của Việt Nam.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Câu trên là câu hỏi nên nó không phải là mệnh đề chứa biến.

B. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến và ta có tập D của các biến x để câu trên đúng hoặc sai.

C. Câu trên là mệnh đề vì đó là câu khẳng định tính đúng sai.

Nên câu trên không phải là mệnh đề chứa biến.

D. Câu trên là mệnh đề vì đó là câu khẳng định tính đúng sai.

Nên câu trên không phải là mệnh đề chứa biến.

Bài 4. Trong các câu sau đây, câu nào là mệnh đề toán học?

A. Dừng lại!;

B. Hà Nội là thủ đô của Việt Nam;

C. Dân tộc Kinh là dân tộc đông dân nhất;

D. 41 + 7 + 4 = 55.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Câu A không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.

B. Câu B là mệnh đề vì đó là câu khẳng định tính đúng sai.

Tuy nhiên câu trên không phải là mệnh đề toán học vì nó không liên quan đến toán học.

C. Câu C là mệnh đề vì đó là câu khẳng định tính đúng sai.

Tuy nhiên câu trên không phải là mệnh đề toán học vì nó không liên quan đến toán học.

D. Câu D là mệnh đề vì đó là câu khẳng định tính đúng sai.

Vì mệnh đề trên liên quan đến toán học nên đó là mệnh đề toán học.

Bài 5. Trong các câu dưới đây, câu nào không phải là mệnh đề?

A. Phương trình  x² + x + 1 = 0 vô nghiệm;

B. 39 chia hết cho 3 và cho 13;

C. 5 + 4 = 10;

D. x – 2y và 2xy.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Câu A là mệnh đề vì đó là câu khẳng định tính đúng sai.

B. Câu B là mệnh đề vì đó là câu khẳng định tính đúng sai.

C. Câu C là mệnh đề vì đó là câu khẳng định tính đúng sai.

D. Câu D không phải là mệnh đề vì nó phụ thuộc biến và không khẳng định tính đúng sai.

Bài 6. Trong các câu dưới đây, câu nào là mệnh đề?

A. Có ai ở trong đó không?;

B. Bạn có thấy đói không?;

C. Đừng lại gần tôi!;

D. Số 25 không phải là số nguyên tố.

Hướng dẫn giải :

Đáp án đúng là: D.

A. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

B. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

C. Câu trên không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.

D. Câu này là mệnh đề vì nó khẳng định tính đúng sai.

Bài 7. Trong các câu sau, có bao nhiêu câu là mệnh đề?

(1) Đi ngủ sớm đi!

(2) Số 22 chia hết cho 2 và 4.

(3) Bạn học trường nào?

(4) x là số nguyên tố.

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: A.

Xét từng mệnh đề ta có:

+ Câu (1) không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.

+ Câu (2) là mệnh đề vì đó là câu khẳng định tính đúng sai.

+ Câu (3) không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

+ Câu (4) không phải là mệnh đề vì nó phụ thuộc vào biến và chưa khẳng định tính đúng sai.

Vậy có 1 câu là mệnh đề.

Bài 8. Câu nào sau đây không phải là mệnh đề chứa biến?

A. x² + x + 1 > 0;

B. 4 < 5;

C. x là số tự nhiên;

D. x + 6 = 12.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến và ta có tập D của các biến x để câu trên đúng hoặc sai.

B. Câu B là mệnh đề vì đó là câu khẳng định tính đúng sai.

Nên câu trên không phải là mệnh đề chứa biến.

C. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến và ta có tập D của các biến x để câu trên đúng hoặc sai.

D. Câu trên là mệnh đề chứa biến vì câu trên phụ thuộc vào biến và ta có tập D của các biến x để câu trên đúng hoặc sai.

Bài 9. Câu nào sau đây là mệnh đề?

A. Mệnh đề là gì?;

B. Số 30 là số tự nhiên có hai chữ số;

C. Không được làm ồn!;

D. 3x + 2 < 5.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

B. Câu trên là mệnh đề vì nó khẳng định tính đúng sai.

C. Câu trên không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.

D. Câu trên không phải là mệnh đề vì nó còn phụ thuộc vào biến và chưa khẳng định được tính đúng sai.

Bài 10. Câu nào sau đây không phải là mệnh đề toán học?

A. Phương trình x² + 6x – 2 = 0 có hai nghiệm dương phân biệt;

B. Số 24 chia hết cho 4 và 6;

C. Số 6 là số chính phương;

D. Lớp 11A có 45 học sinh.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Câu A là mệnh đề vì đó là câu khẳng định tính đúng sai.

Vì mệnh đề trên liên quan đến toán học nên đó là mệnh đề toán học.

B. Câu B là mệnh đề vì đó là câu khẳng định tính đúng sai.

Vì mệnh đề trên liên quan đến toán học nên đó là mệnh đề toán học.

C. Câu C là mệnh đề vì đó là câu khẳng định tính đúng sai.

Vì mệnh đề trên liên quan đến toán học nên đó là mệnh đề toán học.

D. Câu D là mệnh đề vì đó là câu khẳng định tính đúng sai.

Tuy nhiên câu trên không phải là mệnh đề toán học vì nó không liên quan đến toán học.

Dạng 2: Xét tính đúng sai của một mệnh đề

1. Phương pháp giải

– Dựa vào định nghĩa mệnh đề để xác định tính đúng, sai của mệnh đề đó.

+ Nếu định nghĩa của mệnh đề đó đúng hay mệnh đề đó là một khẳng định đúng thì ta gọi đó là mệnh đề đúng.

+ Ngược lại, nếu định nghĩa của mệnh đề đó sai hay mệnh đề đó là một khẳng định sai thì ta gọi đó là mệnh đề sai.

Lưu ý: Một mệnh đề không thể vừa đúng và sai.

– Với mệnh đề chứa biến: Tìm tập D của các biến x để P(x) đúng hoặc sai.

2. Bài tập tự luyện

2.1. Bài tập tự luận

Bài 1. Xét tính đúng, sai của mệnh đề sau:

M: “π là một số hữu tỉ”.

N: “Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ ba”.

Hướng dẫn giải

- Mệnh đề M là một mệnh đề sai vì $\mathrm{\pi }$ là một số vô tỉ.

- Mệnh đề N đúng.

Bài 2. Xét tính đúng, sai của mệnh đề sau:

A: “Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn”.

B: “Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn”.

C: “Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”.

D: “Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”.

Hướng dẫn giải

- A là mệnh đề sai. Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1, 3 là số lẻ.

- B là mệnh đề sai. Ví dụ: 2.3 = 6 là số chẵn nhưng 3 là số lẻ.

- C là mệnh đề sai. Ví dụ 1 + 3 = 4 là số chẵn nhưng 1, 3 là số lẻ.

- D là mệnh đề đúng.

Bài 3. Xét tính đúng, sai của mệnh đề sau:

P: "$-\mathrm{\pi }<-2\iff {\mathrm{\pi }}^2<4.$".

Q: " $\mathrm{\pi }<4\iff {\mathrm{\pi }}^2<16.$".

Hướng dẫn giải

Ta có: ${\mathrm{\pi }}^2<4\iff \left|\mathrm{\pi }\right|<2\iff -2<\mathrm{\pi }<2.$ Suy ra P sai.

$\mathrm{\pi }<4\Rightarrow {\mathrm{\pi }}^2<16$. Suy ra Q đúng.

Bài 4. Xét tính đúng, sai của mệnh đề sau:

X: "$\sqrt{23}<5\iff 2\sqrt{23}<10$".

Y: "$\sqrt{23}<5\Rightarrow -2\sqrt{23}>-10$".

Hướng dẫn giải

Ta có: $\sqrt{23}<5\iff 2\sqrt{23}<2.5$. Suy ra X đúng.

$\sqrt{23}<5\Rightarrow -2\sqrt{23}>-2.5$. Suy ra Y đúng.

Bài 5. Xét tính đúng, sai của mệnh đề sau:

M: “Số nguyên tố lớn hơn 2 là số lẻ”.

N: “Số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5”.

P: “Bình phương tất cả các số nguyên đều chia hết cho 2”.

Hướng dẫn giải

- M là mệnh đề đúng. Vì mọi số lớn hơn 2 mà chữn thì đều chia hết cho 2, nên không thể là số nguyên tố.

- N là mệnh đề đúng.

- P là mệnh đề sai. Ví dụ: 3² = 9 nhưng 9 không chia hết cho 2.

Bài 6. Nêu mệnh đề phủ định của mỗi mệnh đề sau và xác định xem mệnh đề phủ định đó đúng hay sai:

a) P: “ Phương trình x² + x + 1 = 0 có nghiệm”.

b) Q: “ Năm 2020 là năm nhuận”.

c) R: “ 327 chia hết cho 3”.

Hướng dẫn giải

$\overline{P}$: “Phương trình $x^2+x+1=0$ vô nghiệm”. $\overline{P}$ là mệnh đề đúng.

$\overline{Q}$  : “Năm 2000 không phải là năm nhuận”. $\overline{Q}$  là mệnh đề sai.

$\overline{R}$  : “Số 327 không chia hết cho 3”. $\overline{R}$  là mệnh đề sai.

Bài 7. Cho tam giác ABC với đường trung tuyến AM. Xét hai mệnh đề

P: “Tam giác ABC vuông tại A”;

Q: “Trung tuyến AM bằng nửa cạnh BC ”

a) Phát biểu mệnh đề P $\Rightarrow$Q và cho biết mệnh đề này đúng hay sai.

b) Phát biểu mệnh đề P $\iff$Q và cho biết mệnh đề này đúng hay sai

Hướng dẫn giải

a) +) Mệnh đề P ⇒ Q được phát biểu như sau:

“Nếu tam giác ABC vuông tại A thì độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC”.

Xét tam giác ABC vuông tại A có AM là đường trung tuyến thì AM = $\frac{1}{2}$BC. Do đó mệnh đề P ⇒ Q là mệnh đề đúng.

b) +) Mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu độ dài đường trung tuyến AM bằng nửa độ dài cạnh BC thì tam giác ABC vuông tại A”.

Xét tam giác ABC có đường trung tuyến AM = $\frac{1}{2}$BC.

⇒ AM = MB = MC

⇒ ∆AMB cân tại M

⇒ $\widehat{MAB}=\widehat{MBA}$ hay $\widehat{MAB}=\widehat{CBA}$

Tương tự ta có ∆AMC cân tại M

⇒ $\widehat{MAC}=\widehat{MCA}$ hay $\widehat{MAC}=\widehat{BCA}$

Mà $\widehat{MAB}+\widehat{MAC}=\widehat{BAC}$ nên $\widehat{BAC}=\widehat{BCA}+\widehat{CBA}$

Ta lại có: $\widehat{BAC}+\widehat{BCA}+\widehat{CBA}=180°$

⇒ $\widehat{BAC}=\widehat{BCA}+\widehat{CBA}=90°$

⇒ ∆ABC vuông tại A.

Do đó mệnh đề Q ⇒ P là mệnh đề đúng.

Bài 8. Xét tính đúng sai của mệnh đề

a)$"\forall x\in \mathrm{\mathbb{N}}, x^2⋮6\Rightarrow x⋮6".$

b) Q: "Với mọi giá trị n thuộc tập hợp số nguyên, n² + 1 không chia hết cho 3".

c) P: "Nếu $"\forall x\in \mathrm{\mathbb{N}}, x^2⋮5\Rightarrow x⋮5".$

Hướng dẫn giải

a) Ta có $x^2⋮6\iff \left\{\begin{array}{l}{\mathrm{x}}^2⋮3\\ {\mathrm{x}}^2⋮2\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}⋮3\\ \mathrm{x}⋮2\end{array}\right.\iff \mathrm{x}⋮6.$

Vậy mệnh đề đúng.

b) Mệnh đề phủ định của mệnh đề Q: “∀n ∈ ℕ, n² + 1 không chia hết cho 3” là mệnh đề $\overline{Q}$: “∃n ∈ ℕ, n² + 1 chia hết cho 3”.

Ta xét các trường hợp sau của n:

TH1. n chia hết cho 3: n = 3k (k ∈ ℕ)  

⇒  n² + 1 = 9k² + 1 không chia hết cho 3.

TH2. n chia cho 3 dư 1: n = 3k + 1 (k ∈ ℕ)

⇒  n² + 1 = 9k² + 6k + 1 + 1 =  9k² + 6k + 2 không chia hết cho 3.

TH2. n chia cho 3 dư 2: n = 3k + 2 (k ∈ ℕ)

⇒  n² + 1 = 9k² + 12k + 4 + 1 =  9k² + 12k + 5 không chia hết cho 3.

Suy ra n² + 1 không chia hết cho 3 với mọi số tự nhiên n.

Do đó mệnh đề Q đúng và mệnh đề $\overline{Q}$ sai.

c) Giả sử với $\forall x\in \mathrm{\mathbb{N}}$ và n²$⋮$5 thì n không chia hết cho 5

Vì n không chia hết cho 5 nên n có thể biểu diễn theo một trong các dạng sau: n = 5k$\pm$1 hoặc n = 5k$\pm$2.

Với n = 5k1$\pm 1$ ta có $n^2=25k^2\pm 10k+1$ không chia hết cho 5.

Với n = 5k1$\pm 2$ ta có $n^2=25k^2\pm 20k+4$ không chia hết cho 5.

Vậy mệnh đề trên đúng.

Bài 9. Xét mệnh đề chứa biến: P(x): "x³ - 3x² + 2x = 0". Có bao nhiêu giá trị của biến x để mệnh đề trên là mệnh đề đúng?

Hướng dẫn giải

Ta có x³ - 3x² + 2x = 0 $\iff \left\{\begin{array}{l}x=0\\ x=1\\ x=2\end{array}\right.$. Vậy có ba giá trị của x

2.2. Bài tập trắc nghiệm

Bài 1. Mệnh đề nào sau đây đúng?

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn;

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi hai số đều là số chẵn;

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ;

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Ta thấy tổng của hai số lẻ chẳng hạn như 3 và 5 bằng 8 là số chẵn nên mệnh đề câu A sai.

B. Ta thấy tích của một số lẻ với một số chẵn chẳng hạn như 5 và 2 bằng 10 là số chẵn nên mệnh đề câu B sai.

C. Ta thấy tổng của một số lẻ với một số chẵn chẳng hạn như 5 và 2 bằng 7 là số lẻ nên mệnh đề C sai.

D. Mệnh đề câu D là đúng vì tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. Chẳng hạn 3.5 = 15.

Bài 2. Trong các mệnh đề sau, mệnh đề nào sau đây sai?

A. $\sqrt{2022}$ là một số hữu tỷ;

B. 2022 là một số tự nhiên chẵn;

C. 2022 không phải là số nguyên tố;

D. 2022 chia hết cho 2.

Hướng dẫn giải:

Đáp án đúng là: A.

A. Mệnh đề trên sai vì $\sqrt{2022}$ là số vô tỷ.

B. Vì 2022 là một số tự nhiên chẵn nên mệnh đề trên đúng.

C. Vì số nguyên tố là những số chỉ chia hết cho 1 và chính nó nên 2022 không phải là số nguyên tố. Do đó, mệnh đề trên đúng.

D. Vì 2022 là một số tự nhiên chẵn nên sẽ chia hết cho 2, do đó mệnh đề trên đúng.

Bài 3. Cho các mệnh đề dưới đây:

(1) 24 là số nguyên tố.

(2) Phương trình x² – 5x + 9 = 0 có mấy nghiệm thực phân biệt?

(3) Phương trình x² + 1 = 0 có 2 nghiệm thực phân biệt.

(4) Mọi số nguyên lẻ đều không chia hết cho 2.

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: A.

(1) Vì số nguyên tố là những số chỉ chia hết cho số 1 và chính nó nên 24 không phải là số nguyên tố.

Vì vậy mệnh đề trên là sai.

(2) Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.

(3) Vì phương trình x² + 1 = 0 vô nghiệm nên mệnh đề ở câu b sai.

(4) Mệnh đề trên là đúng vì số lẻ không chia hết cho 2.

Vậy có 1 mệnh đề đúng.

Bài 4. Cho mệnh đề chứa biến P(x): x² – 1 là số lẻ. Xét tính đúng sai của P(2) và P(3).

A. P(2) đúng, P(3) đúng;

B. P(2) sai, P(3) sai;

C. P(2) đúng, P(3) sai;

D. P(2) sai, P(3) đúng.

Hướng dẫn giải:

Đáp án đúng là: C.

+ Thay x = 2 vào P(x) ta được: 2² – 1 = 3.

Vì 3 là số lẻ nên mệnh đề P(x) đúng.

+ Thay x = 3 vào P(x) ta được: 3² – 1 = 8.

Vì 8 là số chẵn nên mệnh đề P(x) sai.

Bài 5. Tìm mệnh đề sai trong các mệnh đề sau:

A. Nếu n là số nguyên chẵn thì n² là số nguyên chẵn;

B. Điều kiện cần và đủ để một số chia hết cho 5 là số đó phải có chữ số tận cùng là 0 hoặc 5;

C. Tổng 3 góc trong của một tam giác bằng 360°;

D. Tam giác có ba cạnh bằng nhau là tam giác đều.

Hướng dẫn giải:

Đáp án đúng là: C.

A. Giả sử n là số nguyên chẵn thì n² = n . n cũng là số nguyên chẵn vì nó là tích của hai số nguyên chẵn.

Suy ra mệnh đề trên đúng.

B. Mệnh đề trên đúng vì điều kiện cần và đủ để một số chia hết cho 5 là số đó phải có chữ số tận cùng là 0 hoặc 5.

Chẳng hạn số 10 có chữ số tận cùng là 0 hay số 15 có chữ số tận cùng là 5 sẽ chia hết cho 5.

C. Vì tổng 3 góc trong của một tam giác bằng 180° nên mệnh đề trên sai.

D. Mệnh đề trên đúng vì nếu một tam giác có ba cạnh bằng nhau thì đó là tam giác đều.

Bài 6. Mệnh đề nào sau đây đúng?

A. ∀x ∈ ℝ, x > x² ;

B. ∀x ∈ ℝ, 4x² + 2x + 1 > 1;

C. ∃x ∈ ℝ, x = x² ;

D. ∃x ∈ ℤ, 25x² – 1 = 0.

Hướng dẫn giải:

Đáp án đúng là: C.

A. Với x = 0 ∈ ℝ ta có: 0 > 0² (vô lý)

Suy ra mệnh đề trên sai.

B. Với x = 0 ∈ ℝ ta có: 4.0² + 2.0 + 1 = 1 > 1 (vô lý).

Suy ra mệnh đề trên sai.

C. Với x = 0 ∈ ℝ ta có: 0 = 0² (đúng)

Do đó mệnh đề trên đúng.

D. Ta có:

25x² – 1 = 0 ⟺ x² = $\frac{1}{25}$

⇒ x = $\frac{1}{5}$ hoặc x = $-\frac{1}{5}$.

Không có số nguyên x ∈ ℤ  nào thỏa mãn phương trình 25x² – 1 = 0 nên mệnh đề trên sai.

Bài 7. Cho mệnh đề chứa biến P(x): x ∈ ℝ: x² + 2 > 12. Mệnh đề nào sau đây đúng?

A. P(2);

B. P(1);

C. P(3);

D. P(4).

Hướng dẫn giải:

Đáp án đúng là: D.

Xét bất phương trình: x² + 2 > 12       (*).

A. Thay x = 2 vào phương trình (*) ta có: 2² + 2 = 6 > 12 (vô lý)

Suy ra mệnh đề trên sai.

B. Thay x = 1 vào phương trình (*) ta có: 1² + 2 = 3 > 12 (vô lý).

Suy ra mệnh đề trên sai.

C. Thay x = 3 vào phương trình (*) ta có: 3² + 2 = 11 > 12 (vô lý).

Suy ra mệnh đề trên sai.

D. Thay x = 4 vào phương trình (*) ta có: 4² + 2 = 18 > 12 (đúng).

Suy ra mệnh đề trên đúng.

Bài 8. Trong các mệnh đề sau, mệnh đề nào sai?

A. Một tứ giác là hình chữ nhật khi và chỉ khi nó có ba góc vuông;

B. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau;

C. Một tam giác có hai cạnh bằng nhau là tam giác cân.

D. Tam giác có ba góc có số đo bằng 60° là tam giác đều.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Mệnh đề trên đúng vì định nghĩa "Một tứ giác là hình chữ nhật khi và chỉ khi nó có ba góc vuông" đúng.

B. Mệnh đề trên sai vì:

Hai tam giác bằng nhau thì suy ra chúng đồng dạng và có một cạnh bằng nhau. Nhưng ngược lại, hai tam giác đồng dạng và có một cạnh bằng nhau thì chưa chắc hai tam giác đó bằng nhau.

C. Mệnh đề trên đúng vì định nghĩa "Một tam giác có hai cạnh bằng nhau là tam giác cân" đúng.

D. Mệnh đề trên đúng vì định nghĩa "Tam giác có ba góc có số đo bằng 60° là tam giác đều" đúng.

Bài 9. Cho mệnh đề đúng sau: "Tất cả mọi người bạn của Trung đều biết bơi". Trong các mệnh đề sau, mệnh đề nào đúng?

A. Bình biết bơi nên Bình là bạn của Trung.

B. An là bạn của Trung nên An không biết bơi.

C. Minh không biết bơi nên Minh không là bạn của Trung.

D. Thành không là bạn của Trung nên Thành không biết bơi.

Hướng dẫn giải:

Đáp án đúng là: C.

A. Bình biết bơi nhưng chưa chắc Bình đã là bạn của Trung nên mệnh đề câu A sai.

B. Vì tất cả mọi người bạn của Trung đều biết bơi nên nếu An là bạn của Trung thì An phải biết bơi nên mệnh đề câu B sai.

C. Vì tất cả mọi người bạn của Trung đều biết bơi nên nếu Minh không biết bơi thì Minh không phải là bạn của Trung nên mệnh đề câu C đúng.

D. Nếu Thành không phải là bạn của Trung thì Thành có thể biết bơi hoặc không nên không thể kết luận Thành không biết bơi, vì vậy mệnh đề câu D sai.

Bài 10. Cho các câu sau đây:

(1) Thời khóa biểu ngày mai là gì vậy?

(2) Một năm có 12 tháng.

(3) Phương trình x² – 4x + 3 = 0 có hai nghiệm dương phân biệt.

(4) x² > x + 1.

Có bao nhiêu câu là mệnh đề đúng?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải:

Đáp án đúng là: B.

+ Câu (1) không phải là mệnh đề vì nó là câu hỏi, vì vậy nó không khẳng định tính đúng sai.

+ Câu (2) là mệnh đề vì nó khẳng định tính đúng sai. Và một năm có 12 tháng là đúng nên mệnh đề trên đúng.

+ Câu (3) là mệnh đề vì nó khẳng định tính đúng sai.

Ta có phương trình x² – 4x + 3 = 0 có hai nghiệm dương phân biệt là x = 1 và x = 3.

Nên mệnh đề trên đúng.

+ Câu (4) là mệnh đề chứa biến vì ta có tập D của các biến x để p(x) đúng hoặc sai vì vậy ta chưa xác định được tính đúng sai của câu trên.

Bài 11: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau.

B. Một tam giác là tam giác vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.

C. Một tam giác là tam giác đều khi và chủ khi nó có hai đường trung tuyến bằng nhau và có một góc bằng 60°.

D. Một tứ giác là hình chữ nhật khi và chỉ khi nó có 3 góc vuông.

Hướng dẫn giải:

Đáp án đúng là: A.

Mệnh đề A: Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau là sai.

* Hai tam giác bằng nhau thì suy ra chúng đồng dạng và có một cạnh bằng nhau.

Ngược lại, hai tam giác đồng dạng và có 1 cạnh bằng nhau thì chưa chắc hai tam giác đó bằng nhau.

Dạng 3: Phủ định một mệnh đề

1. Phương pháp giải

- Để phủ định một mệnh đề ta thêm hoặc bớt từ “không” hoặc “không phải” trước vị ngữ của mệnh đề đó.

- Ta có thể dùng từ thay thế hoặc đặt lại câu có cùng ý nghĩa.

- Mệnh đề phủ định của mệnh đề 

- Mệnh đề phủ định của mệnh đề

- Để phủ định mệnh đề kéo theo P $\Rightarrow$ Q ta hiểu P $\Rightarrow$ Q là ta có Q (x )” nên mệnh đề phủ định là , P(x) ta có $\overline{Q\left(x\right)}$”.

- Phủ định mệnh đề " P" là mệnh đề " không phải ", kí hiệu $\overline{P}$

- Tính chất X thành không X và ngược lại.

- Quan hệ = thành quan hệ $\ne$và ngược lại.

- Quan hệ < thành quan hệ $\ge$và ngược lại.

- Quan hệ > thành quan hệ $\le$và ngược lại.

-

-

- 

- 

Nếu P đúng thì $\overline{P}$ sai, nếu P sai thì $\overline{P}$ đúng.

2. Bài tập tự luyện

2.1. Bài tập tự luận

Bài 1. Nêu mệnh đề phủ định của các mệnh đề sau.

P:" Trong tam giác tổng ba góc bằng 1800"

Q :" 6 không phải là số nguyên tố"

Hướng dẫn giải

Ta có các mệnh đề phủ định là:

$\overline{P}$ :"Trong tam giác tổng ba góc không bằng 1800"

$\overline{Q}$:" 6 là số nguyên tố"

Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau .

a) Mọi hình vuông đều là hình thoi.

b) Có một tam giác cân không phải là tam giác đều.

Hướng dẫn giải

Ta có các mệnh đề phủ định là:

a) Có ít nhất một hình vuông không phải là hình thoi.

b) Mọi tam giác cân đều là tam giác đều.

Bài 3. Lập mệnh đề phủ định của mỗi mệnh đề sau .

a) 

b) 

Hướng dẫn giải

Ta có các mệnh đề phủ định là:

a) 

b) 

Bài 4. Lập mệnh đề phủ định của mỗi mệnh đề sau:

a) 

b)

Hướng dẫn giải

Ta có các mệnh đề phủ định là:

a) 

b) 

Bài 5. Lập mệnh đề phủ định của mỗi mệnh đề sau:

P:“Phương trình x² + 1 = 0 có nghiệm”

Q : “$\forall n\in N, 2n+1$là số lẻ”

Hướng dẫn giải

Ta có các mệnh đề phủ định là:

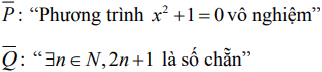
Bài 6. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề 

Hướng dẫn giải

Mệnh đề  là mệnh đề đúng vì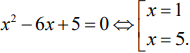 

Phủ định của mệnh đề là mệnh đề 

Bài 9.

a) Phát biểu mệnh đề phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6”.

b) Phát biểu mệnh đề phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.

Hướng dẫn giải

a) Phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6 ” là mệnh đề “Có n chia hết cho 2 và cho 3 mà không chia hết cho 6 ”.

b) Phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau” là mệnh đề “Có hai tam giác bằng nhau mà diện tích của chúng khác nhau” .

Bài 10. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định

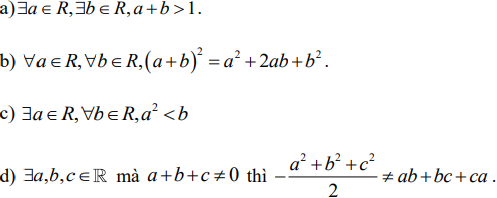
Hướng dẫn giải

a) Phủ định của mệnh đề là 

Mệnh đề phủ định này sai vì với a = 1; b = 1thif a + b = 2 > 1

b) Phủ định của mệnh đề là 

Mệnh đề phủ định này sai.

c) Phủ định của mệnh đề là 

Mệnh đề phủ định này đúng.

d) Phủ định của mệnh đề là 

Mệnh đề phủ định này đúng vì a + b + c = 0 $\iff$(a + b + c)² = 0 $\iff$a² + b² + c² + 2ab + 2ac + 2bc = 0 $\iff -\frac{a^2+b^2+c^2}{2}=ab+bc+ca$

2.2. Bài tập trắc nghiệm

Bài 1. Cho mệnh đề: “∀x ∈ ℝ, x < 3 ⇒ x² < 9”.

Mệnh đề trên được phát biểu như thế nào?

A. Tồn tại số thực x mà nếu số đó bé hơn 3 thì bình phương của nó bé hơn 9;

B. Với mọi số thực x mà nếu số đó bé hơn 3 thì bình phương của nó bé hơn 9;

C. Không có số thực x nào mà nếu số đó bé hơn 3 thì bình phương của nó bé hơn 9;

D. Có duy nhất một số thực x mà nếu số đó bé hơn 3 thì bình phương của nó bé hơn 9.

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có mệnh đề “∀x ∈ ℝ, x < 3 ⇒ x² < 9” được phát biểu như sau: 

“Với mọi số thực x mà nếu số đó bé hơn 3 thì bình phương của nó bé hơn 9”.

Đối chiếu với các đáp án, ta thấy phương án B là hợp lý nhất.

Bài 2. Cho mệnh đề sau: “… x ∈ ℝ, 4x² – 1 = 0”.

Chỗ trống trong mệnh đề trên có thể điền kí hiệu nào dưới đây để mệnh đề đúng?

A. ∀;

B. ∃;

C. Cả hai kí hiệu ∀ và ∃ đều được;

D. Không có kí hiệu nào thỏa mãn.

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có:

4x² – 1 = 0 (*) ⇔ x² = $\frac{1}{4}$ ⇔ x = $\frac{1}{2}$ hoặc x =$-\frac{1}{2}$.

Ta thấy phương trình (*) có hai nghiệm phân biệt, hay nói cách khác phương trình (*) tồn tại hai giá trị của x là x = $\frac{1}{2}$ và x = $-\frac{1}{2}$ thỏa mãn.

Vì vậy ta dùng kí hiệu ∃ cho mệnh đề trên.

Bài 3. Mệnh đề “Mọi số chẵn đều chia hết cho 2” có mệnh đề phủ định là:

A. Mọi số chẵn đều không chia hết cho 2;

B. Có ít nhất một số chẵn chia hết cho 2;

C. Mọi số chẵn đều không chia hết cho 2;

D. Có ít nhất một số chẵn không chia hết cho 2.

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có :

+ Phủ định của “mọi” là “có ít nhất”.

+ Phủ định của “chia hết” là “không chia hết”.

Do đó mệnh đề phủ định của mệnh đề trên là “Có ít nhất một số chẵn không chia hết cho 2”.

Bài 4. Mệnh đề nào sau đây đúng?

A. ∃x ∈ ℤ, x² – 4 = 0;

B. ∀x ∈ ℤ, x² + 1 chia hết cho 3;

C. ∀x ∈ ℤ, x² > x;

D. ∃x ∈ ℤ, x² + 1 = 0.

Hướng dẫn giải:

Đáp án đúng là: A.

A. Ta có:

x² – 4 = 0 (*) ⇔ x² = 4 ⇔ x = 2 hoặc x = – 2.

Ta thấy phương trình (*) có hai nghiệm phân biệt, hay nói cách khác phương trình (*) tồn tại hai giá trị nguyên của x là x = 2 và x = – 2 thỏa mãn.

Do đó mệnh đề ở câu A đúng.

B. Giả sử với x = 0 thì x² + 1 = 0² + 1 = 1 không chia hết cho 3.

Do đó mệnh đề trên dùng kí hiệu “với mọi” là sai.

Vì vậy mệnh đề ở câu B sai.

C. Ta giả sử với x = 0.

⇒ x² = 0² = 0 = x.

Do đó mệnh đề trên dùng kí hiệu “với mọi” là sai.

Vì vậy mệnh đề ở câu C sai.

D. Ta có:

x² + 1 = 0 (**) ⇔ x² = – 1 (vô nghiệm vì x² luôn lớn hơn hoặc bằng 0).

Suy ra không có giá trị nguyên x nào thỏa mãn phương trình (**).

Do đó mệnh đề ở câu D sai.

Bài 5. Cho hai mệnh đề sau:

A: “∀x ∈ ℝ: x² – 4 ≠ 0” ;

B: “∃x ∈ ℝ: x² = x”.

Xét tính đúng sai của hai mệnh đề trên.

A. A đúng, B sai;

B. A sai, B đúng;

C. A đúng, B đúng;

D. A sai, B sai.

Hướng dẫn giải:

Đáp án đúng là: B.

- Xét mệnh đề A, ta có:

x² – 4 = 0 ⇔ x² = 4 ⟺ x = 2 hoặc x = – 2. 

Ta thấy phương trình x² – 4 = 0 có hai nghiệm là x = 2 và x = – 2, hay nói cách khác là có hai giá trị để x² – 4 bằng 0.

Do đó mệnh đề A dùng kí hiệu “với mọi” là sai.

Vậy mệnh đề A sai.

- Xét mệnh đề B, ta có:

x² = x ⇔ x² – x = 0 ⇔ x = 0 hoặc x = 1.

Ta thấy phương trình x² = x có hai nghiệm phân biệt, hay nói cách khác phương trình x² = x tồn tại hai giá trị nguyên của x là x = 0 và x = 1 thỏa mãn.

Do đó mệnh đề B đúng.

Vậy mệnh đề A sai, mệnh đề B đúng.

Bài 6. Kí hiệu X là tập hợp tất cả các bạn học sinh x trong lớp 10A1, P(x) là mệnh đề chứa biến “x đạt học sinh giỏi”. Mệnh đề “∃x ∈ X, P(x)” khẳng định rằng:

A. Tất cả các bạn học sinh trong lớp 10A1 đều đạt học sinh giỏi;

B. Bất cứ ai đạt học sinh giỏi đều học lớp 10A1;

C. Có một số bạn học lớp 10A1 đạt học sinh giỏi;

D. Tất cả các bạn học sinh trong lớp 10A1 đều không đạt học sinh giỏi.

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có mệnh đề “∃x ∈ X, P(x)” được phát biểu như sau:

“Có một số bạn học lớp 10A1 đạt học sinh giỏi”.

Đối chiếu các đáp án, ta thấy đáp án C là phù hợp nhất.

Bài 7. Mệnh đề “∀x ∈ ℤ, x² + 1 > 0” được phát biểu là:

A. Với mọi số nguyên x, ta có x² + 1 luôn lớn hơn 0;

B. Tồn tại duy nhất một số nguyên x để x² + 1 luôn lớn hơn 0;

C. Tồn tại ít nhất một số nguyên x để x² + 1 luôn lớn hơn 0;

D. Không có số nguyên nào thỏa mãn bất đẳng thức x² + 1 > 0.

Hướng dẫn giải:

Đáp án đúng là: A.

Mệnh đề “∀x ∈ ℤ, x² + 1 > 0” được phát biểu như sau:

Với mọi số nguyên x, ta có x² + 1 luôn lớn hơn 0.

Đối chiếu các đáp án, ta thấy đáp án A là phù hợp nhất.

Bài 8. Mệnh đề nào sau đây sai?

A. ∀x ∈ ℕ, x ≤ 2x;

B. ∀x ∈ ℝ, $\sqrt{x}$ ≥ 0;

C. ∃x ∈ ℕ, x² = x;

D. ∀x ∈ ℝ, x > 0.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Mệnh đề “∀x ∈ ℕ, x ≤ 2x” được phát biểu như sau:

“Với mọi số tự nhiên x, ta luôn có bất phương trình x ≤ 2x”.

Ta thấy mệnh đề này đúng vì mọi số tự nhiên x luôn thỏa mãn x ≤ 2x.

B. Mệnh đề “∀x ∈ ℝ, $\sqrt{x}$ ≥ 0” được phát biểu như sau:

“Với mọi số thực x thì căn bậc hai số học của số đó luôn lớn hơn hoặc bằng 0”.

Mệnh đề này đúng vì căn bậc hai số học của một số luôn lớn hơn hoặc bằng 0.

C. Mệnh đề “∃x ∈ ℕ, x² = x” được phát biểu như sau:

“Tồn tại ít nhất một số tự nhiên x để bình phương của một số bằng chính số đó”.

Ta có:

x² = x ⇔ x² – x = 0 ⇔ x = 0 hoặc x = 1.

Ta thấy phương trình x² = x có hai nghiệm phân biệt, hay nói cách khác phương trình x² = x tồn tại hai giá trị của x là x = 0 và x = 1 thỏa mãn, chính là tồn tại số tự nhiên để bình phương của nó bằng chính nó.

Do đó mệnh đề ở câu C đúng.

D. Mệnh đề “∀x ∈ ℝ, x > 0” được phát biểu như sau:

“Mọi số thực x luôn luôn lớn hơn 0”.

Mệnh đề này sai vì số thực x có thể âm hoặc bằng 0.

Bài 9. Cho mệnh đề : “∀x ∈ ℝ, x³ – 5x + 6 ≥ 0”.

Mệnh đề phủ định của mệnh đề trên là:

A. ∃x ∈ ℝ, x³ – 5x + 6 ≥ 0;

B. ∀x ∈ ℝ, x³ – 5x + 6 < 0;

C. ∀x ∉ ℝ, x³ – 5x + 6 ≥ 0;

D. ∃x ∈ ℝ, x³ – 5x + 6 < 0.

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

+ Phủ định của “∀” là “∃”.

+ Phủ định của “≥” là “<”.

Do đó mệnh đề phủ định của mệnh đề đã cho là: “∃x ∈ ℝ, x³ – 5x + 6 < 0”.

Bài 10. Cho các mệnh đề sau:

(1) ∀x ∈ ℝ, |x| > 1 ⇒ x > 1.

(2) ∃x ∈ ℤ, 2x² – 8 = 0.

(3) ∀x ∈ ℕ, 2^x + 1 là số nguyên tố.

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải:

Đáp án đúng là: B.

(1) Thay x = – 1 vào mệnh đề (1) ta có:

|– 1| > 1 ⇒ – 1 > 1 (vô lý).

Do đó mệnh đề (1) sai.

(2) Ta có:

2x² – 8 = 0 (*) ⇔ 2x² – 8 ⇔ x² = 4 ⇔ x = 2 hoặc x = – 2.

Ta thấy phương trình (*) có hai nghiệm phân biệt, hay nói cách khác phương trình (*) tồn tại hai giá trị nguyên của x là x = 2 và x = – 2 thỏa mãn.

Do đó mệnh đề (2) đúng.

(3) Thay x = 3 vào mệnh đề (3) ta có:

2³ + 1 = 8 + 1 = 9.

Ta thấy 9 không phải là số nguyên tố vì số nguyên tố là số chỉ chia hết cho 1 và chính nó nên mệnh đề (3) sai.

Bài 11: Xét mệnh đề P: "∀x ∈ R, x² + 1 > 0". Mệnh đề phủ định P_ của mệnh đề P là:

Hướng dẫn giải:

Đáp án đúng là: B.

Chọn đáp án B

Dạng 4: Mệnh đề kéo theo. Mệnh đề đảo. Mệnh đề tương đương

1. Phương pháp giải

a. Mệnh đề kéo theo

- Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo.

Kí hiệu là P ⇒ Q.

- Mệnh đề P ⇒ Q còn được phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.

- Tính đúng, sai của mệnh đề kéo theo được xác định như sau:

Mệnh đề P ⇒ Q chỉ sai khi P đúng và Q sai.

Lưu ý: Để xét tính đúng sai của mệnh đề P ⇒ Q, ta chỉ cần xét trường hợp P đúng. Khi đó, nếu Q đúng thì mệnh đề đúng, nếu Q sai thì mệnh đề sai.

- Phương pháp xét tính đúng sai của mệnh đề P ⟹ Q

- Quan sát xem P, Q đúng hay sai

- Khi đó P ⟹ Q rơi vào mẫu nào trong 4 mẫu sau

1. Đ ⟹ S→Sai

2. Đ ⟹ Đ

3. 𝐒 ⟹ Đ

4. 𝐒 ⟹ 𝐒 →Đúng

Đặc biệt: Có hai trường hợp mà chỉ cần nhìn vào một trong hai mệnh đề P hoặc Q ta sẽ biết (P ⟹ Q) luôn đúng: TH1: P sai. TH2: Q đúng.

- Chú ý: $\overline{P\Rightarrow Q}$ chính là P ∩ Q̅.

- Trong toán học, định lý là mệnh đề đúng.

- Khi mệnh đề P ⇒ Q là định lý, ta nói:

P là giả thiết, Q là kết luận của định lý;

P là điều kiện đủ để có Q;

Q là điều kiện cần để có P.

b. Mệnh đề đảo. Mệnh đề tương đương

- Cho mệnh đề kéo theo P ⇒ Q. Mệnh đề Q ⇒ P được gọi là mệnh đề đảo của mệnh đề P ⇒ Q.

- Để xác định mệnh đề đảo, ta chỉ cần đảo vị trí hai mệnh đề P và Q với nhau.

- Cho hai mệnh đề P và Q. Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng thì ta nói P và Q là hai mệnh đề tương đương.

Kí hiệu P ⇔ Q và có thể đọc theo một số cách sau:

+ P tương đương Q;

+ P là điều kiện cần và đủ để có Q;

+ P nếu và chỉ nếu Q;

+ P khi và chỉ khi Q.

- Cách xét tính đúng, sai của mệnh đề tương đương:

Mệnh đề P ⇔ Q chỉ đúng khi cả hai mệnh đề kéo theo P ⟹ Q và Q ⟹ P đều đúng. Nói cách khác mệnh đề P ⇔ Q đúng nếu cả hai mệnh đề P và Q cùng đúng hoặc cùng sai.

2. Bài tập tự luyện

2.1. Bài tập tự luận

Bài 1. Lập mệnh đề P$\Rightarrow$Q và xét tính đúng sau của nó, với 

Hướng dẫn giải

Ta có mệnh đề P$\Rightarrow$Q là: 

Vì P sai (và Q sai) nên mệnh đề P$\Rightarrow$Q là mệnh đề đúng.

Bài 2. Phát biểu mệnh đề đảo của mệnh đề “Nếu A = 90^o thì $△$ABC là tam giác vuông” và xét tính đúng sai của nó.

Hướng dẫn giải

Ta có mệnh đề P$\Rightarrow$Q: “Nếu A = 90^o thì $△$ABC là tam giác vuông”

Mệnh đề đảo của mệnh đề trên là Q$\Rightarrow$P: “ Nếu $△$ABC là tam giác vuông thì A = 90^o”.

Mệnh đề Q$\Rightarrow$P là mệnh đề sai, ví dụ trường hợp $△$ABC vuông tại B .

Bài 3. Cho mệnh đề P:" 2 < 3 ",Q :" - 4 < - 6". Lập mệnh đề P$\Rightarrow$Q và xét tính đúng sai của nó.

Hướng dẫn giải

Mệnh đề sai.

Bài 4. Giả sử ABC là một tam giác đã cho. Lập mệnh đề P$\Rightarrow$Q và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng với P: "Góc A bằng 90^o ", Q:" BC² = AB² + AC² ".

Hướng dẫn giải

 

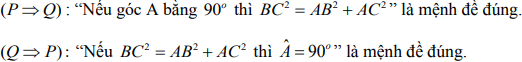
Bài 5. Trên một hòn đảo, tôi đã gặp ba người A, B và C, một người là hiệp sĩ, một người khác là kẻ bất lương và người kia là gián điệp. Người hiệp sĩ luôn nói sự thật, kẻ bất lương luôn luôn nói dối và gián điệp có thể nói dối hoặc nói sự thật.

A nói: "Tôi là hiệp sĩ."

B nói, "Tôi là kẻ bất lương."

C nói: "Tôi là gián điệp."

Hỏi ai là gián điệp?

Hướng dẫn giải

Do tính đúng sai nên để xác định kết quả nhanh nhất, ta sẽ xét hiệp sĩ và gián điệp.

Nếu A nói thật

⟹ A là hiệp sĩ.

⟹ B hoặc C là kẻ bất lương.

Nếu B là kẻ bất lương ⟹ B nói dối ⟹ Mâu thuẫn

Nếu C là kẻ bất lương ⟹ C nói dối ⟹ Thỏa mãn

Vậy A là hiệp sĩ, C là kẻ bất lương và B là gián điệp cần tìm

Bài 6. Phát biểu mệnh đề đảo của định lý: “Trong một tam giác cân, các đường cao ứng với các cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao?

Hướng dẫn giải

Mệnh đề đảo: “Trong tam giác, các đường cao ứng với các cạnh bên bằng nhau thì tam giác đó là tam giác cân”.

Mệnh đề đảo trên đúng.

Bài 7. Ba anh em An, Bình, Vinh ngồi làm bài xung quanh một cái bàn được trải khăn mới. Khi phát hiện có vết mực, bà hỏi thì các cháu lần lượt trả lời:

An: “Em Vinh không làm đổ mực, đấy là do em Bình.”

Bình: “Em Vinh làm đổ mực, anh An không làm đổ mực”.

Vinh: “Theo cháu, Bình không làm đổ mực, còn cháu hôm nay không chuẩn bị bài”.

Biết rằng trong 3 em thì có 2 em nói đúng, 1 em nói sai. Hỏi ai làm đổ mực?

Hướng dẫn giải

Nếu An nói đúng thì Bình là người làm đổ, suy ra Bình nói sai, theo đề bài ta có Vinh nói đúng.

Nếu Vinh nói đúng thì Bình không làm đổ mực. Suy ra mâu thuẫn.

Nếu Bình nói đúng, Vinh làm đổ mực thì An nói sai. Dẫn đến Vinh nói đúng. Suy ra thỏa mãn.

Vậy Vinh làm đổ mực.

Bài 8. Ếch hay cóc?

Trong một đầm lầy ma thuật, có hai loài lưỡng cư biết nói: cóc luôn luôn nói đúng và ếch luôn luôn nói sai.

Bốn loài lưỡng cư, Brian, Chris, LeRoy và Mike sống cùng nhau trong đầm lầy này và chúng đưa ra những tuyên bố sau:

Brian: "Mike và tôi là những loài khác nhau."

Chris: "LeRoy là một con ếch."

LeRoy: "Chris là một con ếch."

Mike: "Trong bốn người chúng tôi, ít nhất hai người là cóc."

Có bao nhiêu loài lưỡng cư là ếch?

Hướng dẫn giải

Cách 1: Trình bày lời văn:

Giả sử Brian là cóc (nói thật)

⟹ Mike là ếch (nói dối)

⟹ Chỉ có 1 con là ếch trong 4 con. Mà Mike đã là ếch

⟹ LeRoy và Chris là đều cóc (nói thật)

Nhưng Chris nói LeRoy là ếch ⟹ mâu thuẫn

Vậy Brian nói dối (là Ếch)

⟹ Brian và Mike cùng là loài ếch (nói dối)

⟹ Chỉ có 1 con cóc và 3 con còn lại là ếch (*)

• Nếu Chris là Cóc (nói thật) ⟹ LeRoy là ếch (nói dối) ⟹ Thỏa mãn (*)

• Nếu LeRoy là Cóc (nói thật) ⟹ Chris là ếch (nói dối) ⟹ Thỏa mãn (*)

Vậy có 3 loài lưỡng cư là ếch.

Cách 2: Dùng bảng

Kí hiệu: Cóc : x

Ếch: o

Vậy có 3 loài lưỡng cư là ếch.

2.2. Bài tập trắc nghiệm

a. Mệnh đề kéo theo

Bài 1. Cho hai mệnh đề  P: “x là số chẵn” và Q: “x chia hết cho 2”.

Phát biểu mệnh đề P kéo theo Q.

A. Hoặc x là số chẵn hoặc x chia hết cho 2;

B. Nếu x là số chẵn thì x chia hết cho 2;

C. Nếu x chia hết cho 2 thì x là số chẵn;

D. x là số chẵn và x chia hết cho 2.

Hướng dẫn giải:

Đáp án đúng là: B.

Vì mệnh đề kéo theo được phát biểu dưới dạng là “Nếu P thì Q”.

Nên mệnh đề P kéo theo Q là “Nếu x là số chẵn thì x chia hết cho 2”.

Bài 2. Cho a, b là hai số tự nhiên. Mệnh đề kéo theo nào sau đây đúng?

A. Nếu a, b là số lẻ thì a + b là số lẻ;

B. Nếu a, b là số chẵn thì a.b là số chẵn;

C. Nếu a chẵn, b lẻ thì a.b là số lẻ;

D. Nếu a lẻ, b chẵn thì a + b là số chẵn.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Giả sử a = 3, b = 5 đều là số lẻ.

Ta có a + b = 3 + 5 = 8.

Mà 8 là số chẵn nên mệnh đề ở câu A sai.

B. Ta thấy nếu a, b là số chẵn thì a.b là số chẵn là đúng.

Vì tích của hai số chẵn luôn là một số chẵn.

C. Giả sử a = 6 là số chẵn, b = 1 là số lẻ.

Ta có: a.b = 6.1 = 6.

Mà 6 là số chẵn nên mệnh đề ở câu C sai.

D. Giả sử a = 3 là số lẻ, b = 6 là số chẵn.

Ta có: a + b = 3 + 6 = 9.

Mà 9 là số lẻ nên mệnh đề câu D sai.

Bài 3. Mệnh đề nào sau đây đúng?

A. ∀x ∈ ℝ, x < 0 ⇒ x² < 0;

B. ∀x ∈ ℝ, x > – 1 ⇒ x² > 0;

C. ∀x ∈ ℝ, x > 0 ⇒ x² > x;

D. ∀x ∈ ℝ, x < 0 ⇒ x² > 0.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Với  x ∈ ℝ, x < 0;

Giả sử x = – 2 ⇒ x² = (– 2)² = 4 > 0.

Suy ra mệnh đề câu A sai.

B. Với  x ∈ ℝ, x > – 1;

Giả sử x = 0 > – 1 ⇒ x² = 0 > 0 là sai.

Do đó mệnh đề ở câu B sai.

C. Với x ∈ ℝ, x > 0;

Giả sử x = 1 ⇒ x² = 1² = 1.

⇒ x = x².

Do đó mệnh đề câu C sai.

D. Ta thấy mệnh đề ở câu D đúng vì với mọi x < 0, ta luôn có x² > 0 (bình phương của một số âm luôn là một số dương).

Ví dụ: x = – 2 ⇒ x² = (– 2)² = 4 > 0.

Bài 4. Cho các mệnh đề kéo theo dưới đây:

(1) “Nếu tam giác ABC vuông tại A thì AB² + AC² = BC²”.

(2) “Nếu ABCD là hình thoi thì ABCD cũng là hình vuông”.

(3) “Tam giác ABC đều thì tam giác ABC có AB = AC”.

Có bao nhiêu mệnh đề đúng?

A. 0;

B. 1;

C. 2;

D. 3;

Hướng dẫn giải:

Đáp án đúng là: C.

- Theo định lý Pythagore thì trong tam giác vuông, tổng các bình phương hai cạnh góc vuông bằng bình phương cạnh huyền.

Áp dụng cho tam giác ABC vuông tại A, ta có: AB² + AC² = BC².

Do đó mệnh đề (1) đúng.

- Ta có nếu ABCD là hình vuông thì ABCD cũng là hình thoi, nhưng ngược lại, một tứ giác là hình thoi thì nó chưa chắc đã là hình vuông.

Do đó mệnh đề (2) sai.

- Mệnh đề (3) đúng vì tam giác đều có ba cạnh bằng nhau.

Vậy có hai mệnh đề đúng.

Bài 5. Cho ba mệnh đề như sau:

A: “ABCD là hình chữ nhật”.

B: “AB = CD”.

C: “ABCD là hình bình hành”.

Mệnh đề nào sau đây sai?

A. “A ⇒ B”;

B. “A ⇒ C”;

C. “B ⇒ C”;

D. “C ⇒ B”;

Hướng dẫn giải:

Đáp án đúng là: C.

A. Ta có mệnh đề A ⇒ B được phát biểu như sau:

“Nếu ABCD là hình chữ nhật thì AB = CD”.

Vì hình chữ nhật có hai cạnh đối bằng nhau nên AB = CD.

Do đó mệnh đề kéo theo ở câu A đúng.

B. Ta có mệnh đề A ⇒ C được phát biểu như sau:

“Nếu ABCD là hình chữ nhật thì ABCD là hình bình hành”.

Do một tứ giác là hình chữ nhật thì nó cũng là hình bình hành nên mệnh đề kéo theo ở câu B đúng.

C. Ta có mệnh đề B ⇒ C được phát biểu như sau:

“Nếu AB = CD thì ABCD là hình bình hành”.

Mệnh đề này sai do một tứ giác là hình bình hành khi và chỉ khi nó có hai cặp cạnh đối bằng nhau. Do đó chỉ có AB = CD thì chưa đủ để kết luận ABCD là hình bình hành.

D. Ta có mệnh đề C ⇒ B được phát biểu như sau:

“Nếu ABCD là hình bình hành thì AB = CD”.

Vì hình bình hành có hai cặp cạnh đối bằng nhau, nên ABCD là hình bình hành thì AB = CD.

Do đó mệnh đề kéo theo ở câu D đúng.

Bài 6. Mệnh đề nào dưới đây đúng?

A. “Nếu (– 3) > (– 2) thì (– 3)² > (– 2)²”;

B. “Nếu 3 là số lẻ thì 3 chia hết cho 2”; 

C. “Nếu 15 chia hết cho 9 thì 18 chia hết cho 3”;

D. “Nếu 3 chia hết cho 1 và chính nó thì 3 là số nguyên tố”.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Ta thấy mệnh đề “(– 3) > (– 2)” sai do (– 3) < (– 2).

Theo lý thuyết ta có “Để xét tính đúng sai của mệnh đề P ⇒ Q, ta chỉ cần xét trường hợp P đúng” nên nếu mệnh đề P sai thì ta xem mệnh đề đó sai và ta không cần xét mệnh đề Q nữa.

Do đó mệnh đề ở câu A sai.

B. Với mệnh đề kéo theo ở câu B ta có:

Mệnh đề “3 là số lẻ” là đúng, tuy nhiên mệnh đề “3 chia hết cho 2” sai.

Theo lý thuyết “Mệnh đề P ⇒ Q sai khi P đúng và Q sai”

Nên mệnh đề ở câu B sai.

C. Xét mệnh đề kéo theo ở câu C ta có:

Mệnh đề “15 chia hết cho 9” là sai.

Giải thích tương tự câu A, ta có mệnh đề câu C sai.

D. Đặt P: “3 chia hết cho 1 và chính nó”, Q: “3 là số nguyên tố”.

Ta thấy khi P đúng thì Q cũng đúng nên mệnh đề P ⇒ Q đúng.

Bài 7. Cho hai mệnh đề  P: “x chia hết cho 9” và Q: “x chia hết cho 3”.

Phát biểu mệnh đề P kéo theo Q nào dưới đây là sai?

A. Nếu x chia hết cho 9 thì x chia hết cho 3;

B. x chia hết cho 9 suy ra x chia hết cho 3;

C. x chia hết cho 9 kéo theo x chia hết cho 3;

D. x chia hết cho 3 là điều kiện đủ để x chia hết cho 9.

Hướng dẫn giải:

Đáp án đúng là: D.

Đối với mệnh đề kéo theo P ⇒ Q, ta có một số cách phát biểu như sau:

+ Nếu P thì Q;

+ P kéo theo Q;

+ P suy ra Q;

+ P là giả thiết, Q là kết luận của định lý;

+ P là điều kiện đủ để có Q;

+ Q là điều kiện cần để có P.

Ta thấy mệnh đề ở câu D được kí hiệu là “Q là điều kiện đủ để có P”.

Cách phát biểu trên không nằm trong mấy cách phát biểu ở lý thuyết nên mệnh đề kéo theo ở câu D sai.

Bài 8. Trong các mệnh đề sau, mệnh đề nào không phải là định lý?

A. Điều kiện đủ để một số nguyên dương x tận cùng bằng 5 là số đó chia hết cho 5;

B. Điều kiện đủ để diện tích hai tam giác bằng nhau là hai tam giác ấy bằng nhau;

C. Điều kiện đủ để trong mặt phẳng hai đường song song với nhau là hai đường thẳng ấy cùng vuông góc với đường thẳng thứ 3;

D. Điều kiện đủ để hai đường chéo của một tứ giác vuông góc với nhau là tứ giác ấy là hình thoi.

Hướng dẫn giải:

Đáp án đúng là: A.

A. Ta thấy câu A vô lý vì để một số nguyên dương x tận cùng là 5 thì nó không cần có điều kiện là số đó phải chia hết cho 5, vì một số chia hết cho 5 có tận cùng là 0 hoặc 5 nên mệnh đề ở câu A sai.

Do đó câu A không phải là định lý.

B. Đặt P: “Hai tam giác bằng nhau”, Q: “Diện tích của hai tam giác ấy bằng nhau”.

Xét mệnh đề P ⇒ Q “Nếu hai tam giác bằng nhau thì diện tích của hai tam giác ấy bằng nhau” là đúng.

Mà mệnh đề P ⇒ Q  trên có thể viết lại là:

Điều kiện đủ của Q là P (là mệnh đề ở câu B).

Do đó mệnh đề ở câu B đúng và đó là định lý.

C. Đặt P: “Hai đường thẳng cùng song song với đường thẳng thứ 3”, Q: “Hai đường thẳng ấy song song với nhau”.

Xét mệnh đề P ⇒ Q “Nếu hai đường thẳng cùng song song với đường thẳng thứ 3 thì hai đường thẳng ấy song song với nhau” là đúng.

Mà mệnh đề P ⇒ Q  trên có thể viết lại là:

Điều kiện đủ của Q là P (là mệnh đề ở câu C).

Do đó mệnh đề ở câu C đúng và đó là định lý.

D. Đặt P: “Một tứ giác là hình thoi”, Q: “Hai đường chéo của tứ giác ấy vuông góc với nhau”.

Xét mệnh đề P ⇒ Q “Nếu một tứ giác là hình thoi thì hai đường chéo của tứ giác ấy vuông góc với nhau” là đúng.

Mà mệnh đề P ⇒ Q  trên có thể viết lại là:

Điều kiện đủ của Q là P (là mệnh đề ở câu D).

Do đó mệnh đề ở câu D đúng và đó là định lý.

Bài 9. Trong các mệnh đề sau, mệnh đề nào là một định lý?

A. Nếu một tứ giác là hình chữ nhật thì tứ giác đó có bốn cạnh bằng nhau;

B. Nếu một số tự nhiên tận cùng là 5 thì số đó chia hết cho 5;

C. Nếu một tự nhiên chia hết cho 3 thì nó chia hết cho 9;

D. Nếu một tứ giác có hai đường chéo vuông góc với nhau thì tứ giác đó là hình thoi.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Vì hình chữ nhật có hai cặp cạnh đối bằng nhau nên mệnh đề ở câu A sai.

Do đó mệnh đề trên không phải là định lý.

B. Mệnh đề ở câu B đúng do dấu hiệu để một số chia hết cho 5 là số đó có chữ số tận cùng là 0 hoặc 5.

Vì vậy mệnh đề câu B là định lý.

C. Ta có một số chia hết cho 9 thì nó cũng chia hết cho 3, tuy nhiên một số chia hết cho 3 thì nó chưa chắc chia hết cho 9.

Chẳng hạn số 3 chia hết cho 3 nhưng nó không chia hết cho 9.

Nên mệnh đề ở câu C sai và nó không phải là định lý.

D. Mệnh đề ở câu D sai do một tứ giác có hai đường chéo vuông góc với nhau thì chưa chắc nó đã là hình thoi.

Vì vậy mệnh đề trên không phải là định lý.

Bài 10. Cho mệnh đề kéo theo sau: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”.

Mệnh đề trên không thể viết là:

A. Một tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo bằng nhau;

B. Một tứ giác là hình thang cân là điều kiện đủ để tứ giác đó có hai đường chéo bằng nhau;

C. Tứ giác có hai đường chéo bằng nhau là điều kiện cần để một tứ giác là hình thang cân;

D. Tứ giác có hai đường chéo bằng nhau là điều kiện đủ để một tứ giác là hình thang cân.

Hướng dẫn giải:

Đáp án đúng là: D.

Đối với mệnh đề kéo theo P ⇒ Q, ta có một số cách phát biểu như sau:

+ Nếu P thì Q;

+ P kéo theo Q;

+ P là giả thiết, Q là kết luận của định lý;

+ P là điều kiện đủ để có Q;

+ Q là điều kiện cần để có P.

Xét mệnh đề kéo theo “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”, ta có:

Đặt P: “Một tứ giác là hình thang cân”, Q: “Tứ giác đó có hai đường chéo bằng nhau”.

Ta viết lại các mệnh đề ở các đáp án như sau:

A. P kéo theo Q.

B. P là điều kiện đủ để có Q.

C. Q là điều kiện cần để có P.

D. Q là điều kiện đủ để có P.

Ta thấy cách phát biểu ở câu D không nằm trong mấy cách phát biểu ở lý thuyết nên mệnh đề kéo theo ở câu D sai.

b. Mệnh đề đảo. Mệnh đề tương đương. Điều kiện cần và đủ

Bài 1. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu một tứ giác đó là hình vuông thì tứ giác đó có bốn cạnh bằng nhau;

B. Nếu một tứ giác là hình thoi thì tứ giác đó có bốn cạnh bằng nhau;

C. Nếu một tứ giác là hình chữ nhật thì tứ giác đó có hai cặp cạnh đối bằng nhau;

D. Nếu một tứ giác là hình thoi thì tứ giác đó có hai đường chéo vuông góc với nhau.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Ta có:

P: “Một tứ giác là hình vuông”.

Q: “Tứ giác đó có bốn cạnh bằng nhau”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một tứ giác có bốn cạnh bằng nhau thì tứ giác đó là hình vuông”.

Ta thấy mệnh đề trên sai do một tứ giác có bốn cạnh bằng nhau thì nó có thể là hình thoi chứ chưa chắc là hình vuông.

B. Ta có:

P: “Một tứ giác là hình thoi”.

Q: “Tứ giác đó có bốn cạnh bằng nhau”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một tứ giác có bốn cạnh bằng nhau thì tứ giác đó là hình thoi”.

Ta thấy mệnh đề đúng vì một tứ giác có bốn cạnh bằng nhau thì nó là hình thoi theo định nghĩa hình thoi.

C. Ta có:

P: “Một tứ giác là hình chữ nhật”.

Q: “Tứ giác đó có hai cặp cạnh đối bằng nhau”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một tứ giác có hai cặp cạnh đối bằng nhau thì tứ giác đó là hình chữ nhật”.

Ta thấy mệnh đề trên sai do một tứ giác có hai cặp cạnh đối bằng nhau thì nó có thể là hình bình hành chứ chưa chắc là hình chữ nhật.

D. Ta có:

P: “Một tứ giác là hình thoi”.

Q: “Tứ giác đó có hai đường chéo vuông góc với nhau ”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một tứ giác có hai đường chéo vuông góc với nhau thì tứ giác đó là hình thoi”.

Ta thấy mệnh đề trên sai do một tứ giác có hai đường chéo vuông góc với nhau thì nó chưa chắc là hình thoi.

Bài 2. Cho hai mệnh đề sau:

P: “Hai số nguyên dương m, n đều không chia hết cho 9”.

Q: “Tích m.n không chia hết cho 9”.

Phát biểu mệnh đề P ⇔ Q.

A. Nếu hai số nguyên dương m, n đều không chia hết cho 9 thì tích m.n không chia hết cho 9;

B. Hai số nguyên dương m, n đều không chia hết cho 9 và tích m.n không chia hết cho 9;

C. Hai số nguyên dương m, n đều không chia hết cho 9 khi và chỉ khi tích m.n không chia hết cho 9;

D. Hai số nguyên dương m, n đều không chia hết cho 9 là điều kiện đủ để tích m.n không chia hết cho 9.

Hướng dẫn giải:

Đáp án đúng là: C.

Với:

P: “Hai số nguyên dương m, n đều không chia hết cho 9”.

Q: “Tích m.n không chia hết cho 9”.

Ta có thể phát biểu mệnh đề P ⇔ Q như sau:

“Hai số nguyên dương m, n đều không chia hết cho 9 khi và chỉ khi tích m.n không chia hết cho 9”.

Bài 3. Cho mệnh đề: “x² – 1 chia hết cho 24 khi và chỉ khi x là một số nguyên tố lớn hơn 3”.

Mệnh đề trên không thể viết lại thành mệnh đề nào sau đây?

A. “x² – 1 chia hết cho 24 tương đương với x là một số nguyên tố lớn hơn 3”;

B. “x² – 1 chia hết cho 24 là điều kiện cần và đủ để x là một số nguyên tố lớn hơn 3”;

C. “x² – 1 chia hết cho 24 nếu và chỉ nếu x là một số nguyên tố lớn hơn 3”;

D. “x² – 1 chia hết cho 24 là điều kiện đủ để x là một số nguyên tố lớn hơn 3”

Hướng dẫn giải:

Đáp án đúng là: D.

Xét mệnh đề: “x² – 1 chia hết cho 24 khi và chỉ khi x là một số nguyên tố lớn hơn 3”.

Đặt:

P: “x² – 1 chia hết cho 24”.

Q: “x là một số nguyên tố lớn hơn 3”.

Ta viết lại các mệnh đề ở đáp án như sau:

A. P tương đương với Q.

B. P là điều kiện cần và đủ để có Q.

C. P nếu và chỉ nếu Q.

D. P là điều kiện đủ để có Q.

Đối với mệnh đề P ⇔ Q, ta có thể phát biểu theo một số cách sau:

+ P tương đương Q;

+ P là điều kiện cần và đủ để có Q;

+ P nếu và chỉ nếu Q;

+ P khi và chỉ khi Q.

Ta thấy cách phát biểu ở câu D không nằm trong mấy cách phát biểu ở lý thuyết nên mệnh đề tương đương ở câu D sai.

Bài 4. Trong các mệnh đề tương đương sau, mệnh đề nào sai?

A. “ABC là tam giác đều ⇔ ABC là tam giác cân”;

B. “ABC là tam giác đều ⇔ tam giác ABC có ba cạnh bằng nhau”;

C. “ABC là tam giác đều ⇔ tam giác ABC cân và có một góc bằng 60°”;

D. “ABC là tam giác đều ⇔ tam giác ABC có hai góc bằng 60°”;

Hướng dẫn giải:

Đáp án đúng là: A.

A. Xét mệnh đề: “ABC là tam giác đều ⇒ ABC là tam giác cân”.

Ta thấy mệnh đề trên đúng do một tam giác là tam giác đều thì nó cũng là tam giác cân.

- Xét mệnh đề đảo: “ABC là tam giác cân ⇒ ABC là tam giác đều”.

Ta thấy mệnh đề này sai vì tam giác cân là tam giác có hai cạnh bằng nhau, tuy nhiên điều kiện để một tam giác là tam giác đều khi nó có ba cạnh. Do đó một tam giác cân chưa chắc đã là tam giác đều.

Do đó mệnh đề ở câu A sai.

B. Xét mệnh đề: “ABC là tam giác đều ⇒ tam giác ABC có ba cạnh bằng nhau”.

Vì một tam giác là tam giác đều thì nó có ba cạnh bằng nhau nên mệnh đề trên đúng.

- Xét mệnh đề đảo: “Tam giác ABC có ba cạnh bằng nhau ⇒ ABC là tam giác đều”.

Ta thấy mệnh đề này đúng vì nếu một tam giác có ba cạnh bằng nhau thì tam giác đó đều.

Do đó mệnh đề ở câu B đúng.

C. Xét mệnh đề: “ABC là tam giác đều ⇒ tam giác ABC cân và có một góc bằng 60°”.

Ta thấy mệnh đề này đúng vì đó là tính chất của một tam giác đều.

- Xét mệnh đề đảo: “Tam giác ABC cân và có một góc bằng 60° ⇒ ABC là tam giác đều”.

Mệnh đề này đúng vì một trong những dấu hiệu của một tam giác đều là tam giác đó cân và có một góc bằng 60°.

Do đó mệnh đề ở câu C đúng.

D. Xét mệnh đề: “ABC là tam giác đều ⇒ tam giác ABC có hai góc bằng 60°”.

Mệnh đề này đúng vì tam giác đều có ba góc bằng 60°.

Xét mệnh đề đảo: “Tam giác ABC có hai góc bằng 60° ⇒ ABC là tam giác đều”.

Mệnh đề này cũng đúng vì một tam giác có hai góc bằng 60° là một dấu hiệu của tam giác đều.

Do đó mệnh đề ở câu D đúng.

Bài 5. Cho các mệnh đề sau đây:

(1) “Nếu một số tự nhiên n chia hết cho 24 thì n chia hết cho 4 và 6”;

(2) “Nếu mỗi số tự nhiên a, b chia hết cho 11 thì tổng hai số a và b chia hết cho 11”;

(3) “Nếu một tứ giác là hình thang cân thì nó có hai đường chéo bằng nhau”.

Có bao nhiêu mệnh đề có mệnh đề đảo của nó đúng?

A. 1;

B. 2;

C. 3;

D. 0.

Hướng dẫn giải:

Đáp án đúng là: A.

(1) Ta có:

P: “Một số tự nhiên n chia hết cho 24”.

Q: “n chia hết cho 4 và 6”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một số tự nhiên n chia hết cho 4 và 6 thì nó chia hết cho 24”.

Ta thấy mệnh đề trên sai vì một số tự nhiên chia hết cho 4 và 6 chưa chắc nó đã chia hết cho 24.

Ví dụ: Số 12 chia hết cho cả 4 và 6, tuy nhiên nó không chia hết cho 24.

(2) Ta có:

P: “Mỗi số tự nhiên a, b chia hết cho 11”.

Q: “Tổng hai số a và b chia hết cho 11”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu tổng hai số a và b chia hết cho 11 thì mỗi số tự nhiên a, b chia hết cho 11”.

Ta thấy mệnh đề trên sai vì tổng hai số a và b chia hết cho 11 thì mỗi số a và b chưa chắn đã chia hết cho 11.

Chẳng hạn a = 5, b = 6, a + b = 11.

Ta thấy tổng a + b = 11 chia hết cho 11, tuy nhiên 5 và 6 lại không chia hết cho 11.

(3) Ta có:

P: “Một tứ giác là hình thang cân”.

Q: “Hai đường chéo của nó bằng nhau”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu hai đường chéo của một tứ giác bằng nhau thì tứ giác đó là hình thang cân”.

Ta thấy mệnh đề trên đúng vì một tứ giác có hai đường chéo bằng nhau thì nó là hình thang cân (theo dấu hiệu nhận biết).

Vì vậy có một mệnh đề đảo đúng.

Bài 6. Cho mệnh đề: “Điều kiện cần và đủ để mỗi số nguyên a, b chia hết cho 7 là tổng bình phương của chúng chia hết cho 7”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?

A. “Điều kiện đủ để mỗi số nguyên a, b chia hết cho 7 là tổng bình phương của chúng chia hết cho 7”;

B. “Mỗi số nguyên a, b chia hết cho 7 khi và chỉ khi tổng bình phương của chúng chia hết cho 7”;

C. “Mỗi số nguyên a, b chia hết cho 7 kéo theo tổng bình phương của chúng chia hết cho 7”;

D. “Mỗi số nguyên a, b chia hết cho 7 là điều kiện cần để tổng bình phương của chúng chia hết cho 7”;

Hướng dẫn giải:

Đáp án đúng là: B.

Xét mệnh đề: “Điều kiện cần và đủ để mỗi số nguyên a, b chia hết cho 7 là tổng bình phương của chúng chia hết cho 7”.

Đặt:

P: “Mỗi số nguyên a, b chia hết cho 7”.

Q: “Tổng bình phương của chúng chia hết cho 7”.

Ta viết lại các mệnh đề ở đáp án như sau:

A. Điều kiện đủ để có P là Q.

B. P khi và chỉ khi Q.

C. P kéo theo Q.

D. P là điều kiện cần để có Q.

Đối với mệnh đề P ⇔ Q, ta có thể phát biểu theo một số cách sau:

+ P tương đương Q;

+ P là điều kiện cần và đủ để có Q;

+ P nếu và chỉ nếu Q;

+ P khi và chỉ khi Q.

Ta thấy chỉ có cách phát biểu ở câu B tương đương với mệnh đề đã cho nên mệnh đề ở câu B là cách viết đúng.

Bài 7. Mệnh đề nào dưới đây đúng?

A. “Tổng a + b là số chẵn khi và chỉ khi a, b đều là số chẵn”;

B. “Tích a.b là số chẵn khi và chỉ khi a, b đều là số chẵn”;

C. “Hai số a, b chia hết cho c khi và chỉ khi a + b chia hết cho c”;

D. “Tam giác ABC đều khi và chỉ khi AB = AC = BC”.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Ta có:

P: “Tổng a + b là số chẵn”.

Q: “a, b đều là số chẵn”.

- Xét mệnh đề P ⇒ Q: “Nếu tổng a + b là số chẵn thì a, b đều là số chẵn”.

Ta thấy mệnh đề này sai do nếu tổng hai số là một số chẵn thì hai số đó không cần thiết phải đều chẵn. (1)

Chẳng hạn:

a + b = 6 thì  a, b có thể nhận giá trị là a = 1, b = 5 đều là số lẻ.

- Xét mệnh đề đảo Q ⇒ P: “Nếu a, b đều là số chẵn thì tổng a + b là số chẵn”.

Ta thấy mệnh đề này đúng. (2)

Ví dụ:

a = 2, b = 6 đều là số chẵn và tổng a + b = 2 + 6 = 8 là số chẵn.

Từ (1) và (2) suy ra mệnh đề đã cho sai.

B. Ta có:

P: “Tích a.b là số chẵn”.

Q: “a, b đều là số chẵn”.

- Xét mệnh đề P ⇒ Q: “Nếu tích a.b là số chẵn thì a, b đều là số chẵn”.

Ta thấy mệnh đề này sai do nếu tích hai số là một số chẵn thì hai số đó không cần thiết phải đều chẵn. (3)

Chẳng hạn:

a.b = 6 thì  a, b có thể nhận giá trị là a = 2, b = 3 là một số chẵn và một số lẻ.

- Xét mệnh đề đảo Q ⇒ P: “Nếu a, b đều là số chẵn thì tích a.b là số chẵn”.

Ta thấy mệnh đề này đúng. (4)

Ví dụ:

a = 2, b = 4 đều là số chẵn và tổng a.b = 2.4 = 8 là số chẵn.

Từ (3) và (4) suy ra mệnh đề đã cho sai.

C. Ta có:

P: “Hai số a, b chia hết cho c”.

Q: “a + b chia hết cho c”.

- Xét mệnh đề P ⇒ Q: “Nếu hai số a, b chia hết cho c thì a + b chia hết cho c”.

Ta thấy mệnh đề này đúng do nếu hai số đều chia hết cho một số thứ 3 thì tổng của hai số đó cũng chia hết cho số thứ 3. (5)

Chẳng hạn:

6 chia hết cho 2; 8 chia hết cho 2 thì 6 + 8 = 14 cũng chia hết cho 2.

- Xét mệnh đề đảo Q ⇒ P: “Nếu a + b chia hết cho c thì hai số a, b đều chia hết cho c”.

Ta thấy mệnh đề này sai do nếu tổng hai số chia hết cho một số thứ ba thì hai số chưa chắc đã chia hết cho số thứ 3. (6)

Ví dụ:

a = 3, b = 6.

⇒ a + b = 3 + 6 = 9 chia hết cho 9, tuy nhiên hai số a và b lại không chia hết cho 9.

Từ (5) và (6) suy ra mệnh đề đã cho sai.

D. Ta có:

P: “Tam giác ABC đều”.

Q: “AB = BC = AC”.

- Xét mệnh đề P ⇒ Q: “Nếu tam giác ABC đều thì AB = BC = AC”.

Ta thấy mệnh đề này đúng vì một tam giác là tam giác đều thì tam giác đó sẽ có ba cạnh bằng nhau. (7)

- Xét mệnh đề đảo Q ⇒ P: “Nếu AB = BC = AC thì tam giác ABC đều”.

Ta thấy mệnh đề này đúng vì một tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều. (8)

Từ (7) và (8) suy ra mệnh đề đã cho đúng.

Bài 8. Cho mệnh đề: “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”.

Mệnh đề đảo của mệnh đề trên là:

A. “Tứ giác là một hình thoi khi và chỉ khi tứ giác đó nội tiếp được trong một đường tròn”;

B. “Một tứ giác nội tiếp được trong một đường tròn khi và chỉ khi tứ giác đó là hình thoi”;

C. “Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”;

D. “Tứ giác là một hình thoi kéo theo tứ giác đó nội tiếp được trong một đường tròn”.

Hướng dẫn giải:

Đáp án đúng là: C.

Xét mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được trong một đường tròn”, ta có:

P: “Tứ giác là một hình thoi”.

Q: “Tứ giác đó nội tiếp được một đường tròn”.

Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”

Đối chiếu với các đáp án, ta thấy mệnh đề ở câu C là phù hợp nhất.

Bài 9. Cho tứ giác ABCD, ta có các mệnh đề sau:

P: “ABCD là hình vuông”.

Q: “ABCD là hình chữ nhật”.

Mệnh đề nào sau đây đúng?

A. P ⇒ Q;

B. Q ⇒ P;

C. P ⇒ $\overline{\mathrm{Q}}$;

D. $\overline{\mathrm{P}}$ ⇒ Q.

Hướng dẫn giải:

Đáp án đúng là: A.

A. Mệnh đề P ⇒ Q được phát biểu như sau:

“Nếu ABCD là hình vuông thì ABCD là hình chữ nhật”.

Mệnh đề trên đúng vì một tứ giác là hình vuông thì nó cũng là hình chữ nhật.

B. Mệnh đề Q ⇒ P được phát biểu như sau:

“Nếu ABCD là hình chữ nhật thì ABCD là hình vuông”.

Mệnh đề này sai do hình chữ nhật có hai cặp cạnh đối bằng nhau, còn hình vuông thì bốn cạnh phải bằng nhau, nên một tứ giác là hình chữ nhật thì nó chưa chắc đã là hình vuông.

C. Ta có mệnh đề $\overline{\mathrm{Q}}$: “ABCD không phải là hình chữ nhật”.

Mệnh đề P ⇒ $\overline{\mathrm{Q}}$ được phát biểu như sau:

“Nếu ABCD là hình vuông thì ABCD không phải là hình chữ nhật”.

Mệnh đề này sai vì một tứ giác là hình vuông thì nó cũng là hình chữ nhật.

D. Ta có mệnh đề $\overline{\mathrm{P}}$: “ABCD không phải là hình vuông”.

Mệnh đề $\overline{\mathrm{P}}$ ⇒ Q được phát biểu như sau:

“Nếu ABCD không phải là hình vuông thì ABCD là hình chữ nhật”.

Ta thấy mệnh đề trên sai do một tứ giác không phải là hình vuông thì nó có thể là hình khác chứ không nhất thiết là hình chữ nhật.

Bài 10. Cho mệnh đề sau:

Cho tứ giác ABCD, ta có các mệnh đề sau:

P: “x là số nguyên dương”.

Q: “x² là số nguyên dương”.

Mệnh đề nào sau đây đúng?

A. P ⇔ Q;

B. Q ⇒ P;

C. P ⇒ $\overline{\mathrm{Q}}$;

D. P ⇒ Q.

Hướng dẫn giải:

Đáp án đúng là: D.

A. Xét mệnh đề P ⇒ Q: “Nếu x là số nguyên dương thì x² là số nguyên dương”.

Mệnh đề này đúng vì bình phương của một số nguyên dương là một số nguyên dương. (1)

Xét mệnh đề đảo Q ⇒ P: “Nếu x² là số nguyên dương thì x là số nguyên dương”.

Mệnh đề này sai do nếu x² là số nguyên dương thì x có thể là số nguyên dương hoặc số nguyên âm. (2)

Từ (1) và (2) nên mệnh đề ở cây A sai.

B. Mệnh đề Q ⇒ P được phát biểu như sau: “Nếu x² là số nguyên dương thì x là số nguyên dương”.

Mệnh đề này sai do nếu x² là số nguyên dương thì x có thể là số nguyên dương hoặc số nguyên âm.

C. Ta có mệnh đề $\overline{\mathrm{Q}}$: “x² không phải là số nguyên dương”.

Mệnh đề P ⇒ $\overline{\mathrm{Q}}$ được phát biểu như sau: “Nếu x là số nguyên dương thì x² không phải là số nguyên dương”.

Vì x² luôn luôn dương nên mệnh đề trên sai.

D. Mệnh đề P ⇒ Q được phát biểu như sau: “Nếu x là số nguyên dương thì x² là số nguyên dương”.

Mệnh đề này đúng vì bình phương của một số nguyên dương là một số nguyên dương.

Bài 11. Trong các mệnh đề sau, mệnh đề nào có phát biểu là định lý?

A. Nếu một tứ giác là hình chữ nhật thì tứ giác đó có bốn cạnh bằng nhau;

B. Nếu một số tự nhiên tận cùng là 5 thì số đó chia hết cho 5;

C. Nếu một tự nhiên chia hết cho 3 thì nó chia hết cho 9;

D. Nếu một tứ giác có hai đường chéo vuông góc với nhau thì tứ giác đó là hình thoi.

Hướng dẫn giải:

Đáp án đúng là: B.

A. Vì hình chữ nhật có hai cặp cạnh đối bằng nhau nên mệnh đề ở câu A sai.

Do đó mệnh đề trên không phải là định lý.

B. Mệnh đề ở câu B đúng do dấu hiệu để một số chia hết cho 5 là số đó có chữ số tận cùng là 0 hoặc 5.

Vì vậy mệnh đề câu B là định lý.

C. Ta có một số chia hết cho 9 thì nó cũng chia hết cho 3, tuy nhiên một số chia hết cho 3 thì nó chưa chắc chia hết cho 9.

Chẳng hạn số 3 chia hết cho 3 nhưng nó không chia hết cho 9.

Nên mệnh đề ở câu C sai và nó không phải là định lý.

D. Mệnh đề ở câu D sai do một tứ giác có hai đường chéo vuông góc với nhau thì chưa chắc nó đã là hình thoi.

Vì vậy mệnh đề trên không phải là định lý.

Bài 12. Cho định lý sau: “Nếu hai tam giác bằng nhau thì hai tam giác đó đồng dạng”.

Phát biểu định lý trên dưới dạng điều kiện cần.

A. Hai tam giác bằng nhau kéo theo hai tam giác đó đồng dạng;

B. Hai tam giác bằng nhau là điều kiện cần để hai tam giác đó đồng dạng;

C. Hai tam giác đồng dạng là điều kiện cần để hai tam giác đó bằng nhau;

D. Hai tam giác bằng nhau tương đương với hai tam giác đó đồng dạng.

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

P: “Hai tam giác bằng nhau”.

Q: “Hai tam giác đó đồng dạng”.

Ta thấy định lý trên có dạng P ⇒ Q có thể được phát biểu dưới dạng điều kiện cần như sau:

Q là điều kiện cần để có P.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện cần là:

Hai tam giác đồng dạng là điều kiện cần để hai tam giác đó bằng nhau.

Bài 13. Cho định lý sau: “Nếu một số tự nhiên chỉ chia hết cho 1 và chính nó thì số đó là số nguyên tố”.

Phát biểu định lý trên dưới dạng điều kiện đủ.

A. Một số tự nhiên chỉ chia hết cho 1 và chính nó khi và chỉ khi số đó là số nguyên tố;

B. Một số tự nhiên chỉ chia hết cho 1 và chính nó là điều kiện đủ để số đó là số nguyên tố;

C. Một số tự nhiên là số nguyên tố là điều kiện đủ để số đó chia hết cho 1 và chính nó;

D. Điều kiện cần và đủ để một số tự nhiên chỉ chia hết cho 1 và chính nó là số đó là số nguyên tố.

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có:

P: “ Nếu một số tự nhiên chỉ chia hết cho 1 và chính nó”.

Q: “Số đó là số nguyên tố”.

Ta thấy định lý trên có dạng P ⇒ Q có thể được phát biểu dưới dạng điều kiện đủ như sau:

P là điều kiện đủ để có Q.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện đủ là:

Một số tự nhiên chỉ chia hết cho 1 và chính nó là điều kiện đủ để số đó là số nguyên tố.

Bài 14. Cho các mệnh đề sau:

(1) Nếu tích của hai số a và b lớn hơn 0 thì a và b đều dương.

(2) Nếu a, b là hai số nguyên dương thì tích của chúng cũng là một số nguyên dương.

(3) Nếu tích của hai số a và b là một số nguyên âm thì trong hai số đó phải có một số nguyên dương và một số nguyên âm.

Trong các mệnh đề trên, có bao nhiêu mệnh đề là định lý?

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải:

Đáp án đúng là: C.

(1) Ta có ví dụ sau :

a = – 2, b = – 4

a.b = (– 2).(– 4) = 8

Từ ví dụ trên ta thấy mặc dù tích của a và b là một số dương nhưng a và b đều là các số âm.

Do đó mệnh đề (1) sai và không phải là định lý.

(2) Ta có ví dụ sau:

Tích của hai số nguyên dương là một số nguyên dương là mệnh đề đúng (tích của hai số nguyên cùng dấu là số nguyên dương).

Do đó mệnh đề (2) là định lý.

(3) Ta có ví dụ sau :

Tích của hai số nguyên khác dấu thì là số nguyên âm.

Do đó mệnh đề (3) là định lý.

Vậy có hai mệnh đề là định lý.

Bài 15. Cho định lý sau: “Một tam giác là tam giác đều thì tam giác đó có ba đường phân giác bằng nhau”.

Phát biểu định lý đảo của định lý trên dưới dạng điều kiện cần.

A. Một tam giác là tam giác đều là điều kiện cần để tam giác đó có ba đường phân giác bằng nhau;

B. Một tam giác có ba đường phân giác bằng nhau là điều kiện cần để tam giác đó là tam giác đều;

C. Một tam giác là tam giác đều khi và chỉ khi tam giác đó có ba đường phân giác bằng nhau;

D. Một tam giác là tam giác đều là điều kiện cần và đủ để tam giác đó có ba đường phân giác bằng nhau.

Hướng dẫn giải:

Đáp án đúng là: A.

Xét mệnh đề “Một tam giác là tam giác đều thì tam giác đó có ba đường phân giác bằng nhau” ta có:

P: “Một tam giác là tam giác đều”

Q: “Tam giác đó có ba đường phân giác bằng nhau”

Định lý đảo Q ⇒ P của định lý trên được phát biểu như sau:

“Một tam giác có ba đường phân giác bằng nhau thì tam giác đó là tam giác đều”.

Xét định lý đảo trên ta có :

A: “Một tam giác có ba đường phân giác bằng nhau”.

B: “Tam giác đó là tam giác đều”.

Ta thấy định lý trên có dạng A ⇒ B có thể được phát biểu dưới dạng điều kiện cần như sau:

B là điều kiện cần để có A.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện cần là:

“Một tam giác là tam giác đều là điều kiện cần để tam giác đó có ba đường phân giác bằng nhau”.

Bài 16. Cho định lý sau: “Nếu mỗi số nguyên a, b chia hết cho 7 thì tổng các bình phương của chúng chia hết cho 7”.

Phát biểu định lý đảo của định lý trên dưới dạng điều kiện đủ.

A. Mỗi số nguyên a, b chia hết cho 7 tương đương với tổng các bình phương của chúng chia hết cho 7;

B. Mỗi số nguyên a, b chia hết cho 7 là điều kiện đủ để tổng các bình phương của chúng chia hết cho 7;

C. Tổng bình phương của hai số nguyên a, b chia hết cho 7 là điều kiện đủ để mỗi số nguyên đó chia hết cho 7;

D. Mỗi số nguyên a, b chia hết cho 7 kéo theo tổng các bình phương của chúng chia hết cho 7.

Hướng dẫn giải:

Đáp án đúng là: C.

Xét mệnh đề “Nếu mỗi số nguyên a, b chia hết cho 7 thì tổng các bình phương của chúng chia hết cho 7” ta có:

P: “Mỗi số nguyên a, b chia hết cho 7”

Q: “Tổng bình phương của chúng chia hết cho 7”

Định lý đảo Q ⇒ P của định lý trên được phát biểu như sau:

“Nếu tổng bình phương của hai số a và b chia hết cho 7 thì mỗi số nguyên đó chi hết cho 7”.

Xét định lý đảo trên ta có :

A: “Tổng bình phương của hai số a và b chia hết cho 7”.

B: “Mỗi số nguyên đó chi hết cho 7”.

Ta thấy định lý trên có dạng A ⇒ B có thể được phát biểu dưới dạng điều kiện đủ như sau:

A là điều kiện đủ để có B.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện đủ là:

“Tổng bình phương của hai số nguyên a, b chia hết cho 7 là điều kiện đủ để mỗi số nguyên đó chia hết cho 7”.

Bài 17. Cho mệnh đề sau: “Nếu x là một số nguyên tố lớn hơn 3 thì x² + 20 là một hợp số (tức là số có ước khác 1 và chính nó)”.

Đáp án nào dưới đây là cách viết khác với mệnh đề đã cho?

A. Điều kiện cần để x² + 20 là một hợp số là x là số nguyên tố lớn hơn 3;

B. Điều kiện đủ để x² + 20 là một hợp số là x là số nguyên tố lớn hơn 3;

C. Điều kiện cần và đủ để x² + 20 là một hợp số là x là số nguyên tố lớn hơn 3;

D. Cả A và B đều đúng.

Hướng dẫn giải:

Đáp án đúng là: B.

Xét mệnh đề “Nếu x là một số nguyên tố lớn hơn 3 thì x² + 20 là một hợp số” ta có:

P: “x là một số nguyên tố lớn hơn 3”.

Q: “x² + 20 là một hợp số”.

Ta thấy mệnh đề trên có dạng P ⇒ Q có thể được phát biểu dưới dạng điều kiện cần, điều kiện đủ như sau:

+ Điều kiện cần để có P là Q.

+ Điều kiện đủ để có Q là P.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện cần, điều kiện đủ lần lượt là:

+ Điều kiện cần để x là một số nguyên tố lớn hơn 3 là x² + 20 là một hợp số.

+ Điều kiện đủ để x² + 20 là một hợp số là x là một số nguyên tố lớn hơn 3.

Đối chiếu với các đáp án trên, ta thấy mệnh đề ở đáp án B là một cách viết khác của mệnh đề đã cho.

Bài 18. Cho mệnh đề sau: “Trong một mặt phẳng, nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau”.

Đáp án nào dưới đây là cách viết khác với mệnh đề đã cho?

A. Trong một mặt phẳng, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 là điều kiện cần để hai đường thẳng đó song song với nhau;

B. Trong một mặt phẳng, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 tương đương với để hai đường thẳng đó song song với nhau;

C. Trong một mặt phẳng, hai đường thẳng phân biệt song song với nhau là điều kiện đủ để hai đường thẳng đó cùng song song với đường thẳng thứ 3;

D. Trong một mặt phẳng, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 là điều kiện đủ để hai đường thẳng đó song song với nhau.

Hướng dẫn giải:

Đáp án đúng là: D.

Xét mệnh đề “Trong một mặt phẳng, nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì hai đường thẳng đó song song với nhau” ta có:

P: “Trong một mặt phẳng, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3”.

Q: “Hai đường thẳng đó song song với nhau”.

Ta thấy mệnh đề trên có dạng P ⇒ Q có thể được phát biểu dưới dạng điều kiện cần, điều kiện đủ như sau:

+ P là điều kiện đủ để có Q.

+ Q là điều kiện cần để có P.

Do đó định lý đã cho được phát biểu dưới dạng điều kiện cần, điều kiện đủ lần lượt là:

+ Trong một mặt phẳng, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 là điều kiện đủ để hai đường thẳng đó song song với nhau.

+ Trong một mặt phẳng, hai đường thẳng phân biệt song song với nhau là điều kiện cần để hai đường thẳng đó cùng song song với đường thẳng thứ 3.

Đối chiếu với các đáp án trên, ta thấy mệnh đề ở đáp án D là một cách viết khác của mệnh đề đã cho.

Bài 19. Cho định lý sau: “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.

Cho biết giả thiết, kết luận của định lý trên.

A. “Hai tam giác bằng nhau” và “diện tích của chúng bằng nhau” đều là giả thiết của định lý;

B. “Hai tam giác bằng nhau” và “diện tích của chúng bằng nhau” đều là kết luận của định lý;

C. “Hai tam giác bằng nhau” là giả thiết, “diện tích của chúng bằng nhau” là kết luận của định lý;

D. “Hai tam giác bằng nhau” là kết luận, “diện tích của chúng bằng nhau” là giả thiết của định lý.

Hướng dẫn giải:

Đáp án đúng là: C.

Theo lý thuyết, cho định lý P ⇒ Q.

Khi đó P là giả thiết, Q là kết luận.

Ta có:

P: “Hai tam giác bằng nhau”.

Q: “Diện tích của chúng bằng nhau”.

Do đó “Hai tam giác bằng nhau” là giả thiết, “Diện tích của chúng bằng nhau” là kết luận của định lý.

Bài 20. Cho định lý sau: “Nếu tam giác có hai góc bằng 45° thì tam giác đó là tam giác vuông cân”.

Cho biết giả thiết, kết luận của định lý trên.

A. “Tam giác có hai góc bằng 45°” là giả thiết, “tam giác đó là tam giác vuông cân” là kết luận của định lý;

B. “Tam giác có hai góc bằng 45°” và “tam giác đó là tam giác vuông cân” đều là kết luận của định lý;

C. “Tam giác có hai góc bằng 45°” và “tam giác đó là tam giác vuông cân” đều là giả thiết của định lý;

D. “Tam giác có hai góc bằng 45°” là kết luận, “tam giác đó là tam giác vuông cân” là giả thiết của định lý.

Hướng dẫn giải:

Đáp án đúng là: A.

Theo lý thuyết, cho định lý P ⇒ Q.

Khi đó P là giả thiết, Q là kết luận.

Ta có:

P: “Tam giác có hai góc bằng 45°”.

Q: “Tam giác đó là tam giác vuông cân”.

Do đó “Tam giác có hai góc bằng 45°” là giả thiết, “Tam giác đó là tam giác vuông cân” là kết luận của định lý.

Xem thêm các dạng bài tập hay khác:

90 Bài tập các khái niệm mở đầu (có đáp án )

80 Bài tập về Tập hợp và các phép toán trên tập hợp (có đáp án )

100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2024)

200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2024)

500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2024)