Lý thuyết Toán 11 Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song (Cánh diều)

Lý thuyết Toán 11 Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

1. Đường thẳng và mặt phẳng trong không gian

1.1. Khái niệm mở đầu

a) Mặt phẳng

Nhận xét: Mặt sân vận động cho ta hình ảnh một phần của mặt phẳng trong không gian.

Người ta thường biểu diễn một mặt phẳng bằng một hình bình hành và dùng các chữ cái đặt trong dấu ngoặc đơn ( ) để đặt tên cho mặt phẳng ấy.

Ví dụ: Mặt phẳng (P) (Hình 1), mặt phẳng (Q), mặt phẳng (α), mặt phẳng (β),...

b) Điểm thuộc mặt phẳng

Với mỗi điểm A và mặt phẳng (P), chỉ xảy ra một trong hai khả năng sau:

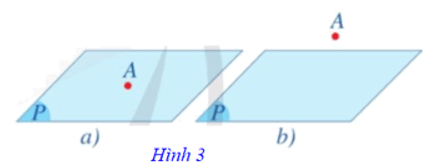
⦁ Điểm A thuộc mặt phẳng (P), ta kí hiệu A ∈ (P) (Hình 3a). Ta còn nói “điểm A nằm trong (hay nằm trên) mặt phẳng (P)”; “mặt phẳng (P) đi qua điểm A”;

⦁ Điểm A không thuộc mặt phẳng (P) hay A nằm ngoài (P), ta kí hiệu A ∉ (P) (Hình 3b).

c) Hình biểu diễn của một hình trong không gian

* Khái niệm

Quy ước: Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian gọi là hình biểu diễn của hình không gian đó.

* Quy tắc vẽ hình biểu diễn của một hình trong không gian

Để việc vẽ hình biểu diễn của một hình trong không gian được thuận lợi và thống nhất, ta quy ước như sau:

(1) Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng được biểu diễn bởi đoạn thẳng;

(2) Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau);

(3) Hình biểu diễn giữ nguyên tính liên thuộc giữa điểm với đường thẳng hoặc với đoạn thẳng;

(4) Những đường nhìn thấy được vẽ bằng nét liền, những đường không nhìn thấy được vẽ bằng nét đứt.

Chú ý: Các quy tắc khác sẽ được đề cập sau.

1.2. Các tính chất thừa nhận của hình học không gian

Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

Tức là, có duy nhất một đường thẳng d đi qua hai điểm A, B phân biệt.

Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

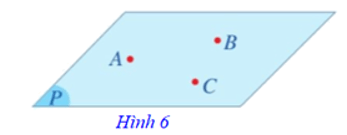
Như vậy, mặt phẳng hoàn toàn xác định khi biết ba điểm A, B, C không thẳng hàng. Mặt phẳng đó được kí hiệu là mp(ABC) hay đơn giản là (ABC) (Hình 6).

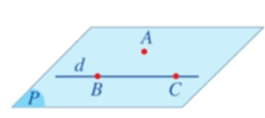
Tính chất 3: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.

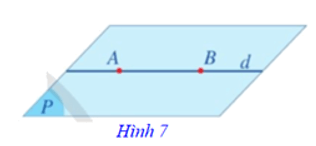
Như vậy, nếu một đường thẳng d đi qua hai điểm phân biệt A, B của mặt phẳng (P) thì mọi điểm của đường thẳng d đều nằm trong mặt phẳng (P). Khi đó, ta nói d nằm trong (P), hoặc (P) chứa d, hoặc (P) đi qua d, kí hiệu d ⊂ (P) hay (P) ⊃ d (Hình 7).

Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

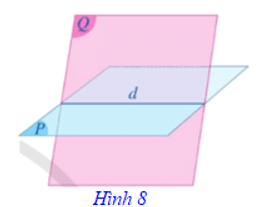
Nếu hai mặt phẳng phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu d = (P) ∩ (Q) (Hình 8).

Nhận xét:

⦁ Có thể xác định giao tuyến của hai mặt phẳng bằng cách đi tìm hai điểm chung của chúng. Đường thẳng đi qua hai điểm chung đó là giao tuyến cần tìm.

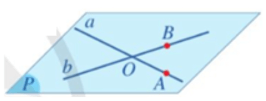
⦁ Để tìm giao điểm của đường thẳng a và mặt phẳng (P) (với giả thiết a cắt (P)), ta có thể làm như sau: Chọn một đường thẳng b thích hợp trong mặt phẳng (P) và tìm giao điểm M của hai đường thẳng a và b. Khi đó, M là giao điểm cần tìm.

Tính chất 6: Trên mỗi mặt phẳng của không gian, các kết quả đã biết của hình học phẳng đều đúng.

1.3. Một số cách xác định mặt phẳng

Định lí 1: Cho điểm A không thuộc đường thẳng d. Khi đó, qua điểm A và đường thẳng d có một và chỉ một mặt phẳng, kí hiệu mp(A, d) hoặc (A, d).

Định lí 2: Cho hai đường thẳng a và b cắt nhau. Khi đó, qua a và b có một và chỉ một mặt phẳng, kí hiệu mp(a, b).

Nhận xét: Từ Tính chất 2 và hai định lí trên, ta thấy mặt phẳng hoàn toàn được xác định theo một trong ba cách sau:

⦁ Đi qua ba điểm không thẳng hàng;

⦁ Đi qua một đường thẳng và một điểm nằm ngoài đường thẳng đó;

⦁ Đi qua hai đường thẳng cắt nhau.

1.4. Hình chóp và hình tứ diện

a) Hình chóp

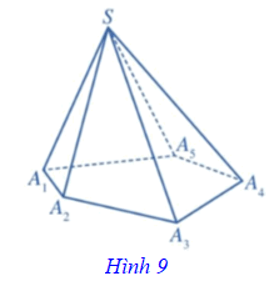
Trong mặt phẳng (P), cho đa giác A₁A₂...A_n (n ≥ 3). Lấy điểm S nằm ngoài (P). Nối S với các đỉnh A₁, A₂, ..., A_n ta được n tam giác: SA₁A₂, SA₂A₃, ..., SA_nA₁. Hình gồm đa giác A₁A₂...A_n và n tam giác SA₁A₂, SA₂A₃, ..., SA_nA₁ gọi là hình chóp, kí hiệu S.A₁A₂...A_n.

⦁ Trong hình chóp S.A₁A₂...A_n, ta có:

– Điểm S gọi là đỉnh;

– Đa giác A₁A₂...A_n gọi là mặt đáy;

– Các cạnh của mặt đáy gọi là cạnh đáy;

– Các đoạn thẳng SA₁, SA₂, ..., SA_n gọi là các cạnh bên;

– Các tam giác SA₁A₂, SA₂A₃, ..., SA_nA₁ gọi là các mặt bên.

⦁ Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,... thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,... Hình 9 minh họa cho hình chóp ngũ giác S.A₁A₂A₃A₄A₅.

b) Hình tứ diện

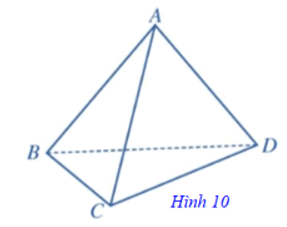
Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD gọi là hình tứ diện (hay ngắn gọn là tứ diện), kí hiệu là ABCD.

⦁ Trong hình tứ diện ABCD (Hình 10), ta có:

– Các điểm A, B, C, D gọi là các đỉnh.

– Các đoạn thẳng AB, BC, CD, DA, CA, BD gọi là các cạnh. Hai cạnh không có điểm chung gọi là hai cạnh đối diện.

– Các tam giác ABC, ACD, ABD, BCD gọi là các mặt.

– Đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.

⦁ Hình tứ diện có các mặt là tam giác đều gọi là hình tứ diện đều.

⦁ Mỗi hình chóp tam giác là một hình tứ diện. Ngược lại, nếu ta quy định rõ đỉnh và mặt đáy trong một hình tứ diện thì hình tứ diện đó trở thành hình chóp tam giác.

Nhận xét: Để chứng minh ba điểm thẳng hàng, ta có thể chỉ ra ba điểm đó cùng thuộc hai mặt phẳng phân biệt.

2. Hai đường thẳng song song trong không gian

2.1. Vị trí tương đối của hai đường thẳng phân biệt

Trong mục này, nếu không nói gì thêm, ta luôn giả sử hai đường thẳng là phân biệt.

Cho hai đường thẳng a và b phân biệt trong không gian. Khi đó chỉ xảy ra một trong các trường hợp sau:

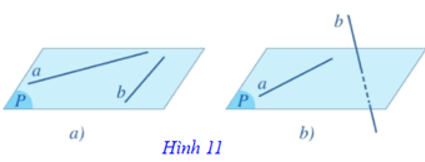
Trường hợp 1: Có một mặt phẳng chứa a và b. Khi đó ta nói a và b đồng phẳng (Hình 11a).

Trường hợp 2: Không có mặt phẳng nào chứa a và b. Khi đó ta nói a và b chéo nhau, hay a chéo với b (Hình 11b).

Khi hai đường thẳng a và b (phân biệt) đồng phẳng, có hai khả năng xảy ra:

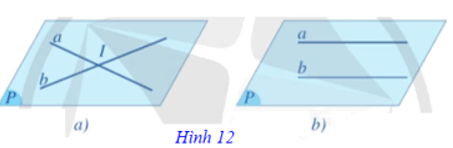
⦁ a và b có một điểm chung duy nhất I. Ta nói a và b cắt nhau tại I và kí hiệu là a ∩ b = {I}. Ta còn có thể viết a ∩ b = I (Hình 12a).

⦁ a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b (Hình 12b).

Khái niệm hai đường thẳng song song: Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.

Lưu ý: Cho hai đường thẳng song song a và b. Có duy nhất một mặt phẳng chứa hai đường thẳng đó, kí hiệu là mp(a, b).

2.2. Tính chất

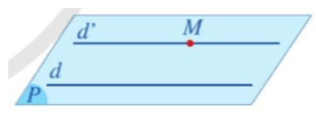
Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

Tức là, trong không gian, cho điểm M và đường thẳng d không đi qua M. Có một và chỉ một đường thẳng d’ đi qua điểm M và song song với đường thẳng d.

Định lí 2: (về giao tuyến của ba mặt phẳng)

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau.

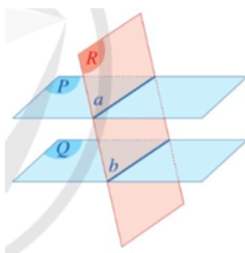
Tức là, trong không gian, cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a = (P) ∩ (R), b = (R) ∩ (Q), c = (Q) ∩ (P).

Khi đó ta có hai khả năng xảy ra như sau:

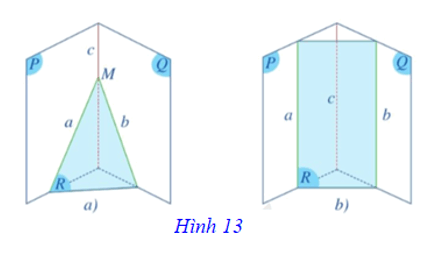
Trường hợp 1: Ba giao tuyến a, b, c đồng quy tại M (Hình 13a).

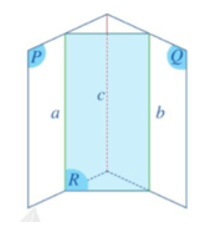
Trường hợp 2: Ba giao tuyến a, b, c song song với nhau (Hình 13b).

Từ Định lí 2, ta suy ra hệ quả sau:

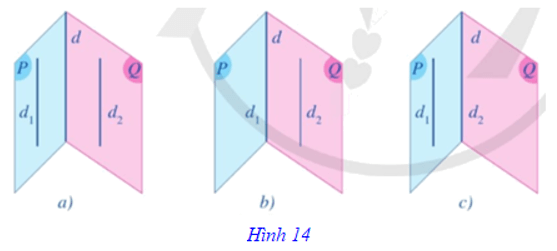
Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó (Hình 14).

Định lí 3: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

Khi hai đường thẳng a và b cùng song song với đường thẳng c, ta kí hiệu a // b // c và gọi là ba đường thẳng song song.

3. Đường thẳng và mặt phẳng song song

3.1. Đường thẳng song song với mặt phẳng

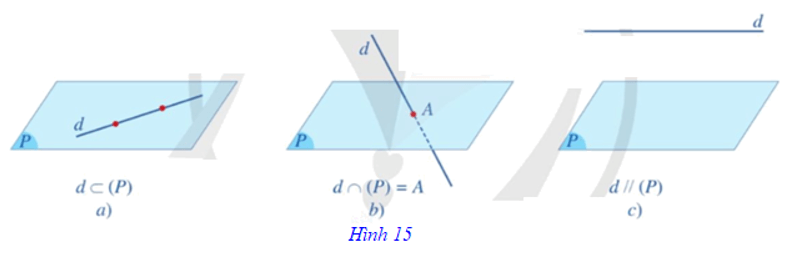
Có ba khả năng xảy ra đối với số điểm chung của d và (P) (Hình 15) là:

⦁ d và (P) có từ hai điểm chung trở lên. Khi đó đường thẳng d nằm trong mặt phẳng (P) hay (P) chứa d và kí hiệu là d ⊂ (P) hay (P) ⊃ d (Hình 15a).

⦁ d và (P) có một điểm chung duy nhất A. Khi đó ta nói d và (P) cắt nhau tại điểm A và kí hiệu là d ∩ (P) = {A} hay d ∩ (P) = A (Hình 15b).

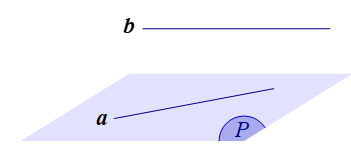
⦁ d và (P) không có điểm chung. Khi đó ta nói d song song với (P) hay (P) song song với d và kí hiệu là d // (P) hay (P) // d (Hình 15c).

Đường thẳng song song với mặt phẳng: Đường thẳng được gọi là song song với mặt phẳng nếu chúng không có điểm chung.

3.2. Điều kiện và tính chất

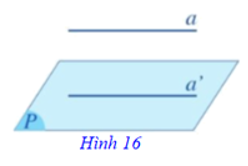
Định lí 1: (Dấu hiệu nhận biết một đường thẳng song song với một mặt phẳng (Hình 16)

Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P).

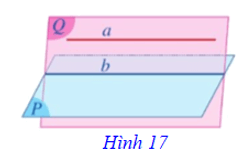
Định lí 2: (Tính chất của đường thẳng song song với mặt phẳng) (Hình 17)

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.

Hệ quả của Định lí 2:

Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Tức là, nếu hai mặt phẳng (P) và (Q) phân biệt cùng song song với đường thẳng a thì giao tuyến b của chúng (nếu có) cũng song song với đường thẳng a.

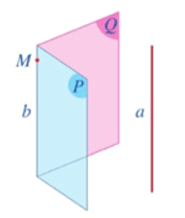
Chú ý: Cho hai đường thẳng chéo nhau. Khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Tức là, cho hai đường thẳng a và b chéo nhau. Khi đó có duy nhất một mặt phẳng (P) chứa đường thẳng a và song song với đường thẳng b.

4. Hai mặt phẳng song song

4.1. Hai mặt phẳng song song

Đối với hai mặt phẳng phân biệt (P) và (Q) trong không gian, có hai khả năng xảy ra:

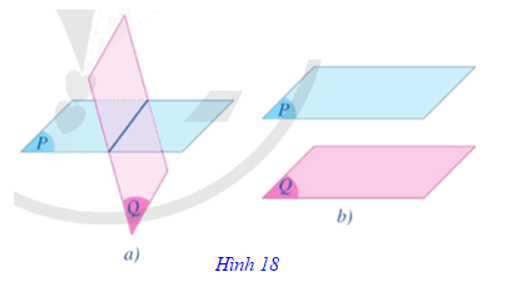
⦁ Hai mặt phẳng (P) và (Q) có điểm chung. Khi đó, chúng cắt nhau theo một đường thẳng (Hình 18a).

⦁ Hai mặt phẳng (P) và (Q) không có điểm chung. Khi đó, ta nói chúng song song với nhau, kí hiệu (P) // (Q) hay (Q) // (P) (Hình 18b).

Hai mặt phẳng song song: Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.

4.2. Điều kiện và tính chất

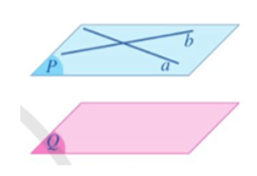
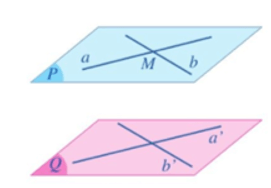
Định lí 1: (Dấu hiệu nhận biết hai mặt phẳng song song)

Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

Định lí 2: (Tính chất về hai mặt phẳng song song)

Qua một điểm nằm ngoài một mặt phẳng cho trước, có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

Tức là, cho điểm M nằm ngoài mặt phẳng (Q), có duy nhất một mặt phẳng (P) chứa điểm M và song song với mặt phẳng (Q).

Từ định lí trên, ta có các hệ quả sau:

Hệ quả 1. Nếu đường thẳng a song song với mặt phẳng (Q) thì có duy nhất một mặt phẳng (P) chứa a và song song với mặt phẳng (Q).

Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

Định lí 3: Cho hai mặt phẳng song song (P) và (Q). Nếu mặt phẳng (R) cắt mặt phẳng (P) thì cũng cắt mặt phẳng (Q) và hai giao tuyến a, b của chúng song song với nhau.

4.3. Định lí Thalès

Định lí 4: (Định lí Thalès)

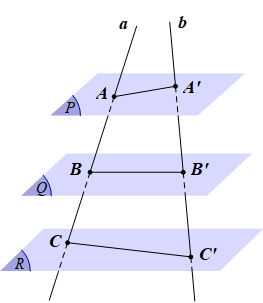
Nếu a, b là hai đường thẳng phân biệt cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì:

$\frac{AB}{A^{\text{'}}{B}^{\text{'}}}=\frac{BC}{B^{\text{'}}{C}^{\text{'}}}=\frac{CA}{C^{\text{'}}{A}^{\text{'}}}$.

5. Hình lăng trụ và hình hộp

5.1. Hình lăng trụ

a) Định nghĩa

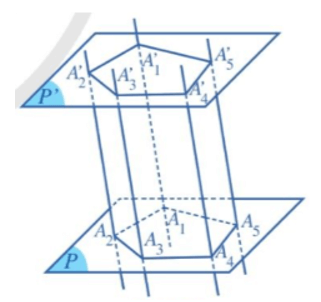
Hình gồm hai đa giác A₁A₂...A_n, A₁’A₂’...A_n’ và các hình bình hành A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, ..., A_nA₁A₁’A_n’ được gọi là hình lăng trụ, kí hiệu là A₁A₂...A_n.A₁’A₂’...A_n’.

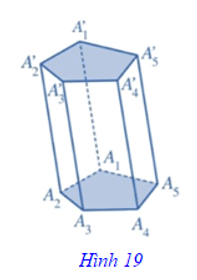
Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,... thì hình lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác (Hình 19),...

Trong hình lăng trụ A₁A₂...A_n.A₁’A₂’...A_n’:

– Hai đa giác A₁A₂...A_n và A₁’A₂’...A_n’ gọi là hai mặt đáy;

– Các hình bình hành A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, ..., A_nA₁A₁’A_n’ gọi là các mặt bên;

– Các cạnh của hai mặt đáy gọi là các cạnh đáy;

– Các đoạn thẳng A₁A₁’, A₂A₂’, ..., A_nA_n’ gọi là các cạnh bên;

– Các đỉnh của hai mặt đáy gọi là các đỉnh của hình lăng trụ.

b) Tính chất

Hình lăng trụ có:

⦁ Các cạnh bên song song và bằng nhau.

⦁ Các mặt bên là các hình bình hành.

⦁ Hai mặt đáy là hai đa giác có các cạnh tương ứng song song và bằng nhau.

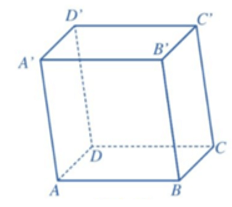
5.2. Hình hộp

a) Định nghĩa

Hình hộp là hình lăng trụ có đáy là hình bình hành.

Trong mỗi hình hộp, ta gọi:

– Hai mặt không có đỉnh chung là hai mặt đối diện;

– Hai cạnh song song không nằm trong một mặt là hai cạnh đối diện;

– Hai đỉnh không thuộc cùng một mặt là hai đỉnh đối diện;

– Đoạn thẳng nối hai đỉnh đối diện là đường chéo.

b) Tính chất

Hình hộp là một hình lăng trụ nên hình hộp có các tính chất của hình lăng trụ, ngoài ra:

⦁ Các mặt của hình hộp là các hình bình hành.

⦁ Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.

Nhận xét: Ta có thể coi hai mặt đối diện bất kì của một hình hộp là hai mặt đáy của nó.

6. Phép chiếu song song. Hình biểu diễn của một hình không gian

6.1. Phép chiếu song song

a) Định nghĩa

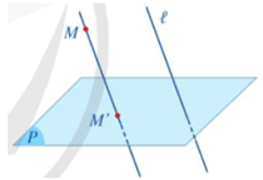
Cho mặt phẳng (P) và đường thẳng ℓ cắt mặt phẳng (P). Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng (P) sao cho MM’ song song hoặc trùng với ℓ gọi là phép chiếu song song lên mặt phẳng (P) theo phương của đường thẳng ℓ hoặc nói gọn là theo phương ℓ.

Mặt phẳng (P) gọi là mặt phẳng chiếu, phương ℓ gọi là phương chiếu, điểm M’ gọi là hình chiếu song song (hoặc ảnh) của điểm M qua phép chiếu song song nói trên.

Cho hình ℋ. Tập hợp ℋ ’ gồm hình chiếu song song của tất cả các điểm thuộc ℋ gọi là hình chiếu song song (hoặc ảnh) của hình ℋ qua phép chiếu song song nói trên.

b) Tính chất

Ta đã biết: Nếu một đường thẳng có phương trùng với phương chiếu thì hình chiếu của đường thẳng đó (hoặc một phần của nó) là một điểm.

Vì thế, trong các tính chất dưới đây, ta chỉ xét hình chiếu song song của các đường thẳng (hoặc một phần của chúng) khi các đường thẳng đó có phương không trùng với phương chiếu.

Định lí:

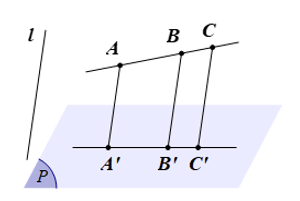
⦁ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

⦁ Phép chiếu song song biến đường thẳng thành đường thẳng; biến tia thành tia; biến đoạn thẳng thành đoạn thẳng.

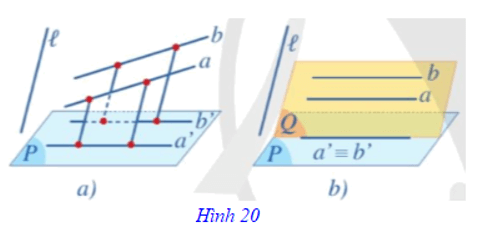
Định lí:

⦁ Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau. (Hình 20)

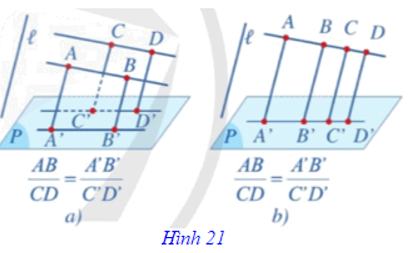
⦁ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng. (Hình 21)

Chú ý: Đối với hình chiếu song song của đường tròn, người ta chứng minh được rằng: Hình chiếu song song của một đường tròn trên một mặt phẳng theo phương ℓ cho trước là một đường elip hoặc một đường tròn, hoặc đặc biệt có thể là một đoạn thẳng.

6.2. Hình biểu diễn của một hình không gian

a) Khái niệm

Hình biểu diễn của một hình ℋ trong không gian là hình chiếu song song của hình ℋ trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.

Chú ý: Muốn vẽ đúng hình biểu diễn của một hình trong không gian, ta phải áp dụng các tính chất của phép chiếu song song.

b) Hình biểu diễn của một số hình khối đơn giản

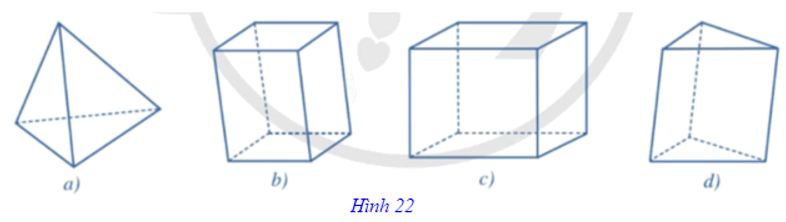
Các hình sau đây thường được sử dụng làm hình biểu diễn của: hình tứ diện (Hình 22a); hình hộp (Hình 22b); hình hộp chữ nhật (Hình 22c); hình lăng trụ tam giác (Hình 22d).

Chú ý:

1)

⦁ Một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tùy ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông,...).

⦁ Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tùy ý cho trước (có thể là hình bình hành, hình vuông, hình thoi, hình chữ nhật,...).

⦁ Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn cho một hình thang tùy ý cho trước, sao cho tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.

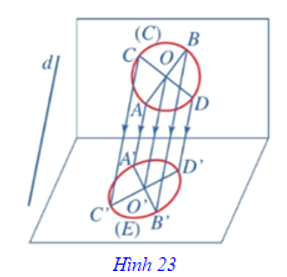
⦁ Ta thường dùng đường elip làm hình biểu diễn của đường tròn, tâm của elip biểu diễn cho tâm của đường tròn (Hình 23).

2) Phép chiếu song song nói chung không giữ nguyên tỉ số của hai đoạn thẳng không nằm trên hai đường thẳng song song (hay không cùng nằm trên một đường thẳng) và không giữ nguyên độ lớn của một góc. Từ đó suy ra nếu trên hình ℋ có hai đoạn thẳng không nằm trên hai đường thẳng song song thì tỉ số của chúng không nhất thiết phải giữ nguyên trên hình biểu diễn. Cũng như vậy, độ lớn của một góc trên hình ℋ không nhất thiết được giữ nguyên trên hình biểu diễn.

Bài tập tổng hợp Toán 11 Chương 4

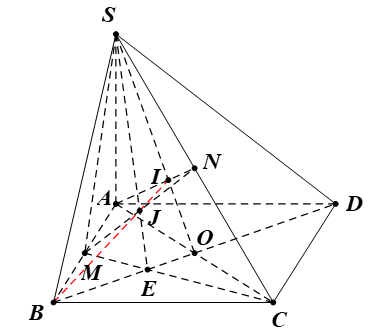
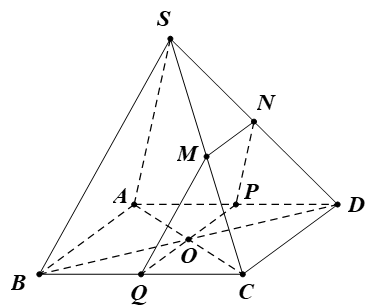
Bài 1. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của các cạnh SC và SD. Gọi O là giao điểm AC và BD.

a) Tìm giao tuyến của các cặp mặt phẳng (SAC) và (SBD); (SAB) và (SCD).

b) Tìm giao điểm P của đường thẳng BN với mặt phẳng (SAC).

c) Gọi Q và R lần lượt là trung điểm của SA và SB. Chứng minh rằng bốn điểm M, N, Q, R cùng nằm trên một mặt phẳng.

Hướng dẫn giải

a) Trong (ABCD): O là giao điểm AC và BD.

Mà AC ⊂ (SAC) và BD ⊂ (SBD).

Do đó O cùng thuộc hai mặt phẳng (SAC) và (SBD).

Mà S cùng thuộc hai mặt phẳng (SAC) và (SBD).

Vậy SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).

Trong (ABCD): gọi E là giao điểm của AB và CD.

Mà AB ⊂ (SAB) và CD ⊂ (SCD).

Do đó E cùng thuộc hai mặt phẳng (SAB) và (SCD).

Mà S cùng thuộc hai mặt phẳng (SAB) và (SCD).

Vậy SE là giao tuyến của hai mặt phẳng (SAC) và (SBD).

b) Trong (SBD): gọi P là giao điểm của SO và BN.

Mà SO ⊂ (SAC).

Vậy P là giao điểm của đường thẳng BN và mặt phẳng (SAC).

c) Trong (SCD): gọi T là giao điểm của MN và SE.

Tam giác SCD có M, N lần lượt là trung điểm của SC, SD.

Suy ra MN là đường trung bình của tam giác SCD.

Do đó MN // CD.

Xét tam giác SDE, có: MT // DE (chứng minh trên) và N là trung điểm SD.

Suy ra T là trung điểm SE.

Tương tự, ta có QR là đường trung bình của tam giác SAB.

Do đó QR // AB.

Xét tam giác SAE, có: QT // AE (chứng minh trên) và Q là trung điểm SA.

Suy ra QR đi qua trung điểm T của SE.

Như vậy, bốn điểm M, N, Q, R cùng thuộc một mặt phẳng, mặt phẳng này là (QNT)

Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của đoạn AB và SC.

a) Xác định giao điểm I của đường thẳng AN và mặt phẳng (SBD).

b) Xác định giao điểm J của đường thẳng MN và mặt phẳng (SBD).

c) Chứng minh ba điểm I, J, B thẳng hàng.

Hướng dẫn giải

a) Trong (ABCD): gọi O là giao điểm của AC và BD.

Trong (SAC): gọi I là giao điểm của AN và SO.

Mà SO ⊂ (SBD).

Vậy I là giao điểm của đường thẳng AN và mặt phẳng (SBD).

b) Trong (ABCD): gọi E là giao điểm của MC và BD.

Trong (SMC): gọi J là giao điểm của MN và SE.

Mà SE ⊂ (SBD).

Vậy J là giao điểm của đường thẳng MN và mặt phẳng (SBD).

c) Ta có ba điểm I, J, B lần lượt nằm trên các đường thẳng AN, MN, AM.

Suy ra ba điểm I, J, B đều thuộc mặt phẳng (AMN).

Mà ba điểm I, J, B đều thuộc (SBD).

Do đó ba điểm I, J, B đều nằm trên đường giao tuyến của hai mặt phẳng (AMN) và (SBD).

Vậy ba điểm I, J, B thẳng hàng.

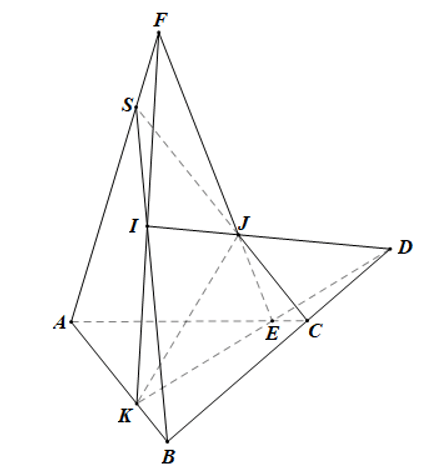
Bài 3. Cho tứ diện S.ABC. Gọi I, J, K lần lượt là các điểm nằm trên các cạnh SB, SC và AB sao cho IJ không song song với BC, IK không song song với SA.

a) Tìm giao điểm D của mặt phẳng (IJK) và đường thẳng BC.

b) Gọi E là giao điểm của DK và AC. Chứng minh ba đường thẳng SA, KI, EJ đồng quy.

Hướng dẫn giải

a) Trong (SBC): gọi D là giao điểm của IJ và BC.

Mà IJ ⊂ (IJK).

Vậy D là giao điểm của mặt phẳng (IJK) và đường thẳng BC.

b) Trong (ABC): gọi F là giao điểm của IK và SA.

Mà IK ⊂ (IJK) và SA ⊂ (SAC).

Suy ra F đều thuộc hai mặt phẳng (IJK) và (SAC)   (1)

Lại có E là giao điểm của DK và AC.

Mà DK ⊂ (IJK) và AC ⊂ (SAC).

Suy ra E đều thuộc hai mặt phẳng (IJK) và (SAC)   (2)

Mặt khác, J là giao điểm của ID và SC.

Mà ID ⊂ (IJK) và SC ⊂ (SAC).

Suy ra J đều thuộc hai mặt phẳng (IJK) và (SAC)    (3)

Từ (1), (2), (3), suy ra ba điểm F, E, J đều nằm trên đường giao tuyến của hai mặt phẳng (IJK) và (SAC).

Khi đó ba điểm F, E, J thẳng hàng.

Vậy ba đường thẳng SA, KI, EJ đồng quy tại F.

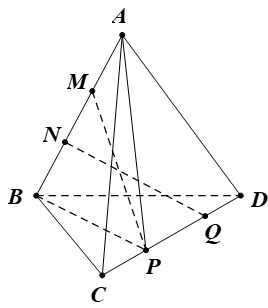
Bài 4. Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MP và NQ.

Hướng dẫn giải

Ta có N = AB ∩ NQ.

Suy ra N là giao điểm của đường thẳng NQ và mặt phẳng (ABP).

Do đó Q không thuộc mặt phẳng (ABP).

Mà M, N, P đều thuộc mặt phẳng (ABP).

Suy ra bốn điểm M, N, P, Q không đồng phẳng.

Vậy hai đường thẳng MP và NQ chéo nhau.

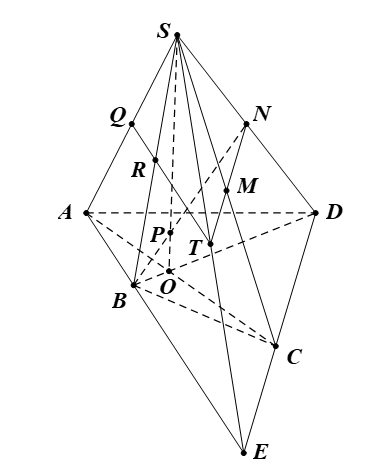
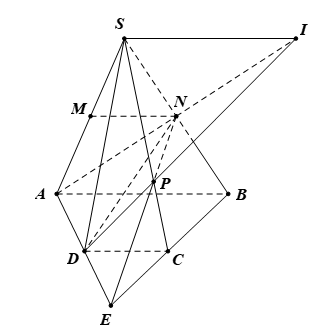
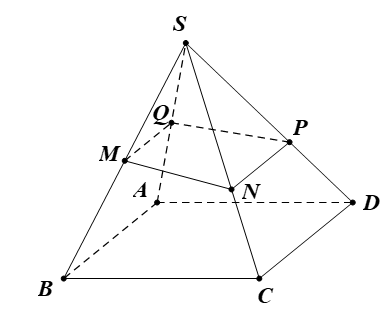
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình thang (đáy lớn AB, đáy nhỏ CD). Gọi M, N lần lượt là trung điểm của SA và SB. Gọi P là giao điểm của SC và (AND). Gọi I là giao điểm của AN và DP. Hỏi tứ giác SABI là hình gì?

Hướng dẫn giải

Trong (ABCD): gọi E = AD ∩ BC.

Mà AD ⊂ (AND) và BC ⊂ (SBC).

Suy ra E ∈ (AND) và E ∈ (SBC).

Trong (SBC): gọi P = SC ∩ NE.

Mà NE ⊂ (AND).

Vì vậy P là giao điểm của đường thẳng SC và mặt phẳng (AND).

Ta có I = AN ∩ DP.

Mà AN ⊂ (SAB) và DP ⊂ (SCD).

Suy ra I cùng thuộc hai mặt phẳng (SAB) và (SCD).

Mà S cùng thuộc hai mặt phẳng (SAB) và (SCD).

Do đó SI = (SAB) ∩ (SCD).

Lại có AB = (SAB) ∩ (ABCD) và CD = (SCD) ∩ (ABCD).

Mà trong (ABCD), ta lại có AB // CD (do ABCD là hình thang với đáy lớn AB, đáy nhỏ CD).

Do đó SI // AB // CD.

Tam giác SAB có M, N lần lượt là trung điểm của SA, SB.

Suy ra MN là đường trung bình của tam giác SAB.

Do đó MN // AB.

Vì vậy MN // SI (do AB // SI).

Mà N là trung điểm SA.

Do đó M là trung điểm AI.

Tứ giác SABI có hai đường chéo SB và AI cắt nhau tại trung điểm M của mỗi đường.

Vậy tứ giác SABI là hình bình hành.

Bài 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi (α) là mặt phẳng đi qua trung điểm M của cạnh SB, song song với cạnh AB và cắt các cạnh SA, SD, SC lần lượt tại các điểm Q, P, N. Chứng minh tứ giác MNPQ là hình thang.

Hướng dẫn giải

Ta có AB // (α) và M ∈ (α).

Mà AB ⊂ (SAB).

Suy ra (α) ∩ (SAB) = MQ, với MQ // AB và Q ∈ SA.

Lại có CD // AB (do tứ giác ABCD là hình bình hành).

Suy ra CD // MQ   (1)

Mà MQ ⊂ (α).

Do đó CD // (α).

Mà (α) ∩ (SCD) = NP.

Vì vậy CD // NP   (2)

Từ (1), (2), suy ra MQ // NP.

Vậy tứ giác MNPQ là hình thang.

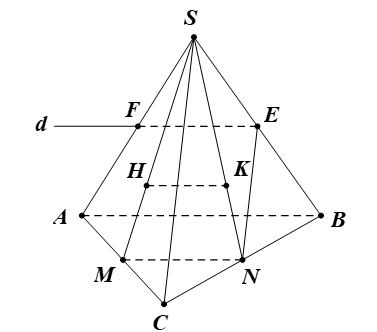
Bài 7. Cho hình chóp S.ABC. Gọi M, N, E lần lượt là trung điểm của AC, BC, SB. Gọi H, K lần lượt là trọng tâm của các tam giác SAC và SBC.

a) Xác định giao tuyến d của hai mặt phẳng (MNE) và (SAB).

b) Chứng minh HK // (SAB).

c) Chứng minh HK // d.

Hướng dẫn giải

a) Tam giác ABC có M, N lần lượt là trung điểm của các cạnh AC và BC.

Suy ra MN là đường trung bình của tam giác ABC.

Do đó MN // AB.

Ta có E đều thuộc hai mặt phẳng (MNE) và (SAB).

Mà MN // AB (chứng minh trên); MN ⊂ (MNE) và AB ⊂ (SAB).

Suy ra giao tuyến của hai mặt phẳng (MNE) và (SAB) là đường thẳng d đi qua E và d // MN // AB.

b) Tam giác SAC có H là trọng tâm và M là trung điểm AC.

Suy ra $\frac{SH}{SM}=\frac{2}{3}$.

Chứng minh tương tự, ta được $\frac{SK}{SN}=\frac{2}{3}$.

Do đó $\frac{SH}{SM}=\frac{SK}{SN}=\frac{2}{3}$.

Áp dụng định lí Thales, ta được HK // MN.

Mà MN ⊂ (SAB).

Vậy HK // (SAB)   (1)

c) Trong (SAB): gọi F = d ∩ SA.

Ta có HK // MN (chứng minh trên).

Mà MN ⊂ (MNEF).

Suy ra HK // (MNEF)    (2)

Ta lại có (SAB) ∩ (MNEF) = EF (theo kết quả câu a)   (3)

Từ (1), (2), (3), ta thu được HK // EF.

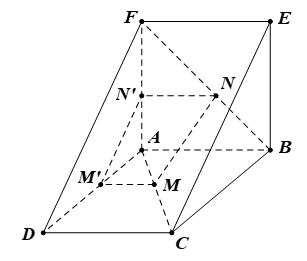
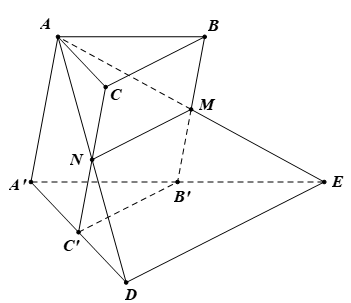
Bài 8. Cho hai hình vuông ABCD và ABEF thuộc hai mặt phẳng phân biệt. Trên các đường chéo AC và BF, lấy các điểm M, N sao cho AM = BN. Từ M, N, vẽ các đường thẳng song song với AB, lần lượt cắt AD và AF tại các điểm M’ và N’. Chứng minh:

a) (ADF) // (BCE).

b) (DEF) // (MM’N’N).

Hướng dẫn giải

a) Ta có AD // BC (do ABCD là hình vuông).

Mà BC ⊂ (BCE), suy ra AD // (BCE)   (1)

Chứng minh tương tự, ta được AF // (BCE)    (2)

Trong (ADF): AD ∩ AF = A   (3)

Từ (1), (2), (3), ta thu được (ADF) // (BCE).

b) Ta có hai hình vuông ABCD và ABEF có cùng cạnh AB.

Do đó hai hình vuông ABCD và ABEF bằng nhau.

Vì vậy hai đường chéo AC và BF bằng nhau hay AC = BF  (1)

Do MM’ // CD (giả thiết) nên áp dụng định lí Thales, ta được: $\frac{A{M}^{\text{'}}}{AD}=\frac{AM}{AC}$  (2)

Chứng minh tương tự, ta được: $\frac{A{N}^{\text{'}}}{AF}=\frac{BN}{BF}$   (3)

Lại có AM = BN (giả thiết)   (4)

Từ (1), (2), (3), (4), suy ra $\frac{A{M}^{\text{'}}}{AD}=\frac{A{N}^{\text{'}}}{AF}$.

Áp dụng định lí Thales đảo, ta được M’N’ // DF.

Mà M’N’ ⊂ (MM’N’N).

Do đó DF // (MM’N’N)  (*)

Ta có NN’ // AB (giả thiết) và AB // EF (ABEF là hình vuông).

Suy ra NN’ // EF.

Mà NN’ ⊂ (MM’N’N).

Do đó EF // (MM’N’N)  (**)

Trong (DEF): DF ∩ EF = F  (***)

Từ (*), (**), (***), ta thu được (DEF) // (MM’N’N).

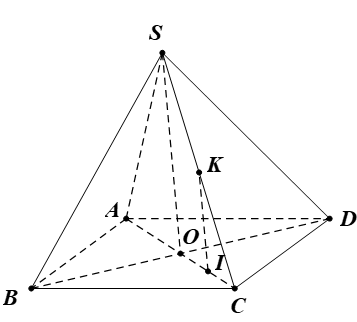
Bài 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc đoạn OC (I ≠ O và I ≠ C). Gọi K là giao điểm của đường thẳng SC và mặt phẳng (P). Chứng minh IK // SO.

Hướng dẫn giải

Ta có K là giao điểm của đường thẳng SC và mặt phẳng (P).

Suy ra K đều thuộc hai mặt phẳng (SAC) và (P).

Mà I đều thuộc hai mặt phẳng (SAC) và (P).

Do đó KI là giao tuyến của hai mặt phẳng (SAC) và (P).

Lại có (SBD) // (P) (giả thiết) và (SAC) ∩ (SBD) = SO.

Vậy theo định lí 3, ta có IK // SO.

Bài 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi (α) là mặt phẳng đi qua O và song song với (SAB), mặt phẳng (α) cắt các đường thẳng SC, SD, AD, BC lần lượt tại các điểm M, N, P, Q. Chứng minh N là trung điểm SD.

Hướng dẫn giải

Qua điểm O, ta dựng PQ // AB, với P ∈ AD và Q ∈ BC.

Khi đó P, Q lần lượt là trung điểm của AD và BC.

Do đó CQ = BQ.

Vì tứ giác ABCD là hình bình hành nên AB // CD // PQ.

Khi đó theo Hệ quả 2 của Định lí 2, ta có duy nhất một mặt phẳng (β) chứa CD và song song với (SAB) và (α).

Ta có:

⦁ Đường thẳng CB cắt ba mặt phẳng song song (β), (α) và (SAB) lần lượt tại C, Q, B.

⦁ Đường thẳng DS cắt ba mặt phẳng song song (β), (α) và (SAB) lần lượt tại D, N, S.

Áp dụng định lí Thalès trong không gian, ta có: $\frac{QB}{NS}=\frac{CQ}{DN}$.

Suy ra $\frac{DN}{NS}=\frac{CQ}{QB}=1$.

Vậy N là trung điểm SD.

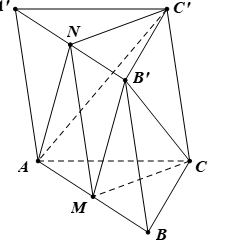
Bài 11. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. Chứng minh:

a) Tứ giác MNC’C là hình bình hành.

b) (B’MC) // (ANC’).

Hướng dẫn giải

a) Hình bình hành ABB’A’ có: M, N là trung điểm AB, A’B’.

Suy ra MN là đường trung bình của hình bình hành ABB’A’.

Do đó MN // BB’ và MN = BB’.

Mà BB’ // CC’ và BB’ = CC’ (do tứ giác BCC’B’ là hình bình hành).

Suy ra MN // CC’ và MN = CC’.

Vậy tứ giác MNC’C là hình bình hành.

b) Ta có ABB’A’ là hình bình hành.

Suy ra A’B’ // AB và A’B’ = AB.

Mà M, N lần lượt là trung điểm của AB, A’B’.

Do đó B’N // AM và B’N = AM.

Vì vậy tứ giác AMB’N là hình bình hành.

Khi đó AN // B’M.

Suy ra AN // (B’MC)   (1)

Ta có tứ giác MNC’C là hình bình hành, suy ra NC’ // MC.

Do đó NC’ // (B’MC)  (2)

Trong (ANC’) có N = AN ∩ NC’   (3)

Từ (1), (2), (3), ta thu được (ANC’) // (B’MC).

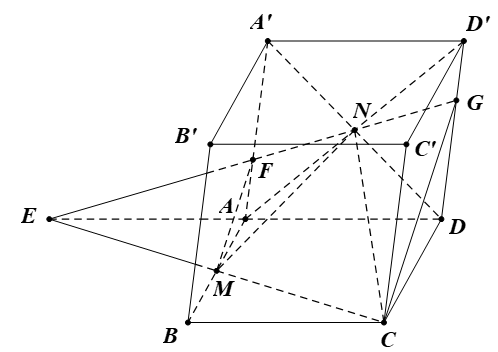
Bài 12. Cho hình hộp ABCD.A’B’C’D’. Gọi M là trung điểm AB và N là giao điểm của A’D và AD’.

a) Xác định giao tuyến d của hai mặt phẳng (CMN) và (ADD’A’).

b) Gọi F, G lần lượt là giao điểm của đường thẳng d với các đường thẳng AA’ và DD’. Chứng minh MF // CG.

Hướng dẫn giải

a) Trong (ABCD): gọi E = CM ∩ AD.

Mà CM ⊂ (CMN) và AD ⊂ (ADD’A’).

Suy ra E đều thuộc (CMN) và (ADD’A’)   (1)

Lại có N là giao điểm của AD’ và A’D (giả thiết).

Suy ra N nằm trên mặt phẳng (ADD’A’).

Do đó N đều thuộc (CMN) và (ADD’A’)   (2)

Từ (1), (2), ta thu được NE là giao tuyến của (CMN) và (ADD’A’) hay d ≡ NE.

b) Ta có M ∈ AB (giả thiết).

Mà AB ⊂ (ABB’A’), suy ra M ∈ (ABB’A’).

Lại có M ∈ (CMN) nên M đều thuộc (CMN) và (ABB’A’)   (3)

Ta có F ∈ NE và F ∈ AA’.

Mà NE ⊂ (CMN) và AA’ ⊂ (ABB’A’).

Suy ra F đều thuộc hai mặt phẳng (CMN) và (ABB’A’)   (4)

Từ (3), (4), suy ra MF là giao tuyến của (CMN) và (ABB’A’).

Chứng minh tương tự, ta được CG là giao tuyến của (CMN) và (CDD’C).

Ta có (ABB’A’) // (CDD’C) (tính chất hình hộp).

Mà (CMN) ∩ (ABB’A’) = MF và (CMN) ∩ (CDD’C) = CG.

Vậy MF // CG.

Bài 13. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh BB’, CC’.

a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (A’B’C’).

b) Chứng minh d // (ABC).

Hướng dẫn giải

a) Trong (AA’C’C): gọi D = A’C’ ∩ AN.

Mà A’C’ ⊂ (A’B’C’) và AN ⊂ (AMN).

Suy ra D đều thuộc hai mặt phẳng (AMN) và (A’B’C’)   (1)

Trong (AA’B’B): gọi E = AM ∩ A’B’.

Mà AM ⊂ (AMN) và A’B’ ⊂ (A’B’C’).

Suy ra E đều thuộc hai mặt phẳng (AMN) và (A’B’C’)   (2)

Từ (1), (2), suy ra DE là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’) hay d ≡ DE.

b) Hình bình hành BCC’B’, có: M, N lần lượt là trung điểm của BB’, CC’.

Suy ra MN là đường trung bình của hình bình hành BCC’B’.

Do đó MN // B’C’ // BC.

Ta có:

⦁ MN = (AMN) ∩ (MNC’B’);

⦁ B’C’ = (A’B’C’) ∩ (MNC’B’);

⦁ DE = (AMN) ∩ (A’B’C’);

⦁ MN // B’C’ (chứng minh trên).

Suy ra DE // MN // B’C’.

Mà B’C’ // BC (chứng minh trên).

Do đó DE // BC.

Mà BC ⊂ (ABC).

Vậy DE // (ABC) hay d // (ABC).

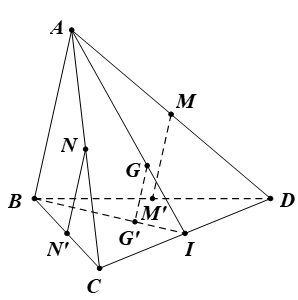
Bài 14. Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ACD.

a) Chứng minh hình chiếu song song G’ của điểm G trên mặt phẳng (BCD) theo phương chiếu AB là trọng tâm của tam giác BCD.

b) Gọi M, N lần lượt là trung điểm của AD và AC. Tìm hình chiếu song song của các điểm M, N theo phép chiếu nói trên.

Hướng dẫn giải

a) Gọi I là trung điểm của CD.

Ta có hình chiếu song song của đoạn IA trên mặt phẳng (BCD) theo phương AB là đoạn IB.

Vì phép chiếu song song bảo toàn tính thẳng hàng và thứ tự của ba điểm A, G, I nên ảnh G’ của G qua phép chiếu song song trên mặt phẳng (BCD) theo phương AB nằm trên đoạn BI và nằm giữa hai điểm B, I, đồng thời GG’ // AB.

Tam giác IAB, có: $\frac{I{G}^{\text{'}}}{IB}=\frac{IG}{IA}=\frac{1}{3}$ (do G là trọng tâm của tam giác ACD).

Mà I là trung điểm CD.

Vậy G’ là trọng tâm của tam giác BCD.

b) Gọi M’, N’ lần lượt là hình chiếu song song của M, N trên mặt phẳng (BCD) theo phương AB.

Ta có đoạn BD là hình chiếu song song của đoạn AD trên mặt phẳng (BCD) theo phương AB.

Mà M là trung điểm AD.

Do đó ảnh M’ của M qua phép chiếu song song trên mặt phẳng (BCD) theo phương AB là trung điểm của đoạn BD.

Chứng minh tương tự, ta được ảnh N’ của N qua phép chiếu song song trên mặt phẳng (BCD) theo phương AB là trung điểm của đoạn BC.

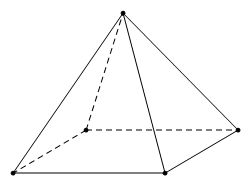
Bài 15. Vẽ hình biểu diễn của một chiếc hộp đựng bánh ít trong hình vẽ dưới đây:

Hướng dẫn giải

Hình biểu diễn của một chiếc hộp đựng bánh ít:

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Hai đường thẳng song song trong không gian

Lý thuyết Bài 3: Đường thẳng và mặt phẳng song song

Lý thuyết Bài 4: Hai mặt phẳng song song

Lý thuyết Bài 5: Hình lăng trụ và hình hộp

Lý thuyết Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian