10 câu hỏi trắc nghiệm thuộc Dạng 2: Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều có đáp án

Trắc nghiệm Toán 8 Bài 39. Hình chóp tứ giác đều có đáp án

Dạng 2: Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều có đáp án

177 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Diện tích xung quanh của hình chóp tứ giác đều bằng

A. Tổng diện tích 4 mặt bên;

B. Tổng diện tích tất cả các mặt;

C. Tích của nửa chu vi đáy với trung đoạn của hình chóp đó;

D. Cả A, C đều đúng.

Xem đáp án

Đáp án đúng là: D

Ta có diện tích xung quanh của hình chóp tứ giác đều chính là tổng diện tích của 4 mặt bên và nó cũng được tính bằng tích của nửa chu vi đáy với trung đoạn của hình chóp đó nên D đúng.

Câu 2:

Một hình chóp tứ giác đều có thể tích bằng 144 cm³, chiều cao bằng 12 cm. Độ dài cạnh đáy của hình chóp là

A. 4 cm;

B. 5 cm;

C. 6 cm;

D. 7 cm.

Xem đáp án

Đáp án đúng là: C

Ta có $V = \frac{1}{3} \cdot S \cdot h$ .

Suy ra diện tích đáy $S = \frac{3V}{h} = \frac{3 \cdot 144}{12} = 36$ (cm²).

Vì 6² = 36 nên độ dài cạnh đáy là 6 cm.

Câu 3:

Cho hình chóp tứ giác đều có cạnh đáy bằng 3 cm, đường cao của tam giác mặt bên kẻ từ đỉnh của hình chóp bằng 7 cm. Diện tích xung quanh của hình chóp tứ giác đều là

A. 22 cm²;

B. 24 cm²;

C. 34 cm²;

D. 42 cm².

Xem đáp án

Đáp án đúng là: D

Nửa chu vi đáy của hình chóp tứ giác đều là:

p = (3 ⋅ 4) : 2 = 6 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là:

S_xq = p ⋅ d = 6 ⋅ 7 = 42 (cm²).

Câu 4:

Cho hình chóp tứ giác đều có diện tích xung quanh là 84 cm², độ dài trung đoạn là 14 cm. Độ dài cạnh đáy của hình chóp tứ giác đều là:

A. 2 cm;

B. 3 cm;

C. 4 cm;

D. 5 cm.

Xem đáp án

Đáp án đúng là: B

Ta có: S_xq = p ⋅ d.

Suy ra nửa chu vi đáy là p = S_xq : d = 84 : 14 = 6 (cm).

Khi đó, chu vi đáy là 6 ∙ 2 = 12 (cm).

Cạnh đáy của hình chóp tứ giác đều là:

12 : 4 = 3 (cm).

Câu 5:

Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 4 cm, cạnh bên bằng 8 cm. Diện tích xung quanh của hình chóp tứ giác đều là:

A. 64 cm²;

8 \sqrt{60}

cm²;

\sqrt{60}

cm²;

D. 15 cm².

Xem đáp án

Đáp án đúng là: B

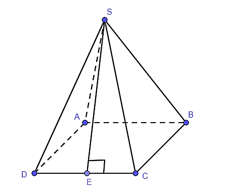
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 4 cm, cạnh bên bằng 8 cm. Diện tích xung quanh của hình chóp tứ giác đều là: (ảnh 1)

Gọi SE là một trung đoạn của hình chóp tứ giác đều.

Vì tam giác SDC là tam giác cân nên E là trung điểm của DC.

Suy ra $DE = \frac{DC}{2} = \frac{4}{2} = 2$ (cm).

Tam giác SED vuông tại E nên SE² + DE² = SD² (định lí Pythagore).

Suy ra SE²= SD²– DE²= 8² – 2² = 60.

Do đó, SE = $\sqrt{60}$ (cm).

Nửa chu vi đáy của hình chóp tứ giác đều là:

(4 ⋅ 4) : 2 = 8 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là:

S_xq = p ⋅ d = 8 ⋅ $\sqrt{60}$ = $8 \sqrt{60}$ (cm²).

Câu 6:

Cho hình chóp tứ giác đều S.MNPQ có cạnh bên bằng 13 cm, cạnh đáy bằng cm. Thể tích của hình chóp tứ giác đều S.MNPQ là

A. 200 cm³;

B. 240 cm³;

C. 350 cm³;

D. 390 cm³.

Xem đáp án

Đáp án đúng là: A

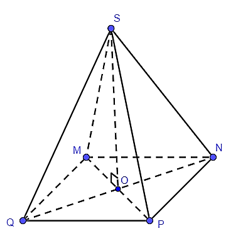
Cho hình chóp tứ giác đều S.MNPQ có cạnh bên bằng 13 cm, cạnh đáy bằng cm. Thể tích của hình chóp tứ giác đều S.MNPQ là A. 200 cm3; B. 240 cm3; C. 350 cm3; D. 390 cm3. (ảnh 1)

Gọi SO là đường cao của hình chóp S.MNPQ.

Tam giác MPQ vuông tại Q nên MQ² + QP² = MP² (định lý Pythagore).

Suy ra MP² = ${(5 \sqrt{2})}^{2} + {(5 \sqrt{2})}^{2} = 100$ .

Do đó, MP = 10 (cm).

Vì O là giao điểm hai đường chéo MP và NQ nên O là trung điểm MP.

Suy ra $MO = \frac{MP}{2} = \frac{10}{2} = 5$ (cm).

Tam giác SOM vuông tại O nên MO² + SO² = SM² (định lý Pythagore).

Suy ra SO² = SM² – MO² = 13² – 5² =144.

Do đó, SO = 12 (cm).

Diện tích đáy MNPQ là:

S = ${(5 \sqrt{2})}^{2} = 50$ (cm²).

Thể tích hình chóp tứ giác đều S.MNPQ là:

$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot 50 \cdot 12 = 200$ (cm³).

Câu 7:

Thể tích hình chóp tứ giác đều S.MNPQ có trung đoạn bằng 5 cm và diện tích xung quanh bằng 80 cm² là

A. 46 cm³;

B. 52 cm³;

C. 64 cm³;

D. 75 cm³.

Xem đáp án

Đáp án đúng là: C

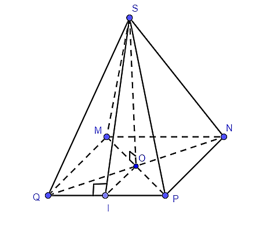
Thể tích hình chóp tứ giác đều S.MNPQ có trung đoạn bằng 5 cm và diện tích xung quanh bằng 80 cm2 là A. 46 cm3; B. 52 cm3; C. 64 cm3; D. 75 cm3. (ảnh 1)

Ta có: S_xq = p ⋅ d .

Suy ra p = S_xq : d = 80 : 5 = 16 (cm).

Độ dài cạnh đáy của hình chóp tứ giác đều là:

(16 ∙ 2) : 4 = 8 (cm).

Gọi SO là đường cao và SI là một trung đoạn của hình chóp S.MNPQ.

Khi đó, OI là đường trung bình của tam giác MQP.

Suy ra OI = MQ : 2 = 8 : 2 = 4 (cm).

Tam giác SOI vuông tại O nên SO² + OI² = SI².

Suy ra SO² = SI² – OI² = 5²– 4²= 9.

Do đó, SO = 3 (cm).

Diện tích đáy MNPQ là:

S = 8² = 64 (cm²).

Thể tích hình chóp tứ giác đều S.MNPQ là:

$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot 64 \cdot 3 = 64$ (cm³).

Câu 8:

Cho hình chóp tứ giác đều có thể tích là 63 cm³, diện tích đáy là 21 cm². Chiều cao của hình chóp tứ giác đều là

A. 5 cm;

B. 7 cm;

C. 6 cm;

D. 9 cm.

Xem đáp án

Đáp án đúng là: D

Ta có: $V = \frac{1}{3} \cdot S \cdot h$ .

Suy ra $h = \frac{3V}{S} = \frac{3 \cdot 63}{21} = 9$ (cm).

Câu 9:

Một hình chóp tứ giác đều có thể tích bằng 50 cm³, chiều cao hình chóp bằng 6 cm, chiều cao mặt bên bằng 5 cm. Diện tích xung quanh hình chóp đó là

A. 50 cm²;

B. 10 cm²;

C. 40 cm²;

D. 20 cm².

Xem đáp án

Đáp án đúng là: A

Ta có: $V = \frac{1}{3} \cdot S \cdot h$ .

Suy ra diện tích đáy của hình chóp tứ giác đều $S = \frac{3V}{h} = \frac{3 \cdot 50}{6} = 25$ (cm²).

Vì 5² = 25 nên độ dài cạnh đáy là 5 cm.

Diện tích một mặt bên là:

$\frac{1}{2} \cdot 5 \cdot 5 = \frac{25}{2}$ (cm²).

Diện tích xung quanh của hình chóp tứ giác đều là:

$4 \cdot \frac{25}{2} = 50$ (cm²).

Câu 10:

Thể tích của hình chóp tứ giác đều có cạnh đáy là 4 cm và chiều cao là 9 cm là

A. 48 cm³;

B. 144 cm³;

C. 84 cm³;

D. 100 cm³.

Xem đáp án

Đáp án đúng là: A

Diện tích đáy của hình chóp tứ giác đều là:

S = 4² = 16 (cm²).

Thể tích của hình chóp tứ giác đều là:

$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot 16 \cdot 9 = 48$ (cm³).

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 39. Hình chóp tứ giác đều có đáp án

Dạng 2: Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương