Trắc nghiệm Toán 8 Bài 37. Hình đồng dạng có đáp án
Dạng 1. Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh
-
147 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho các khẳng định sau:
(I) Hai hình đồng dạng phối cảnh (hay vị tự) không là hai hình đồng dạng.
(II) Nếu điểm O là tâm đồng dạng phối cảnh của hai đoạn thẳng AB và A'B' đồng dạng phối cảnh thì AB // A'B'.
(III) Hình H' gọi là đồng dạng với hình H nếu hình H bằng một hình nào đó đồng dạng phối cảnh với hình H.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Khẳng định (I) sai: Hai hình đồng dạng phối cảnh (hay vị tự) là hai hình đồng dạng.
Khẳng định (II) sai vì: Nếu điểm O là tâm đồng dạng phối cảnh của hai đoạn thẳng AB và A'B' đồng dạng phối cảnh thì AB // A'B' hoặc AB trùng với A'B'.
Khẳng định (III) đúng.
Vậy chỉ có 1 khẳng định đúng trong các khẳng định trên.
Câu 2:
Cho các hình sau:
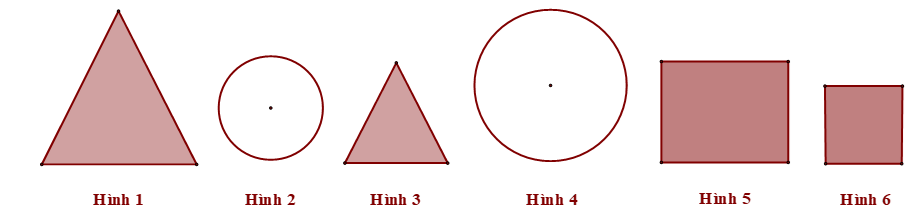
Có bao nhiêu cặp hình đồng dạng trong hình trên?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Các cặp hình đồng dạng là: Hình 1 và Hình 3; Hình 2 và Hình 4.
Hình 5 và hình 6 không phải là cặp hình đồng dạng vì hình 5 là hình chữ nhật, hình 6 là hình vuông.
Vậy có 2 cặp hình đồng dạng.
Câu 3:
Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Áp dụng lí thuyết, ta có: Hình H' đồng dạng với hình H nếu hình H' bằng một hình nào đó đồng dạng phối cảnh với hình H.
Do đó, phát biểu “Hình H' gọi là đồng dạng với hình H nếu H' bằng H hoặc bằng một hình phóng to hay thu nhỏ của H” là phát biểu đúng.
Câu 4:
Cho hình vẽ:
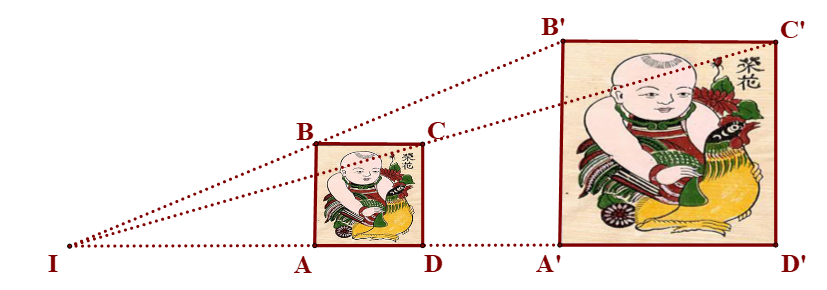
Biết các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng IA', IB', IC', ID'.
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có:
+ Các đường thẳng AA', BB', CC', DD' cùng đi qua điểm I.
+ Vì A, B, C, D lần lượt là trung điểm của các đoạn thẳng IA', IB', IC', ID' nên ta có:
Do đó, hai tứ giác ABCD và A'B'C'D' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.
Hai đoạn thẳng AB và A'B' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh;
Hai đoạn thẳng BD và B'D' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.
Vậy khẳng định sai là “Hai đoạn thẳng BB' và AA' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh”.
Câu 5:
Cho hai tứ giác A'B'C'D' và ABCD đồng dạng phối cảnh với nhau. O là tâm đồng dạng phối cảnh, tỉ số .
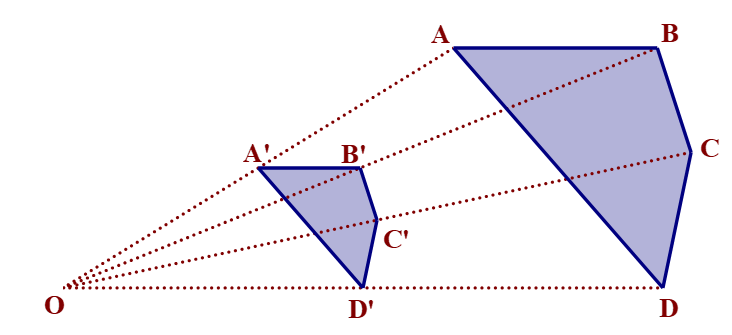
Biết AB = 3 cm; BC = 1,5 cm; CD = 2 cm; AD = 4 cm.
Chu vi tứ giác A'B'C'D' là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì hai tứ giác A'B'C'D' và ABCD đồng dạng phối cảnh với nhau. O là tâm đồng dạng phối cảnh, tỉ số nên ta có:
Chu vi tứ giác A'B'C'D' là:
A'B' + B'C' + C'D' + D'A' = 1,5 cm + 0,75 cm + 1 cm + 2 cm = 5,25 cm.
Vậy chu vi tứ giác A'B'C'D' là 5,25 cm.
Câu 6:
Cho tam giác ABC có AB = 13 cm, BC = 14 cm, CA = 15 cm và D là một điểm phân biệt. Giả sử tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC với điểm D là tâm đồng dạng phối cảnh, tỉ số . Độ dài cạnh B'C' là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Vì tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC với điểm D là tâm đồng dạng phối cảnh, tỉ số nên ta có:
cm.
Vậy độ dài cạnh B'C' là 11,2 cm.
Câu 7:
Cho tam giác ABC có AB = 13, BC = 14, CA = 15 và E là một điểm phân biệt. Giả sử tam giác A''B''C'' là hình đồng dạng phối cảnh của tam giác ABC với điểm E là tâm đồng dạng phối cảnh, tỉ số . Chu vi của tam giác A''B''C'' là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Vì tam giác A''B''C'' là hình đồng dạng phối cảnh của tam giác ABC với điểm E là tâm đồng dạng phối cảnh, tỉ số nên ta có:
.
Chu vi tam giác A''B''C'' là: 10,4 + 11,2 + 12 = 33,6.
Câu 8:
Cho tam giác ABC có E, F lần lượt là trung điểm của BC, AC. Các điểm M, P, R, Q lần lượt nằm trên AB, BE, EF, FA sao cho .
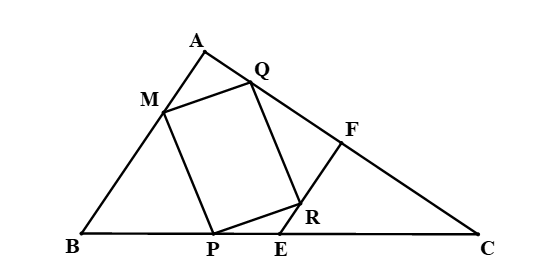
Cho các khẳng định sau:
(I) Hai đoạn thẳng FE và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh.
(II) Hai đoạn thẳng MP và AE đồng dạng phối cảnh, điểm B là tâm đồng dạng phối cảnh và .
(III) Hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
*) Ta có:
+ Hai đường thẳng AF và BE cùng đi qua điểm C.
+ (vì F, F lần lượt là trung điểm của BC, AC).
Þ Hai đoạn thẳng FE và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh.
Þ Khẳng định (I) đúng.
*)
Vì do đó khẳng định II sai.
*) Ta có:
+ Hai đường thẳng BP và FR cùng đi qua điểm E.
+)
Þ Hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh.
Vậy khẳng định (I) và (II) đúng.
Câu 9:
Cho tam giác ABC với trọng tâm O. Lấy điểm A', B', C' lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
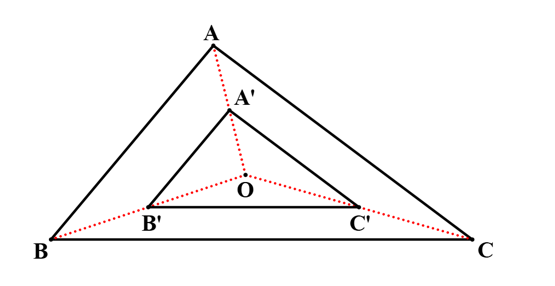
Ta có:
+) Ta thấy ba đường thẳng AA', BB', CC' cùng đi qua điểm O.
+) Vì A', B', C' lần lượt là trung điểm của các đoạn thẳng OA, OB, OC nên
Suy ra, hai tam giác A'B'C' và ABC đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh.
Xét tam giác OAB có A'B' // AB (định lí Thalès đảo) suy ra .
Tương tự, .
Vậy hai tam giác A'B'C' và ABC đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh với tỉ số .
Câu 10:
Cho điểm O nằm ngoài tam giác MNP. Trên các tia ON, OM, OP ta lần lượt lấy các điểm A, B, C sao cho .
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
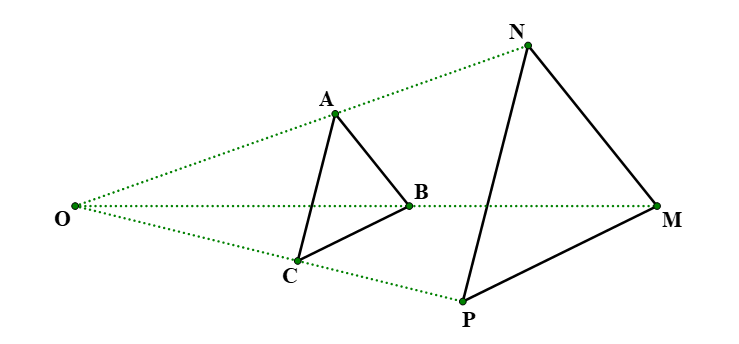
Ta có:
+ Ba đường thẳng NA, MB, PC cùng đi qua điểm O.
+ .
Suy ra, tam giác ABC đồng dạng phối cảnh với tam giác NMP và điểm O là tâm đồng dạng phối cảnh.
