10 câu hỏi trắc nghiệm thuộc Dạng 2. Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng

Trắc nghiệm Toán 8 Bài 36. Các trường hợp đồng dạng của hai tam giác vuông có đáp án

Dạng 2. Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng

124 lượt thi
10 câu hỏi
0 phút

Danh sách câu hỏi

Câu 1:

Bóng (AK) của một cột điện (MK) trên mặt đất dài 6 m. Cùng lúc đó một cột đèn giao thông (DE) cao 3 m có bóng (AE) dài 2 m. Tính chiều cao của cột điện (MK).

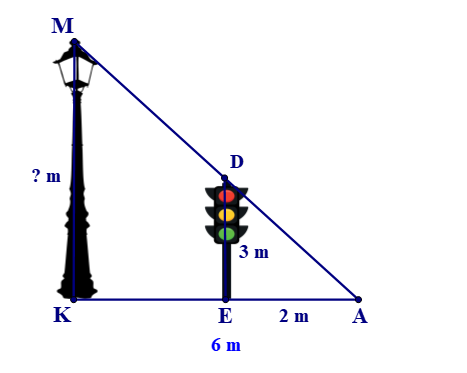
Bóng (AK) của một cột điện (MK) trên mặt đất dài 6 m. Cùng lúc đó một cột đèn giao thông (DE) cao 3 m (ảnh 1)

A. 3 m;

B. 6 m;

C. 9 m;

D. 12 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Xét tam giác DAE và tam giác MAK ta có:

$\hat{A E D} = \hat{A K M} = 90 °$

Góc A: chung

Do đó, $∆$ DAE ᔕ $∆$ MAK (g.g).

$\Rightarrow \frac{A E}{A K} = \frac{D E}{M K}$

$\Rightarrow M K = \frac{A K . D E}{A E} = \frac{6 . 3}{2} = 9 (m)$

Vậy chiều cao của cột điện là 9 m.

Câu 2:

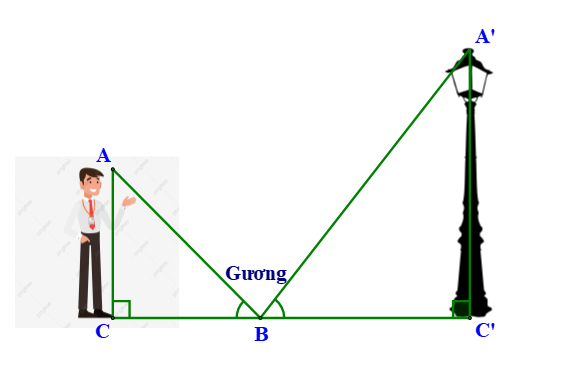
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét.

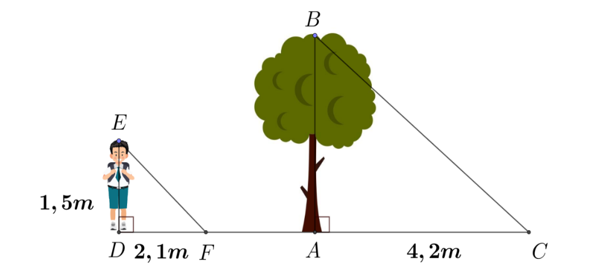
Nhận xét nào sau đây là đúng?

A. Chiều cao của cái cây là 2 m;

B. Chiều cao của cái cây là 3,5 m;

C. Chiều cao của cái cây là 3 m;

D. Chiều cao của cái cây là 2,5 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Các tia sáng là song song nên BC // EF, suy ra $\hat{D F E} = \hat{A C B}$ (đồng vị).

Từ đó suy ra $∆$ ABC ᔕ $∆$ DEF (g.g).

$\Rightarrow \frac{A C}{D F} = \frac{A B}{D E}$

$\Rightarrow A B = \frac{A C . D E}{D F} = \frac{4, 2 . 1, 5}{2, 1} = 3 (m)$

Vậy chiều cao của cái cây là 3 m.

Câu 3:

Bạn Hoàng muốn đo chiều cao của một cây dừa mọc thẳng đứng trong sân, bạn dùng một cây cọc AB dài 1,5 m và chiều dài thân mình để đo. Bạn nằm cách gốc cây 3 m (tính từ chân của bạn) và bạn cắm cọc thẳng đứng dưới chân mình thì bạn thấy đỉnh thân cọc và đỉnh cây thẳng hàng với nhau. Em hãy giúp bạn tính chiều cao của cây dừa, biết bạn Hoàng cao 1,7 m.

Bạn Hoàng muốn đo chiều cao của một cây dừa mọc thẳng đứng trong sân, bạn dùng một cây cọc (ảnh 1)

A. 4,0 m;

B. 4,1 m;

C. 4,2 m;

D. 4,3 m.

Xem đáp án

Bạn Hoàng muốn đo chiều cao của một cây dừa mọc thẳng đứng trong sân, bạn dùng một cây cọc (ảnh 2)

Câu 4:

Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát di chuyển sao cho thấy được đỉnh ngọn đèn trong tấm gương và góc ABC bằng góc A'BC'. Cho chiều cao tính từ mắt của người quan sát đến mặt đất là AC = 1,6 m; khoảng cách từ gương đến chân người là BC = 0,8 m; khoảng cách từ gương đến chân cột đèn là BC' = 1,5 m. Tính chiều cao của cột đèn A'C'.

Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt (ảnh 1)

A. 2 m;

B. 2,5 m;

C. 3 m;

D. 3,5 m.

Xem đáp án

Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt (ảnh 2)

Câu 5:

Một cột đèn cao 7 m có bóng trên mặt đất dài 4 m. Gần đấy có một toà nhà cao tầng có bóng trên mặt đất là 80 m (như hình vẽ). Em hãy cho biết toà nhà có bao nhiêu tầng, biết rằng mỗi tầng cao 3,5 m.

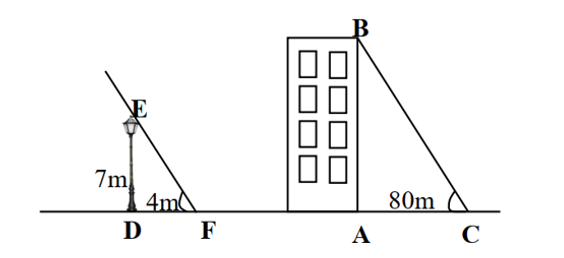
Một cột đèn cao 7 m có bóng trên mặt đất dài 4 m. Gần đấy có một toà nhà cao tầng có bóng trên mặt đất là (ảnh 1)

A. 40 tầng;

B. 45 tầng;

C. 30 tầng;

D. 20 tầng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét $∆$ ABC và $∆$ DEF ta có:

$\hat{E D F} = \hat{B A C} = 90 °$

$\hat{EF D} = \hat{B C A}$ (gt)

Do đó, $∆$ ABC ᔕ $∆$ DEF (g.g).

$\Rightarrow \frac{A B}{D E} = \frac{A C}{D F}$

$\Rightarrow \frac{A B}{7} = \frac{80}{4} \Rightarrow A B = \frac{80.7}{4} = 140 (m)$

Toà nhà cao 140 m.

Số tầng của toà nhà là: 140 : 3,5 = 40 (tầng).

Câu 6:

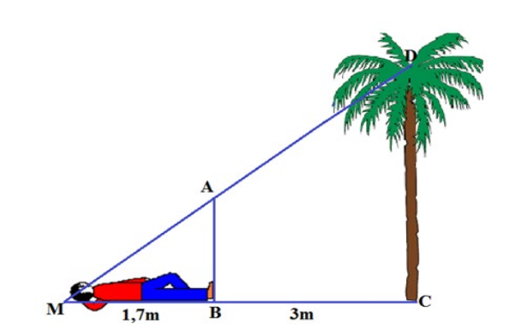
Một cột đèn cao 10 m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2 m và có bóng trải dài dưới mặt đất là 4,8 m. Tính chiều cao của cây xanh đó (làm tròn đến mét).

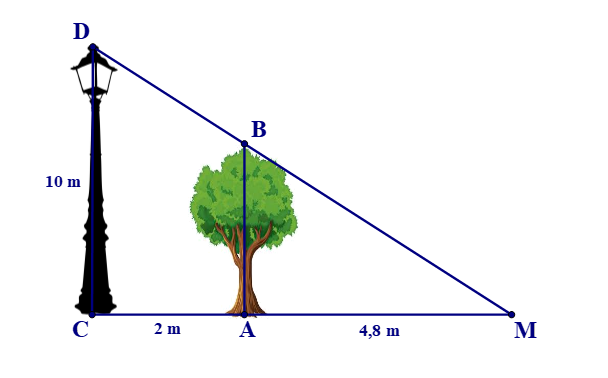
Một cột đèn cao 10 m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2 m và có bóng (ảnh 1)

A. 5 m;

B. 6 m;

C. 7 m;

D. 8 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

*) MC = MA + AC = 4,8 m + 2 m = 6,8 m.

Ta có: $\hat{M A B} = \hat{M C D} = 90 °$ và góc M chung. Suy ra $∆$ BMA ᔕ $∆$ DMC (g.g).

$\Rightarrow \frac{B A}{D C} = \frac{M A}{M C}$

$\Rightarrow \frac{A B}{10} = \frac{4, 8}{6, 8} \Rightarrow A B = \frac{10 . 4, 8}{6, 8} \approx 7 m$

Vậy chiều cao của cây xanh đó là 7 m.

Câu 7:

Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc CD đặt cố định vuông góc với mặt đất, với CD = 3 m và CA = 5 m. Sau đó, các bạn đã phối hợp để tìm được điểm E trên mặt đất là giao điểm của hai tia BD, AC và đo được CE = 2,5 m.

Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc (ảnh 1)

Tính chiều cao AB của bức tường.

A. 8 m;

B. 9 m;

C. 10 m;

D. 8,5 m.

Xem đáp án

Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc (ảnh 2)

Câu 8:

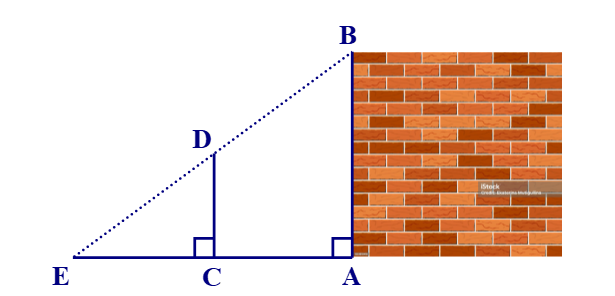
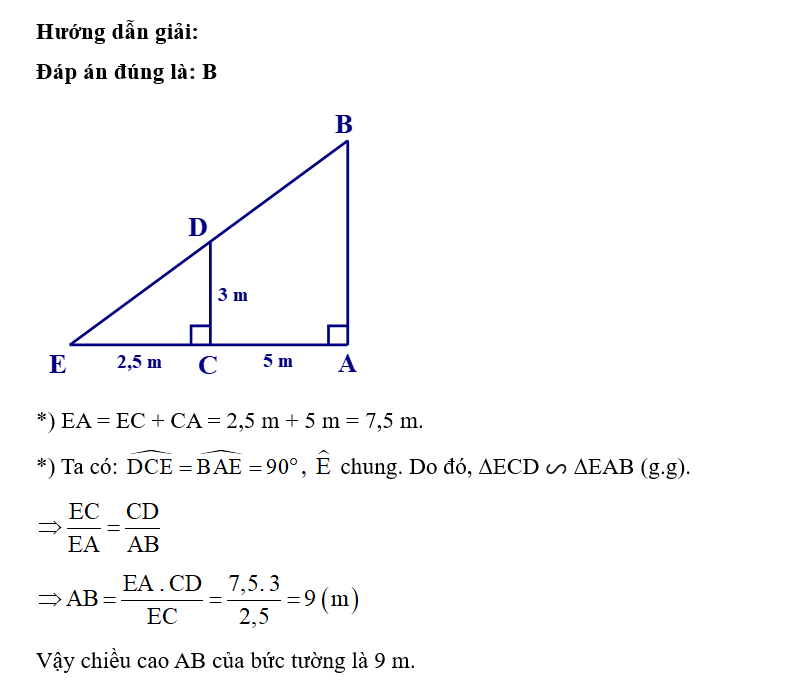
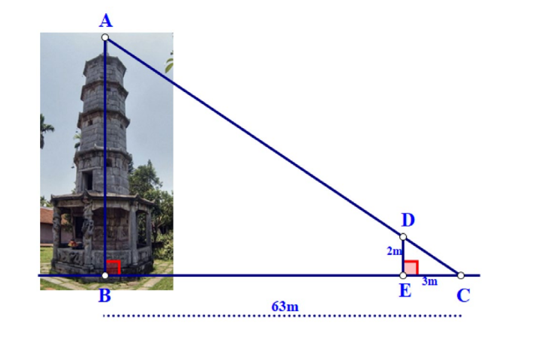
Bóng của một tháp trên mặt đất có độ dài BC = 63 m. Cùng thời điểm đó, một cây cột DE cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m. Tính chiều cao của tháp.

Bóng của một tháp trên mặt đất có độ dài BC = 63 m. Cùng thời điểm đó, một cây cột DE cao 2 m cắm vuông góc (ảnh 1)

A. 18 m;

B. 44 m;

C. 46 m;

D. 42 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có: $\hat{A B C} = \hat{D E C} = 90 °$ , góc C chung. Do đó, $∆$ ACB ᔕ $∆$ DCE (g.g).

$\Rightarrow \frac{D E}{A B} = \frac{E C}{B C}$

$\Rightarrow A B = \frac{D E . B C}{E C} = \frac{2 . 63}{3} = 42 (m)$

Vậy chiều cao của tháp là 42 m.

Câu 9:

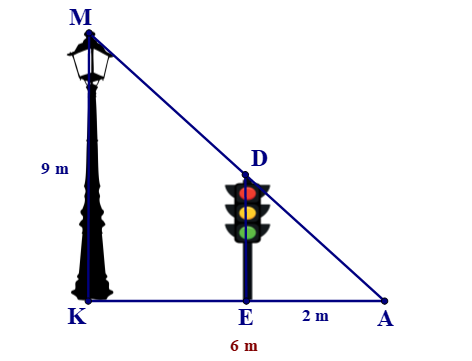
Bóng (AK) của một cột điện (MK) cao 9 m trên mặt đất dài 6 m. Cùng lúc đó một cột đèn (DE) có bóng (AE) dài 2 m. Tính chiều cao của một đèn giao thông (DE).

Bóng (AK) của một cột điện (MK) cao 9 m trên mặt đất dài 6 m. Cùng lúc đó một cột đèn (DE) có bóng (ảnh 1)

A. 1 m;

B. 2 m;

C. 3 m;

D. 4 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Xét tam giác DAE và tam giác MAK ta có:

$\hat{A E D} = \hat{A K M} = 90 °$

Góc A: chung

Do đó, $∆$ DAE ᔕ $∆$ MAK (g.g).

$\Rightarrow \frac{A K}{A E} = \frac{M K}{D E}$

$\Rightarrow D E = \frac{A E . M K}{A K} = \frac{2 .9}{6} = 3 (m)$

Vậy chiều cao của cột đèn giao thông DE là 3 m.

Câu 10:

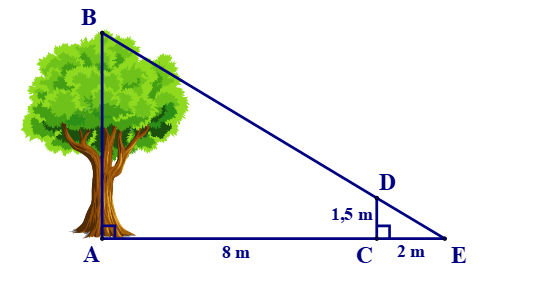
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2 m. Tính chiều cao của cây.

Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. (ảnh 1)

A. 7,5 m;

B. 15 m;

C. 30 m;

D. 12,5 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

+) AE = AC + CE = 8 m + 2 m = 10 m.

+) Ta có $\hat{B A E} = \hat{D C E} = 90 °$ , góc E chung.

Do đó, $∆$ DEC ᔕ $∆$ BEA (g.g).

$\Rightarrow \frac{D C}{A B} = \frac{E C}{E A}$

$\Rightarrow A B = \frac{D C . E A}{E C} = \frac{1, 5.10}{2} = 7, 5 (m)$

Vậy chiều cao của cây là 7,5 m.

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 36. Các trường hợp đồng dạng của hai tam giác vuông có đáp án

Dạng 2. Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương