10 câu hỏi trắc nghiệm thuộc Dạng 2. Trường hợp đồng dạng đặc biệt của hai tam giác

Trắc nghiệm Toán 8 Bài 33. Hai tam giác đồng dạng có đáp án

Dạng 2. Trường hợp đồng dạng đặc biệt của hai tam giác

112 lượt thi
10 câu hỏi
0 phút

Danh sách câu hỏi

Câu 1:

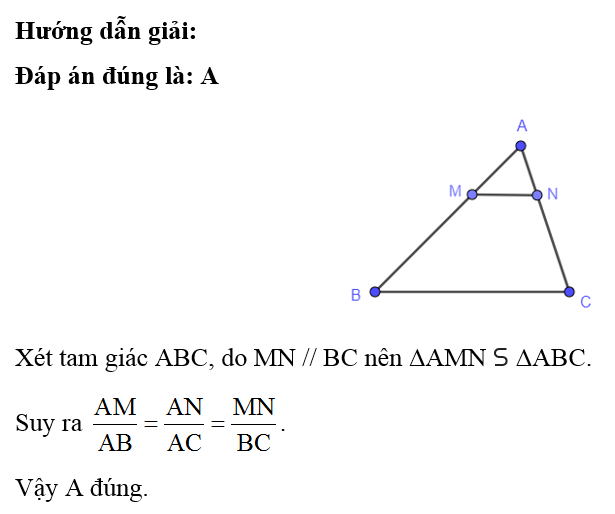
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?

A. 4;

B. 6;

C. 8;

D. 10.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

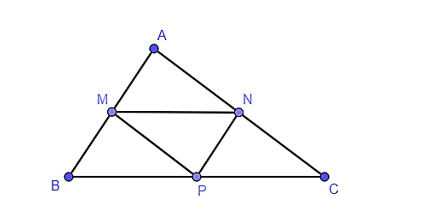
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam (ảnh 1)

Vì M, N lần lượt là trung điểm của AB, AC.

Suy ra MN là đường trung bình của tam giác ABC nên MN // BC.

Vì M, P lần lượt là trung điểm của AB, BC.

Suy ra MP là đường trung bình của tam giác ABC nên MP // AC.

Vì N, P lần lượt là trung điểm của AC, BC.

Suy ra NP là đường trung bình của tam giác ABC nên NP // AB.

Xét tam giác ABC:

+ Do MN // BC nên ΔAMN ᔕ ΔABC.

+ Do MP // AC nên ΔMBP ᔕ ΔABC.

+ Do NP // AB nên ΔNPC ᔕ ΔABC.

Vì ΔAMN ᔕ ΔABC, ΔMBP ᔕ ΔABC, ΔNPC ᔕ ΔABC nên các tam giác AMN, MBP, NPC đôi một đồng dạng với nhau.

Xét hai tam giác AMN và PNM có:

AM = PN $= \frac{1}{2} AB$

MN: Cạnh chung

MP = AN $= \frac{1}{2} AC$

Suy ra ΔAMN = ΔPNM (c – c – c).

Do đó, ΔAMN ᔕ ΔPNM.

Từ đó suy ra 5 tam giác AMN, PNM, MBP, NPC, ABC đôi một đồng dạng với nhau.

Vậy có tất cả 10 cặp tam giác đồng dạng.

Câu 2:

Cho hình vẽ sau biết MN // AB. Khẳng định nào sau đây là sai?

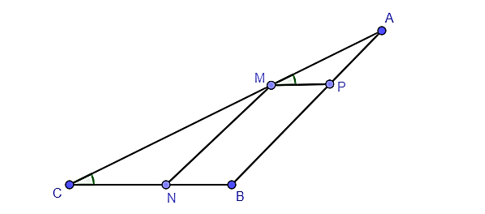
Cho hình vẽ sau biết MN song song AB. Khẳng định nào sau đây là sai? (ảnh 1)

A. ΔAMP ᔕ ΔACB;

B. ΔMCN ᔕ ΔACB;

C. ΔAMP ᔕ ΔMCN;

D. Cả A, B, C đều sai.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Xét tam giác ABC, do MN // AB nên ΔMCN ᔕ ΔACB.

Lại có $\hat{AMP} = \hat{ACB}$ mà hai góc này ở vị trí đồng vị nên MP // CB.

Xét tam giác ABC, do MP // CB nên ΔAMP ᔕ ΔACB.

Vì ΔMCN ᔕ ΔACB, ΔAMP ᔕ ΔACB nên ΔAMP ᔕ ΔMCN.

Vậy D sai.

Câu 3:

Cho hình vẽ, biết BE // AM // CF. Khi đó $\frac{1}{BE} + \frac{1}{CF}$ bằng

Cho hình vẽ, biết BE song song AM song song CF. Khi đó 1/ BE + 1/ CF bằng (ảnh 1)

A. $\frac{1}{AM}$ ;

B. $\frac{1}{B C}$ ;

C. $\frac{2}{AM}$ ;

D. $\frac{2}{B C}$

Xem đáp án

Cho hình vẽ, biết BE song song AM song song CF. Khi đó 1/ BE + 1/ CF bằng (ảnh 2)

Câu 4:

Cho hình dưới đây, khi đó độ dài cạnh AC

A. 3;

B. $\frac{4}{3}$ ;

C. 12;

\frac{16}{3}

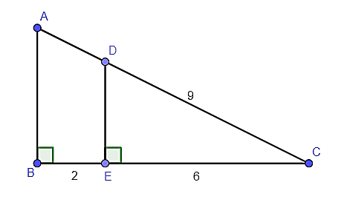
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

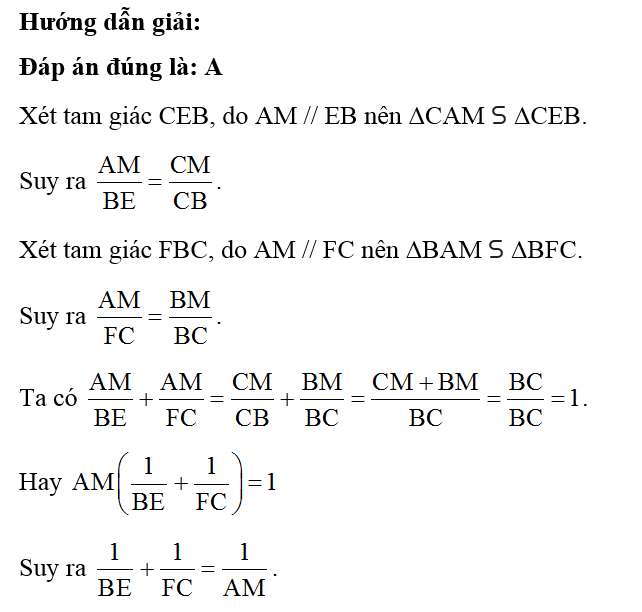
Có BC = CE + EB = 6 + 2 = 8.

Ta có DE ⊥ BC, AB ⊥ BC nên DE // AB.

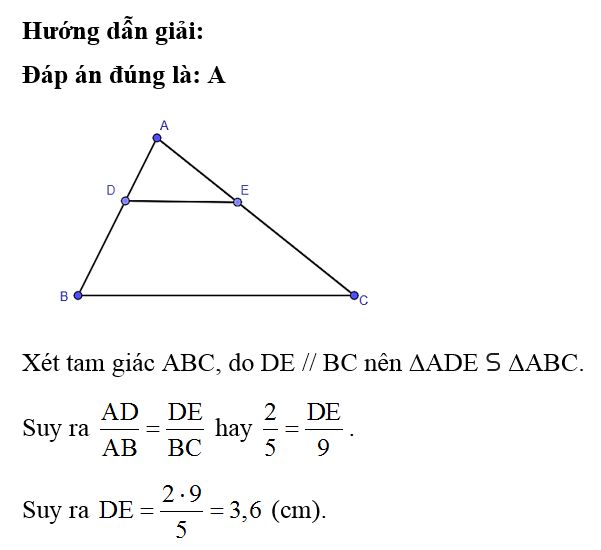
Xét tam giác ABC, do DE // AB nên ΔCDE ᔕ ΔCAB.

Suy ra $\frac{CD}{CA} = \frac{CE}{CB}$ hay $\frac{9}{CA} = \frac{6}{8}$ .

Suy ra $CA = \frac{9 \cdot 8}{6} = 12$ .

Câu 5:

Cho tam giác ABC và các điểm M, N lần lượt trên các cạnh AB, AC sao cho MN // BC. Khẳng định nào sau đây là đúng?

A. $\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}$ ;

B. $\frac{AM}{AB} = \frac{AC}{AN} = \frac{MN}{BC}$ ;

C. $\frac{AB}{AM} = \frac{AC}{AN} = \frac{MN}{BC}$ ;

\frac{AM}{AB} = \frac{AN}{AC} = \frac{BC}{MN}

Xem đáp án

Cho tam giác ABC và các điểm M, N lần lượt trên các cạnh AB, AC sao cho MN song song BC. Khẳng định nào sau đây là đúng? (ảnh 1)

Câu 6:

Cho hình sau, hãy chỉ ra hai tam giác đồng dạng và tỉ số đồng dạng của hai tam giác đó.

A. ΔCAB ᔕ ΔCDE với tỉ số đồng dạng $k = \frac{CA}{CD}$ ;

B. ΔABC ᔕ ΔDEC với tỉ số đồng dạng $k = \frac{AB}{DE}$ ;

C. ΔDEC ᔕ ΔBAC với tỉ số đồng dạng $k = \frac{BC}{DC}$ ;

D. ΔDEC ᔕ ΔBAC với tỉ số đồng dạng

k = \frac{DE}{BA}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

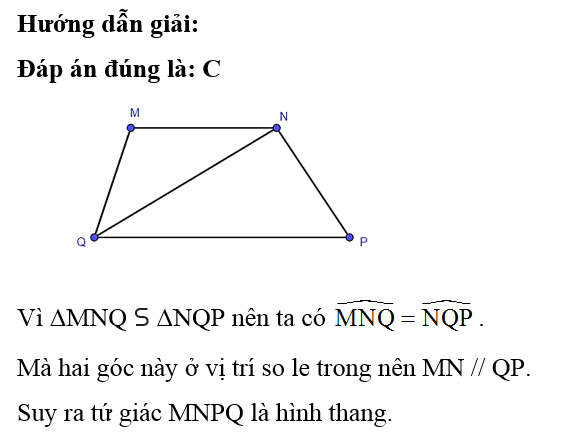
Ta có $\hat{BAC} = \hat{CED}$ mà hai góc này ở vị trí so le trong.

Suy ra AB // DE.

Xét tam giác ABC, do AB // DE nên ΔDEC ᔕ ΔBAC với tỉ số đồng dạng $k = \frac{DE}{BA}$ .

Câu 7:

Cho hình bình hành ABCD. Lấy E trên cạnh BC, tia DE cắt AB tại F. Khi đó tam giác FBE đồng dạng với tam giác nào dưới đây?

A. Tam giác FAD;

B. Tam giác DCE;

C. Cả A, B đều sai;

D. Cả A, B đều đúng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

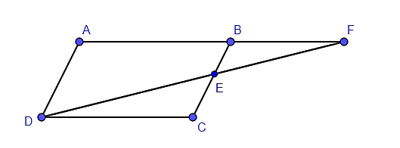
Cho hình bình hành ABCD. Lấy E trên cạnh BC, tia DE cắt AB tại F. Khi đó tam giác FBE đồng dạng với tam giác nào dưới đây? (ảnh 1)

Vì ABCD là hình bình hành nên AB // CD và AD // BC.

Xét tam giác FAD, do BE // AD (E ∈ BC, AD // BC) nên ΔFBE ᔕ ΔFAD.

Xét tam giác DEC, do BF // DC (AB // CD) nên ΔFBE ᔕ ΔDCE.

Vậy ΔFBE ᔕ ΔFAD và ΔFBE ᔕ ΔDCE.

Câu 8:

Nếu tam giác MNQ có HK // MN (H ∈ NQ, K ∈ MQ) thì

A. ΔKQH ᔕ ΔNQM;

B. ΔKQH ᔕ ΔMQN;

C. ΔMNQ ᔕ ΔHKQ;

D. ΔMNQ ᔕ ΔQKH.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

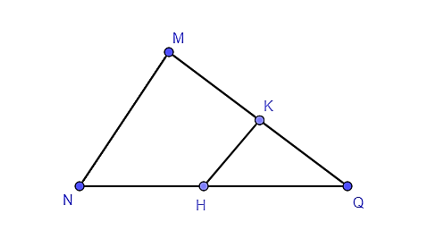
Nếu tam giác MNQ có HK song song MN (H thuộc NQ, K thuộc MQ) thì (ảnh 1)

Xét tam giác MNQ, do HK // MN nên ΔKQH ᔕ ΔMQN.

Câu 9:

Cho tứ giác MNPQ. Đường chéo NQ chia tứ giác thành hai tam giác đồng dạng với nhau là ΔMNQ và ΔNQP. Khẳng định nào sau đây là đúng?

A. MNPQ là hình chữ nhật;

B. MNPQ là hình bình hành;

C. MNPQ là hình thang;

D. MNPQ là hình vuông.

Xem đáp án

Cho tứ giác MNPQ. Đường chéo NQ chia tứ giác thành hai tam giác đồng dạng với nhau là ΔMNQ và ΔNQP. Khẳng định nào sau đây là đúng? (ảnh 1)

Câu 10:

Cho tam giác ABC, DE // BC (D ∈ AB, E ∈ AC). Biết AB = 5 cm, BC = 9 cm, AD = 2 cm, độ dài của ED là:

A. 3,6 cm;

B. 22,5 cm;

C. 1,1 cm;

D. 5,5 cm.

Xem đáp án

Cho tam giác ABC, DE // BC (D ∈ AB, E ∈ AC). Biết AB = 5 cm, BC = 9 cm, AD = 2 cm, độ dài của ED là: A. 3,6 cm (ảnh 1)

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 33. Hai tam giác đồng dạng có đáp án

Dạng 2. Trường hợp đồng dạng đặc biệt của hai tam giác

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương