Trắc nghiệm Toán 7 CTST Bài 4. Đường vuông góc và đường xiên có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 4. Đường vuông góc và đường xiên có đáp án (Phần 2) (Thông hiểu)
-
341 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có \(\widehat A = 80^\circ \) và \(\widehat B = 60^\circ .\) Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có: BC là cạnh đối diện của \(\widehat {\rm{A}}\) (1)
AC là cạnh đối diện của \(\widehat {\rm{B}}\) (2)
Vì 80° > 60° nên \(\widehat {\rm{A}} > \widehat {\rm{B}}\) (3)
Từ (1); (2) và (3) suy ra BC > AC (quan hệ giữa cạnh và góc trong tam giác).
Vậy ta chọn phương án D.
Câu 2:
Cho tam giác DEF có \(\widehat D = 38^\circ \) và \(\widehat E = 110^\circ .\) Độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét ∆DEF có: \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(38^\circ + 110^\circ + \widehat {\rm{F}} = 180^\circ \)
Suy ra \(\widehat {\rm{F}} = 180^\circ - 110^\circ - 38^\circ = 32^\circ \)
Vì \(32^\circ < 38^\circ < 110^\circ \) suy ra \(\widehat {\rm{F}} < \widehat {\rm{D}} < \widehat {\rm{E}}\) (1)
Ta lại có DE; EF; DF lần lượt là các cạnh đối diện của \(\widehat {\rm{F}};{\rm{ }}\widehat {\rm{D}};{\rm{ }}\widehat {\rm{E}}\) (2)
Từ (1) và (2) suy ra DE < EF < DF (quan hệ giữa cạnh và góc trong một tam giác).
Do đó độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là: DE; EF; DF.
Vậy ta chọn phương án A.
Câu 3:
Cho tam giác ABC có AB = 5 cm, BC = 9 cm và CA = 13 cm. Sắp xếp các góc của ∆ABC theo thứ tự giảm dần, ta có khẳng định đúng là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có \(\widehat {\rm{A}};{\rm{ }}\widehat {\rm{B}};{\rm{ }}\widehat {\rm{C}}\) lần lượt là các góc đối diện của các cạnh BC; AC; AB.
Mà AB < BC < AC (do 5 cm < 9 cm < 13 cm).
Suy ra \(\widehat C < \widehat {\rm{A}} < \widehat B\) (quan hệ giữa cạnh và góc trong một tam giác).
Do đó các góc của ∆ABC sắp xếp theo thứ tự giảm dần là: \(\widehat {\rm{B}};{\rm{ }}\widehat {\rm{A}};{\rm{ }}\widehat {\rm{C}}\).
Vậy ta chọn phương án B.
Câu 4:
Cho ∆ABC cân tại A có BC = 9 cm; chu vi ∆ABC bằng 25 cm. Chọn khẳng định sai:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
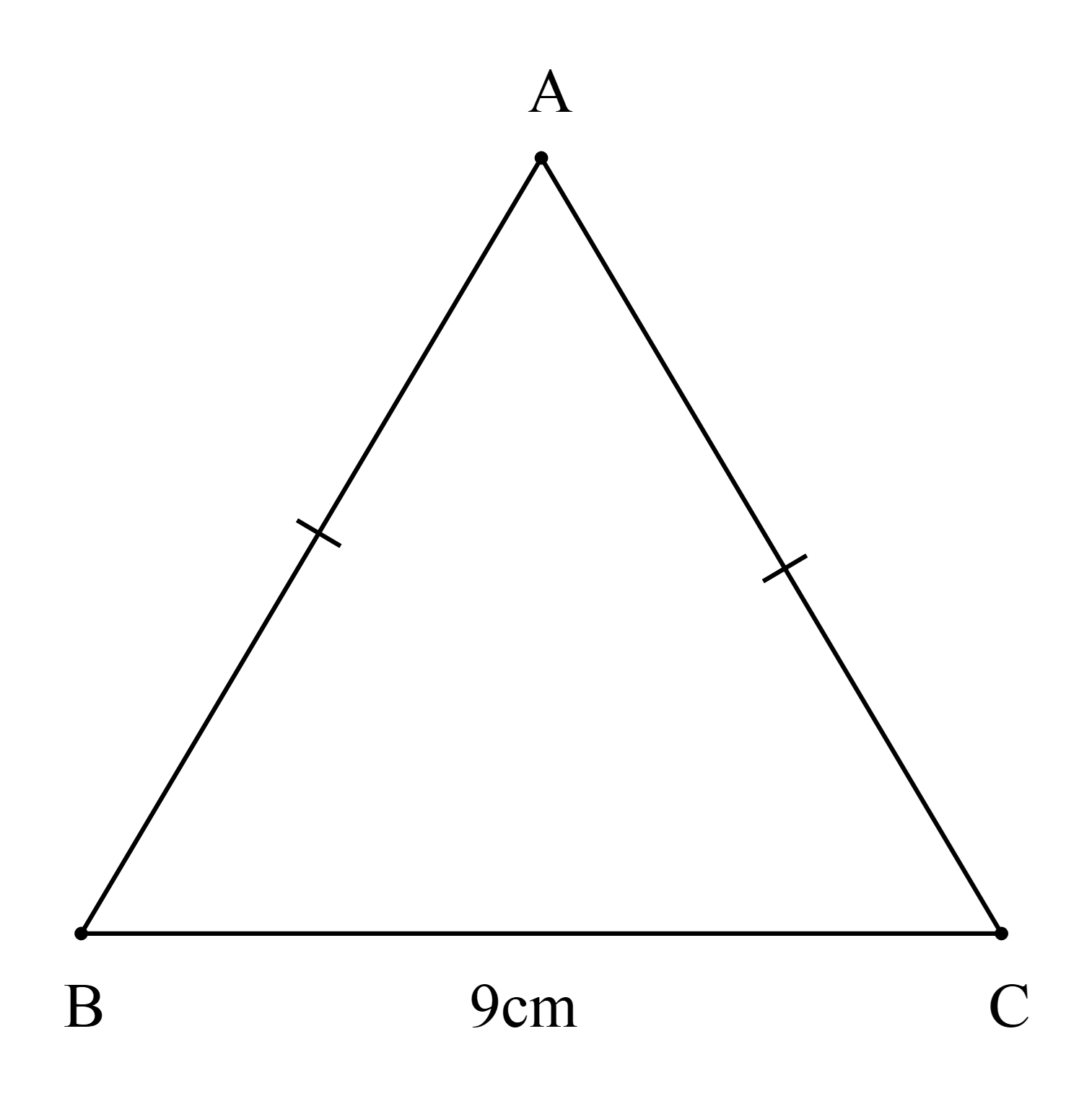
Do chu vi ∆ABC bằng 25 cm nên AB + AC + BC = 25 (cm).
Hay AB + AC + 9 = 25
Suy ra AB + AC = 25 – 9 = 16 (1)
Ta lại có AB = AC (do DABC cân tại A) (2)
Từ (1) và (2) suy ra AB = AC = \(\frac{{16}}{2} = 8\) (cm).
Ta có AB; AC; BC lần lượt là cạnh đối diện của \(\widehat {\rm{C}}{\rm{; }}\widehat {\rm{B}}{\rm{; }}\widehat {\rm{A}}\).
Mà DABC cân tại A suy ra \(\widehat {\rm{B}} = \widehat {\rm{C}}\), do đó C đúng.
AB < BC suy ra \(\widehat {\rm{C}} < \widehat {\rm{A}}\) (quan hệ giữa cạnh và góc trong tam giác), do đó D đúng, B sai
AC < BC suy ra \(\widehat {\rm{B}} < \widehat {\rm{A}}\)(quan hệ giữa cạnh và góc trong tam giác), do đó A đúng.
Vậy ta chọn phương án B.
Câu 5:
Cho hình vẽ
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì OB là đường vuông góc kẻ từ điểm O đến đường thẳng a;
OA, OC là các đường xiên kẻ từ O đến đường thẳng a.
Nên OB < OA; OB < OC (1)
Xét ∆OAC có \(\widehat {\rm{A}} > \widehat {\rm{C}}\) (vì 65° > 30°)
Suy ra: OC > OA (quan hệ giữa góc và cạnh đối diện trong tam giác) (2)
Từ (1) và (2) suy ra: OB < OA < OC.
Vậy ta chọn phương án A.
Câu 6:
Cho hình vẽ
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
• BO là đường xiên kẻ từ B đến Ox;
• BA là đường vuông góc kẻ từ B đến Ox.
Suy ra BA < BO (1)
Ta cũng có:
• BO là đường xiên kẻ từ B đến Oy;
• BC là đường vuông góc kẻ từ B đến Oy.
Suy ra BC < BO (2)
Từ (1) và (2) suy ra BA + BC < OB + OB.
Hay BA + BC < 2OB
Vậy ta chọn phương án A.
Câu 7:
Cho tam giác ABC có AH, BK, CL lần lượt là ba đường cao của tam giác ABC. Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
+) Ta có AH là đường vuông góc và AB là các đường xiên kẻ từ A đến BC.
Do đó AH < AB (1)
+) Ta có BK là đường vuông góc và BC là các đường xiên kẻ từ B tới AC.
Do đó BK < BC (2)
+) Ta có CL là đường vuông góc và CA là các đường xiên kẻ từ B tới AB.
Do đó CL < CA (3)
Từ (1) (2) và (3) suy ra:
AH + BK + CL < AB + BC + CA.
Vậy ta chọn phương án B.