Trắc nghiệm Toán 7 Bài 8. Tính chất ba đường cao của tam giác có đáp án
Trắc nghiệm Toán 7 Bài 8. Tính chất ba đường cao của tam giác có đáp án
-
157 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Điền vào chỗ trống sau: “Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là … của tam giác đó”.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.
Câu 2:
Điền vào chỗ trống sau: “Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này được gọi là … của tam giác”.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này được gọi là trực tâm của tam giác.
Câu 3:
Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
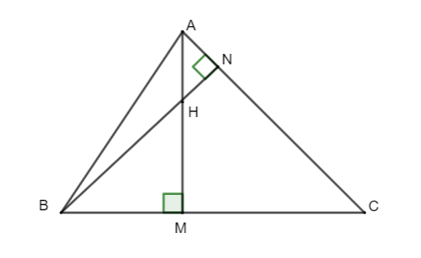
Vì hai đường cao AM và BN cắt nhau tại H nên H là trực tâm của ΔABC và CH là đường cao của ΔABC.
Do đó hai câu A và B đều đúng.
Câu 4:
Cho ΔABC có đường cao AM và BN cắt nhau tại H. Chọn câu đúng.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
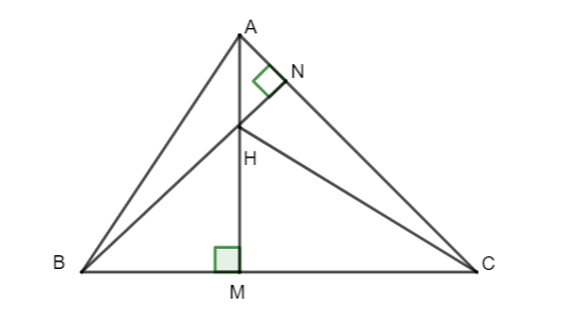
Xét ΔABC có:
AM là đường cao (gt);
BN là đường cao (gt);
AM và BN cắt nhau tại H.
Do đó H là trực tâm của ΔABC.
Suy ra CH là đường cao của ΔABC.
Vậy CH ⊥AB.
Câu 5:
Cho tam giác ABC vuông tại A. Lấy điểm O thuộc AB. Vẽ OM vuông góc với BC tại M. Tia MO cắt AC tại N. Chọn câu đúng.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
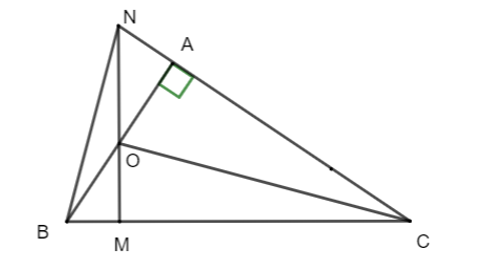
Xét ∆NBC có:
NM là đường cao (OM⊥BC, N Î OM);
BA là đường cao (BA ⊥ NC);
NM cắt BA tại O.
Do đó O là trực tâm của ∆ABC.
Suy ra CO là đường cao của ∆ABC.
Do vậy CO vuông góc với NB.
Vậy đáp án B và C đều đúng.
Câu 6:
Cho tam giác ABC có đường cao BE và trực tâm O .AO cắt BC tại H. Số đo ^AHC là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
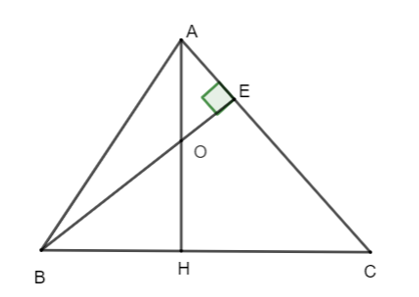
Xét ∆ABC có:
BE là đường cao (gt);
O là trực tâm (gt)
AH cắt BE tại O (gt).
Do đó AH là đường cao của ∆ABC.
Suy ra AH ⊥BC.
Vậy ^AHC = 90°.
Câu 7:
Cho tam giác ABC có đường cao AH và BE cắt nhau tại O. Cho ^ACH = 50°. Số đo góc ^BOH bằng :
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có: ^OBH + ^ECB = 90°.
Suy ra ^OBH = 90° − ^ECB = 90° − 50° = 40°.
Ta có: ^OBH + = 90°.
Suy ra ^BOH = 90° − ^OBH= 90° − 40° = 50°.
Vậy ^BOH = 50°.
Câu 8:
Cho tam giác ABC có đường cao AH và BE cắt nhau tại O. Cho ^OAE = 30°. Số đo ^BOH bằng :
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
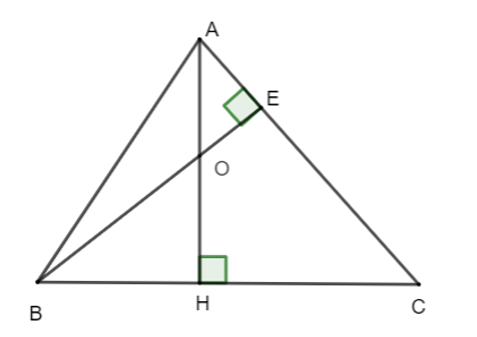
Ta có : ^OAE +^AOE = 90°
Suy ra ^AOE = 90° − ^OAE = 90° − 30° = 60°
Mà ^BOH =^AOE
Nên ^BOH = 60°.
Câu 9:
Vị trí trực tâm của tam giác tù:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vị trí trực tâm của tam giác tù nằm bên ngoài tam giác.
Câu 10:
Vị trí trực tâm của tam giác vuông:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Vị trí trực tâm của tam giác tù nằm trùng với đỉnh góc vuông.
Câu 11:
Cho tam giác ABC nhọn có ba đường cao AM, BN, CP. Biết AM = BN = CP. Khi đó tam giác ABC là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
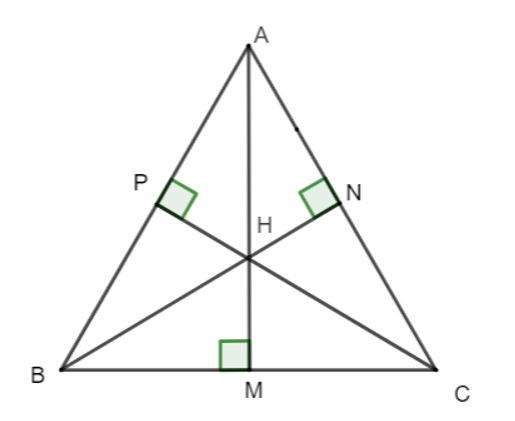
Gọi H là giao điểm của ba đường cao.
Ta có: ^PAH + ^PHA = 90°;
^MHC+ ^HCM = 90°;
^PHA = ^MHC (hai góc đối đỉnh).
Do đó ^PAH= ^HCM .
Xét ∆ABM vuông tại M và ∆CBP vuông tại P ta có:
^PAH = ^HCM (cmt).
AM = CP (gt).
Do đó ∆ABM = ∆CBP (cạnh góc vuông - góc nhọn).
Suy ra AB = BC (hai cạnh tương ứng) (1)
Chứng minh tương tự ta được ∆BNC = ∆AMC (cạnh góc vuông - góc nhọn)
Suy ra BC = AC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AB = BC = AC.
Vậy ∆ABC là tam giác đều.
Câu 12:
Tam giác nhọn có trực tâm:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tam giác nhọn có trực tâm nằm bên trong của tam giác.
Câu 13:
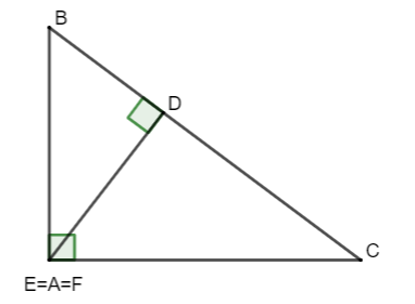
Cho ΔABC vuông cân tại B. Trên cạnh AB lấy điểm H. Trên tia đối của tia BC lấy điểm D sao cho BH = BD. Chọn câu đúng.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
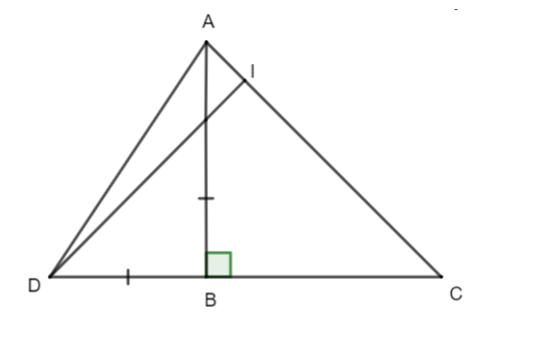
Gọi I là giao điểm của DH và AC.
Ta có: ∆ABC vuông cân tại B (gt).
Suy ra ˆC = 45°.
Xét ∆HBD có:
^HBD = 90°;
BH = BD (gt).
Do đó ∆HBD vuông cân tại B.
Suy ra ^BDH= 45° hay ^CDI = 45°.
Xét ∆DCI có:
ˆC = ^CDI = 45° (cmt)
Do đó ^DIC = 180° − (ˆC +^CDI ) = 180° − (45° + 45°) = 90°.
Vậy DH ⊥AC.
Câu 14:
Cho ∆ABC cân tại A có đường cao AK. Biết ^BAC= 40°. Số đo ^ACK bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
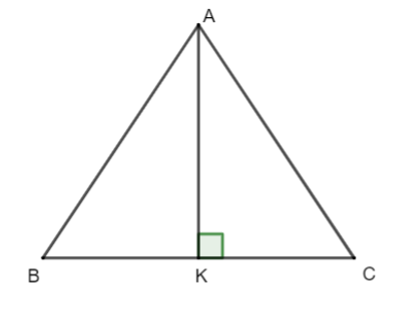
Xét ΔABK và ΔACK cùng vuông tại K có:
AK là cạnh chung;
AB = AC (vì ΔABC cân tại A).
Do đó ΔABK = ΔACK (cạnh huyền - cạnh góc vuông).
Suy ra ^KAC = ^BAK(hai cạnh tương ứng).
Do đó ^KAC =^BAK = ^BAC2 = 40o2 = 20°
Mà ^KAC + ^ACK = 90°.
Nên ^ACK = 90° − ^KAC = 90° − 20° = 70°
Vậy ^ACK = 70°.
Câu 15:
Ba đường cao của một tam giác tù:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ba đường cao của một tam giác tù đồng quy tại một điểm nằm ngoài tam giác.
