Trắc nghiệm Toán 7 Bài 2. Tia phân giác có đáp án (Vận dụng)
-
198 lượt thi
-
3 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ
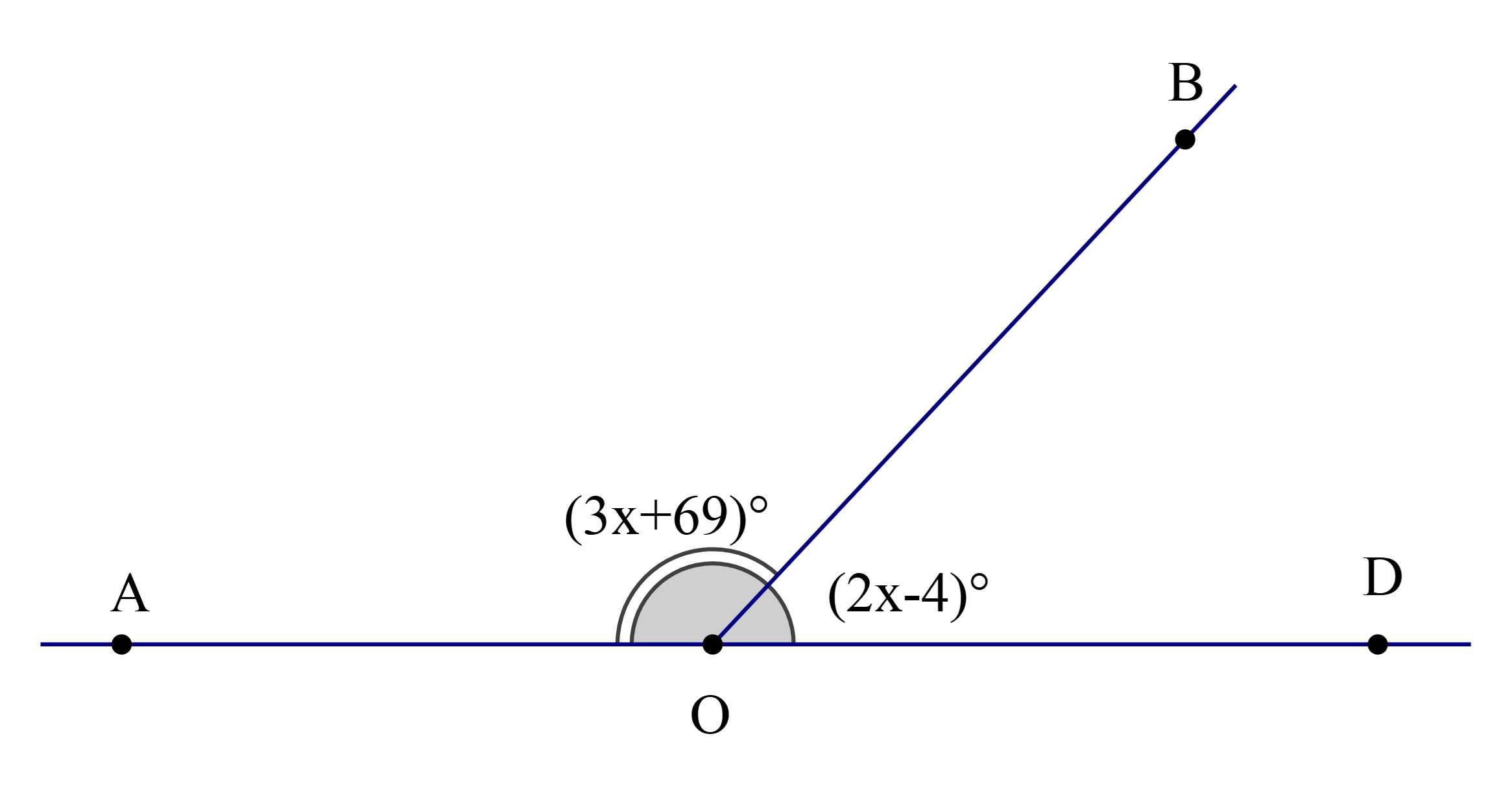
Kẻ OE là tia phân giác của \(\widehat {{\rm{BOD}}}\). Số đo của \(\widehat {{\rm{BOE }}}\)là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(\widehat {{\rm{AOB}}} + \widehat {{\rm{BOD}}} = 180^\circ \) (hai góc kề bù)
Nên (3x + 69)° + (2x – 4)° = 180°
Do đó (3x + 69 + 2x – 4)° = 180°
Suy ra 3x + 69 + 2x – 4 = 180
Hay 5x + 65 = 180
Suy ra 5x = 180 – 65 = 115
Suy ra x = 23.
Do đó \(\widehat {{\rm{BOD}}} = (2.23 - 4)^\circ = 42^\circ \)
Vì OE là tia phân giác của \(\widehat {{\rm{BOD}}}\)
Nên \(\widehat {{\rm{BOE}}} = \widehat {{\rm{EOD}}}\) (tính chất tia phân giác của một góc) (1)
Mà \(\widehat {{\rm{BOE}}} + \widehat {{\rm{EOD}}} = \widehat {{\rm{BOD}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra: \(\widehat {{\rm{BOE}}} = \frac{{\widehat {{\rm{BOD}}}}}{2} = \frac{{42^\circ }}{2} = 21^\circ \)
Vậy ta chọn phương án A.
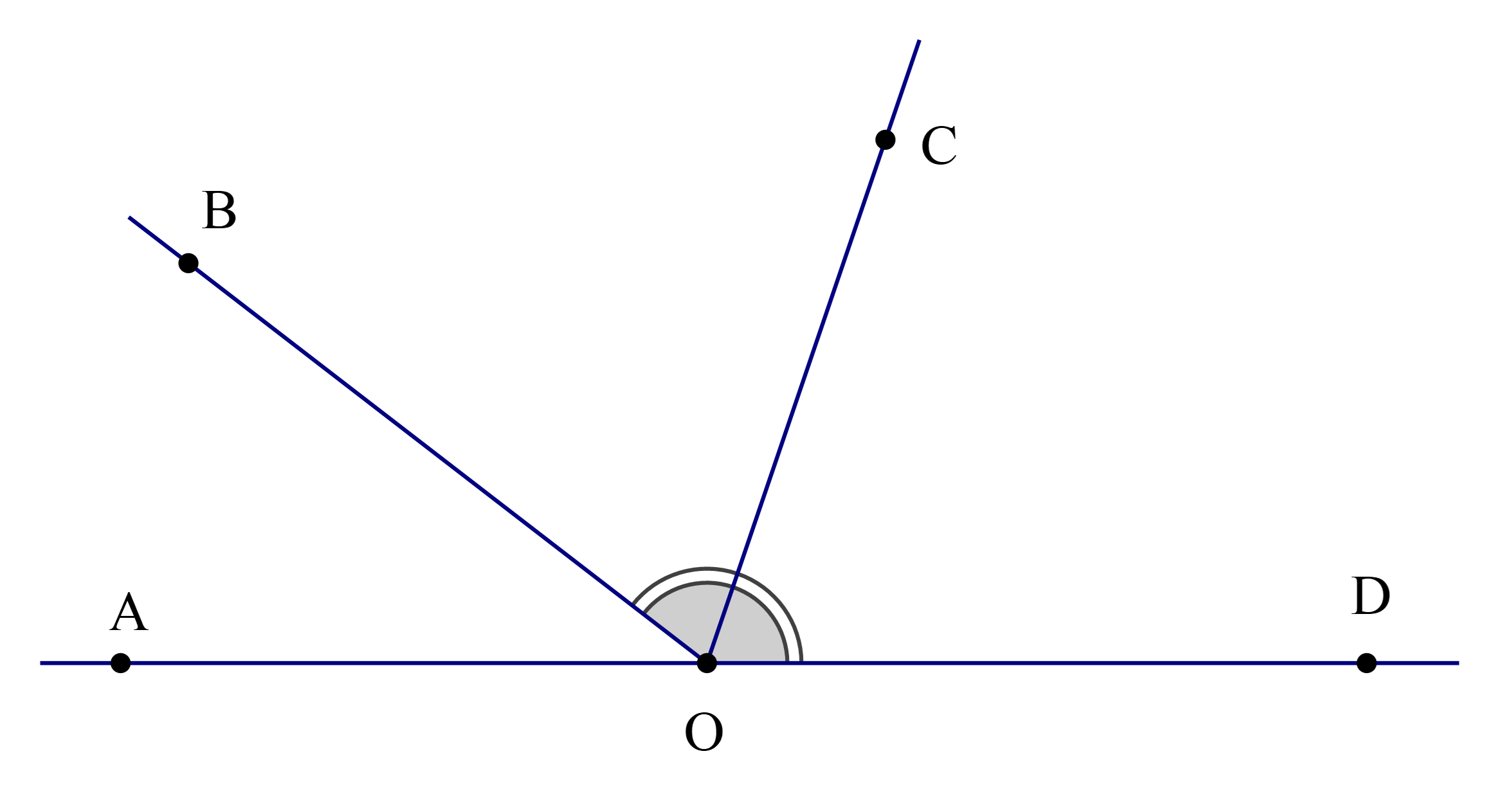
Câu 2:
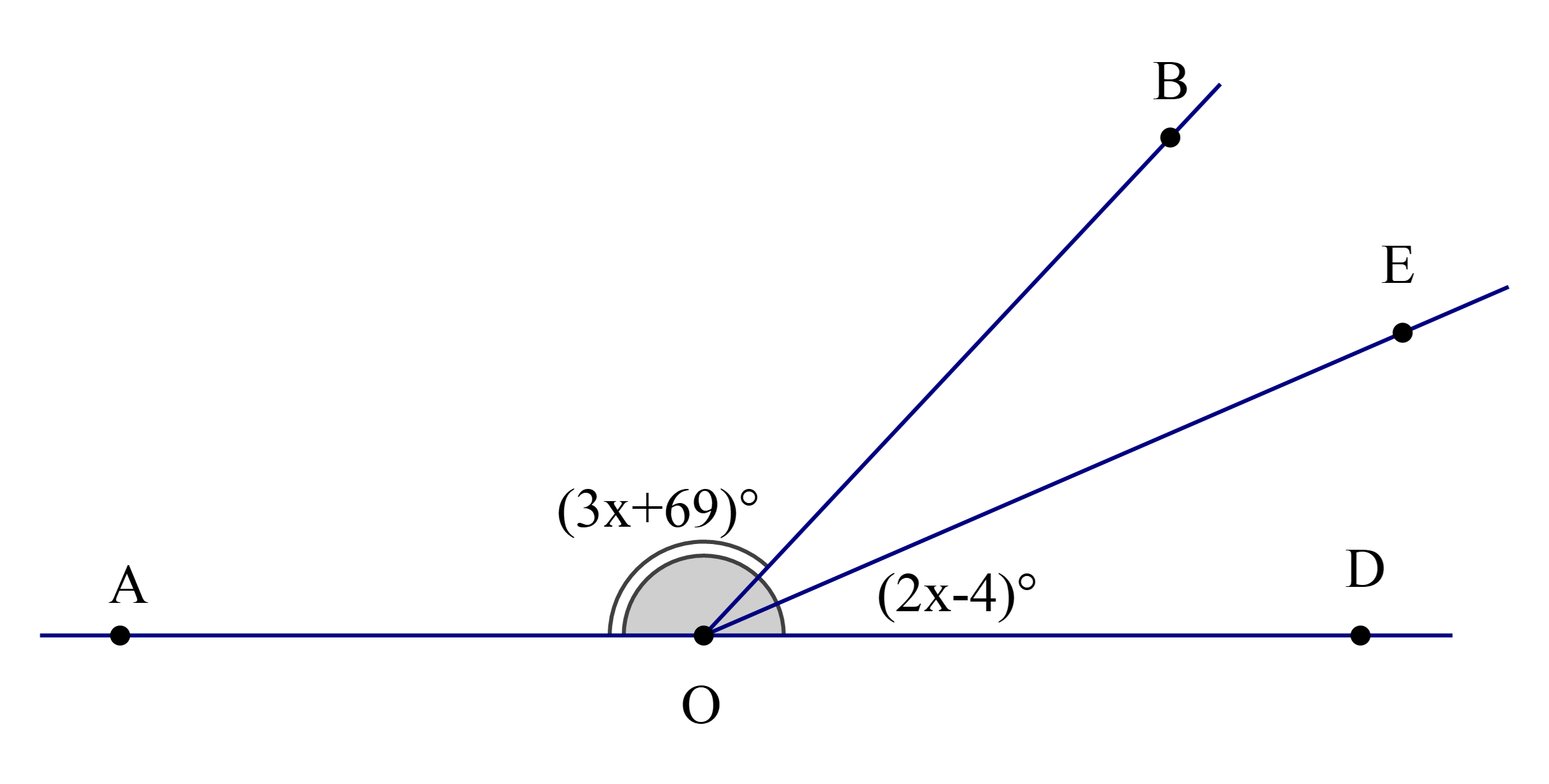
Cho hình vẽ, biết rằng OC là tia phân giác của \(\widehat {{\rm{BOD}}}\) và \(\widehat {{\rm{BOD}}} = 4\widehat {{\rm{AOB}}}\).
Số đo của \(\widehat {{\rm{COD}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\widehat {{\rm{AOB}}} + \widehat {{\rm{BOD}}} = 180^\circ \)(hai góc kề bù) (1)
Mà \(\widehat {{\rm{BOD}}} = 4\widehat {{\rm{AOB}}}\) (giả thiết) (2)
Thay (2) vào (1) ta có: \(\widehat {{\rm{AOB}}} + 4\widehat {{\rm{AOB}}} = 180^\circ \)
Hay \(5\widehat {{\rm{AOB}}} = 180^\circ \)
Do đó \(\widehat {{\rm{AOB}}} = \frac{{180^\circ }}{5} = 36^\circ \)
Thay \(\widehat {{\rm{AOB}}} = 36^\circ \) vào (2) ta có: \(\widehat {{\rm{BOD}}} = 4.36^\circ = 144^\circ \)
Theo bài tia OC là tia phân giác của \(\widehat {{\rm{BOD}}}\)
Do đó \(\widehat {{\rm{BOC}}} = \widehat {{\rm{COD}}}\) (tính chất tia phân giác của một góc) (3)
Mà \(\widehat {{\rm{BOC}}} + \widehat {{\rm{COD}}} = \widehat {{\rm{BOD}}}\) (hai góc kề nhau) (4)
Từ (3) và (4) suy ra \(\widehat {{\rm{BOC}}} = \widehat {{\rm{COD}}} = \frac{{\widehat {{\rm{BOD}}}}}{2} = \frac{{144^\circ }}{2} = 72^\circ \)
Vậy ta chọn phương án C.
Câu 3:
Cho hình vẽ, biết rằng Oz, Ot lần lượt là tia phân giác của \(\widehat {{\rm{yOu}}}\)và \(\widehat {{\rm{zOu}}}\) và \(\widehat {tOu} = a^\circ .\)
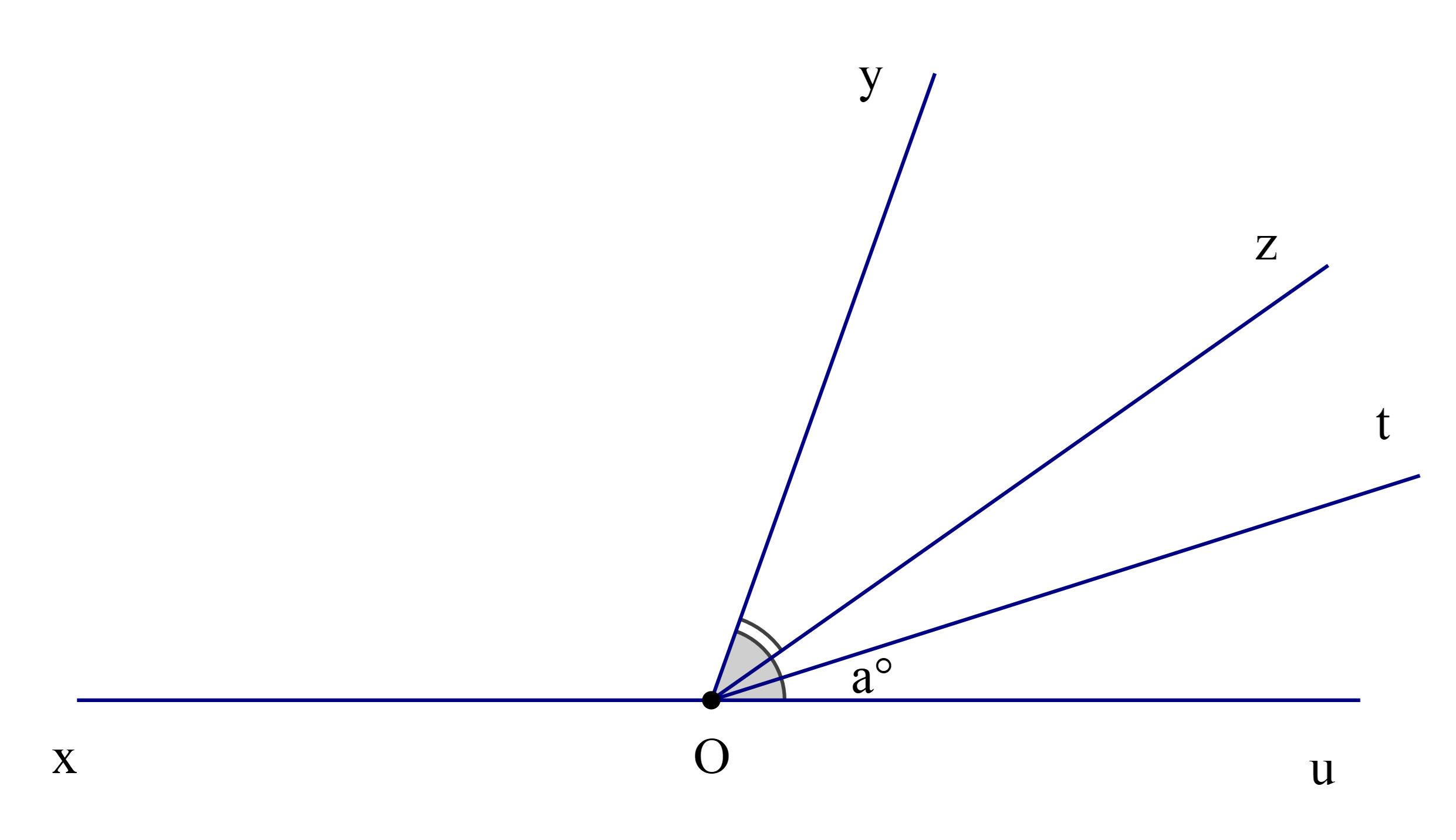
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Theo bài ra ta có Ot là tia phân giác của \(\widehat {zOu}\)
Suy ra \(\widehat {{\rm{zOt}}} = \widehat {{\rm{tOu}}} = a^\circ \) (tính chất tia phân giác của một góc) (1)
Mà \(\widehat {{\rm{zOt}}} + \widehat {{\rm{tOu}}} = \widehat {{\rm{zOu}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{zOt}}} = \widehat {{\rm{tOu}}} = \frac{{\widehat {{\rm{zOu}}}}}{2}\)
Do đó \(\widehat {zOu} = 2\widehat {{\rm{tOu}}} = 2a^\circ \)
Ta lại có Oz là tia phân giác của \(\widehat {{\rm{yOu}}}\)
Suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOu}}}\) (tính chất tia phân giác của một góc) (3)
Mà \(\widehat {{\rm{yOz}}} + \widehat {{\rm{zOu}}} = \widehat {{\rm{yOu}}}\) (hai góc kề nhau) (4)
Từ (3) và (4) suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOu}}} = \frac{{\widehat {{\rm{yOu}}}}}{2}\)
Do đó \(\widehat {{\rm{yOu}}} = 2\widehat {{\rm{zOu}}}\)
Mà \(\widehat {{\rm{zOu}}} = 2a^\circ \)
Do đó \(\widehat {{\rm{yOu}}} = 2\widehat {{\rm{zOu}}} = 2.2a^\circ = 4a^\circ \)
Ta có \(\widehat {{\rm{xOy}}} + \widehat {yOu} = 180^\circ \) (hai góc kề bù)
Hay \(\widehat {{\rm{xOy}}} = 180^\circ - \widehat {{\rm{yOu}}}\)
Suy ra \(\widehat {{\rm{xOy}}} = 180^\circ - 4a^\circ \)
Vậy ta chọn phương án D.
