Trắc nghiệm Toán 7 Bài 2. Số thực. Giá trị tuyệt đối của một số thực (Phần 2) có đáp án
Trắc nghiệm Toán 7 Bài 2. Số thực. Giá trị tuyệt đối của một số thực (Thông hiểu) có đáp án
-
225 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Nhận xét đúng về vị trí của các số thực 0; √3; 52 trên trục số là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có: 0<√3=1,732...<52=2.5
Do đó trên trục số:
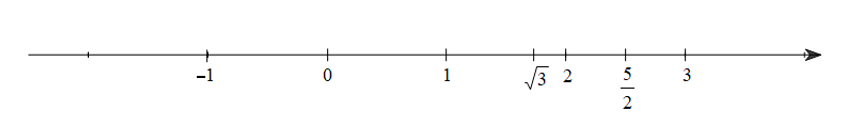
• Điểm √3 nằm bên trái điểm 52. Do đó A đúng và B sai.
• Điểm √3 nằm bên phải điểm 0. Do đó C sai.
• Điểm 0 nằm bên trái điểm 52. Do đó D sai.
Ta chọn phương án A.
Câu 2:
Số đối của các số thực 3; –π; √15 lần lượt là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Số đối của số 3 là –3;
Số đối của số –π là π;
Số đối của số √15 là số -√15
Vậy số đối của các số thực 3; –π; √15 lần lượt là: –3; π; -√15
Ta chọn phương án A.
Câu 3:
Giá trị của biểu thức: |–3,5| + |1,7| – 0,2 là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: |–3,5| + |1,7| – 0,2
= 3,5 + 1,7 – 0,2
= 5
Ta chọn phương án C.
Câu 4:
Có bao nhiêu số thực x thỏa mãn |x| = 2?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có |x| = 2
Suy ra x = 2 hoặc x = –2.
Vậy có hai số thực x thỏa mãn |x| = 2 là 2 và –2.
Ta chọn phương án B.
Câu 5:
Có bao nhiêu số thực x thỏa mãn |x|=−√3?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Do |x| luôn không âm mà −√3<0 nên không có số thực x nào thỏa mãn điều kiện đề bài.
Ta chọn phương án D.
Câu 6:
Chọn khẳng định đúng.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
• Ta có –0,6 < 0 nên |–0,6| = –(–0,6) = 0,6. Do đó phương án B sai.
• Vì –0,7 < 0 nên |–0,7| = –(–0,7) = 0,7.
Vì 0,6 < 0,7 nên |–0,6| < |–0,7|. Do đó phương án A sai.
• Vì √0,7 và -√0,7 là hai số đối nhau nên |√0,7|=|−√0,7|.
Do đó phương án C sai.
• Vì −23<0 nên |−23|=−(−23)=23;
Vì 13>0 nên |13|=13;
Vì 23>13 nên |−23|>|13|. Do đó phương án D đúng.
Vậy ta chọn phương án D.
Câu 7:
Tính √|−16| ta được kết quả là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có: √|−16|=√16=4
Ta chọn phương án B.