Trắc nghiệm Toán 7 Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án
Trắc nghiệm Toán 7 Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án
-
120 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Phát biểu đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Câu 2:
Cho tam giác ABC và tam giác MNP có \(\widehat A = \widehat P\); AC = MP, \[\widehat C = \widehat M\]. Phát biểu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét \[\Delta ACB\] và \[\Delta PMN\] có:
\(\widehat A = \widehat P\)
AC = MP
\[\widehat C = \widehat M\]
Suy ra \[\Delta ACB = \Delta PMN\] (g.c.g)
(Trong đó:
Đỉnh B tương ứng với đỉnh N.
Đỉnh C tương ứng với đỉnh M.
Đỉnh A tương ứng với đỉnh P)
Câu 3:
Cho tam giác ABC và tam giác MNP có \(\widehat A = \widehat P\); AB = PN, AC = PM. Phát biểu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét \[\Delta ABC\] và \[\Delta MNP\] có:
AB = PN
\(\widehat A = \widehat P\)
AC = PM
Suy ra \[\Delta ABC = \Delta PNM\] (c.g.c)
(Trong đó:
Đỉnh A tương ứng với đỉnh P.
Đỉnh B tương ứng với đỉnh N.
Đỉnh C tương ứng với đỉnh M)
Câu 4:
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat B = \widehat P\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp góc – cạnh – góc?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì: tam giác ABC và tam giác NPM có BC = PM; \(\widehat B = \widehat P\).
Nên: Để tam giác ABC bằng tam giác NPM theo trường hợp góc – cạnh – góc cần thêm điều kiện \[\widehat C = \widehat M\]. (Do \(\widehat B\) và \[\widehat C\] là hai góc kề cạnh BC và \(\widehat P\) và \[\widehat M\] là hai góc kề cạnh PM)
Câu 5:
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat B = \widehat P\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì: tam giác ABC và tam giác NPM có BC = PM; \(\widehat B = \widehat P\).
Nên: Để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh cần thêm điều kiện AB = NP. (Do \(\widehat B\) là góc xen giữa hai cạnh BC và AB; \(\widehat P\) là góc xen giữa hai cạnh PM và NP).
Câu 6:
Cho tam giác ABC và tam giác DEF có AB = DE, \(\widehat B = \widehat E,{\rm{ }}\widehat A = \widehat D\). Biết AC = 6 cm. Độ dài DF là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét \[\Delta ABC\] và \[\Delta DEF\] có:
\(\widehat A = \widehat D\)
AB = DE
\(\widehat B = \widehat E\)
⇒ \[\Delta ABC = \Delta DEF\] (g.c.g)
Suy ra: AC = DF (hai cạnh tương ứng)
Mà AC = 6 cm ⇒ DF = 6 cm
Câu 7:
Cho tam giác ABC và tam giác DEF có AB = DE, AC = DF, \(\widehat A = \widehat D\). Biết \(\widehat B = 60^\circ \). Số đo góc E là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét \[\Delta ABC\] và \[\Delta DEF\] có:
AB = DE
\(\widehat A = \widehat D\)
AC = DF
⇒ \[\Delta ABC = \Delta DEF\] (c.g.c)
Suy ra: \(\widehat B = \widehat E\) (hai góc tương ứng)
Mà \(\widehat B = 60^\circ \) ⇒ \(\widehat E = 60^\circ \)
Câu 8:
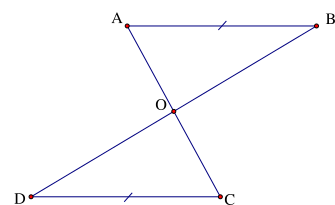
Cho hình vẽ sau, trong đó \(AB{\rm{//}}CD\), AB = CD. Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét \[\Delta AOB\] và \[\Delta COD\] có:
\(\widehat {OAB} = \widehat {OCD}\) (2 góc so le trong do \(AB{\rm{//}}CD\))
AB = CD (gt)
\(\widehat {OBA} = \widehat {ODC}\) (2 góc so le trong do \(AB{\rm{//}}CD\))
\[ \Rightarrow \Delta AOB = \Delta COD\] (g.c.g)
Suy ra OA = OC (hai cạnh tương ứng)
Câu 9:
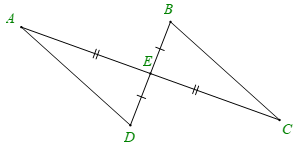
Cho hình vẽ dưới đây, biết AE = CE, DE = BE. Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hai tam giác AED và CEB có:
AE = CE
\(\widehat {AED} = \widehat {CEB}\) (hai góc đối đỉnh)
DE = BE
Do đó \(\Delta AED = \Delta CEB\) (c.g.c)
Câu 10:
Cho \[\Delta DEF\] có \(\widehat E = \widehat F\). Tia phân giác của góc D cắt EF tại I. Ta có
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
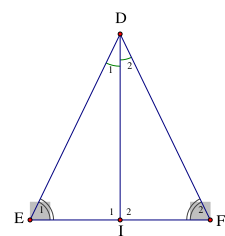
+ Xét \[\Delta DEI\] có:
\[\widehat {{D_1}} + \widehat {{E_1}} + \widehat {{I_1}} = {180^{\rm{o}}}\] (ĐL tổng ba góc của tam giác)
+ Xét \[\Delta DFI\] có:
\[\widehat {{D_2}} + \widehat {{F_2}} + \widehat {{I_2}} = {180^{\rm{o}}}\] (ĐL tổng ba góc của tam giác)
Mà: \(\widehat {{E_1}} = \widehat {{F_2}}\) (gt) và \(\widehat {{D_1}} = \widehat {{D_2}}\) (Vì DI là tia phân giác của góc \[D\])
Nên: \(\widehat {{I_1}} = \widehat {{I_2}}\) (Hay \[\widehat {DIE} = \widehat {DIF}\]) (A và D sai)
+ Xét \[\Delta DEI\] và \[\Delta DFI\], có:
\(\widehat {{D_1}} = \widehat {{D_2}}\) (cmt)
DI là cạnh chung
\(\widehat {{I_1}} = \widehat {{I_2}}\) (cmt)
\[ \Rightarrow \Delta DIE = \Delta DIF\] (g.c.g) (B sai)
Suy ra IE = IF; DE = DF (2 cạnh tương ứng)
Vậy C đúng.
Câu 11:
Cho hình vẽ dưới đây, biết CE = DE và \(\widehat {CEA} = \widehat {DEA}\).
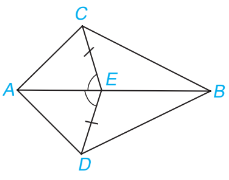
Khẳng định sai là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét \(\Delta AEC\) và \(\Delta AED\) có:
CE = DE (theo giả thiết)
\(\widehat {CEA} = \widehat {DEA}\) (theo giả thiết)
AE là cạnh chung
Do đó \(\Delta AEC = \Delta AED\) (c.g.c)
⇒ AC = AD (2 cạnh tương ứng) và \(\widehat {CAE} = \widehat {DAE}\) (2 góc tương ứng)
Xét \(\Delta ABC\) và \(\Delta ABD\) có:
AC = AD (chứng minh trên)
\(\widehat {CAE} = \widehat {DAE}\) (chứng minh trên)
AB là cạnh chung
Do đó \(\Delta ABC = \Delta ABD\) (c.g.c)
⇒ \(\widehat {ACB} = \widehat {ADB}\) (2 góc tương ứng)
Vậy khẳng định D sai.
Câu 12:
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm I tùy ý, qua I vẽ đường thẳng vuông góc với OI cắt Ox ở E và cắt Oy ở F. Trong các khẳng định sau, khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là:
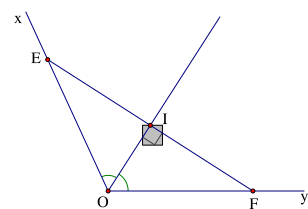
+ Xét \[\Delta OEI\] và \[\Delta OFI\] có:
\[\widehat {EOI} = \widehat {FOI}\] (Vì OI là tia phân giác của \[\widehat {xOy}\])
OI là cạnh chung
\[\widehat {OIE} = \widehat {OIF} = {90^{\rm{o}}}\] (\(OI \bot EF\))
\[ \Rightarrow \Delta OEI = \Delta OFI\] (g.c.g) (A sai)
Suy ra IE = IF, OE = OF (2 cạnh tương ứng). (B và C sai)
\[\widehat {IEO} = \widehat {IFO}\] (2 góc tương ứng)
Vậy D đúng.
Câu 13:
Cho hình vẽ dưới đây, biết đoạn thẳng JK song song và bằng đoạn thẳng ML.
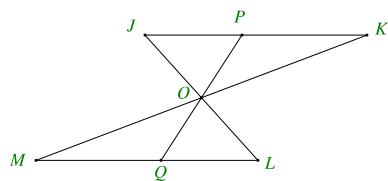
Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì JK ∥ ML nên:
\(\widehat {{\rm{OJ}}K} = \widehat {OLM}\) (2 góc so le trong)
\(\widehat {{\rm{O}}KJ} = \widehat {OML}\) (2 góc so le trong)
Xét \(\Delta {\rm{JO}}K\) và \(\Delta LOM\) có:
\(\widehat {{\rm{OJ}}K} = \widehat {OLM}\) (chứng minh trên)
JK = ML (theo giả thiết)
\(\widehat {{\rm{O}}KJ} = \widehat {OML}\) (chứng minh trên)
Do đó \(\Delta JOK = \Delta LOM\) (g.c.g)
⇒ KO = MO (2 cạnh tương ứng)
Xét \(\Delta KOP\) và \(\Delta MOQ\) có:
\(\widehat {{\rm{O}}KJ} = \widehat {OML}\) (chứng minh trên)
KO = MO (chứng minh trên)
\(\widehat {KOP} = \widehat {MOQ}\) (2 góc đối đỉnh)
Do đó \(\Delta KOP = \Delta MOQ\) (g.c.g)
⇒ OP = OQ (2 cạnh tương ứng).
Vậy khẳng định C đúng.
Câu 14:
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
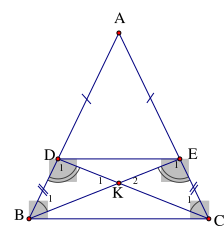
+ Có: AB = AC, AD = AE (gt)
AB = AD + DB, AC = AE + EC
Suy ra: DB = EC (A đúng)
+ Xét \[\Delta ABE\] và \[\Delta ACD\] có:
AB = AC (gt)
\[\widehat {BAC}\] là góc chung
AE = AD (gt)
\[\Delta ABE = \Delta ACD\] (c.g.c)
⇒ BE = CD (2 cạnh tương ứng) (B đúng)
và \(\widehat {{B_1}} = \widehat {{C_1}}\); \(\widehat {AEB} = \widehat {ADC}\) (2 góc tương ứng)
+ Có \[\widehat {ADC} + \widehat {{D_1}} = {180^{\rm{o}}}\] (2 góc kề bù)
\[\widehat {AEB} + \widehat {{E_1}} = {180^{\rm{o}}}\] (2 góc kề bù)
Mà \(\widehat {AEB} = \widehat {ADC}\) (cmt) ⇒ \(\widehat {{D_1}} = \widehat {{E_1}}\)
Xét \[\Delta BDK\] và \[\Delta CEK\] có:
\(\widehat {{B_1}} = \widehat {{C_1}}\) (cmt)
DB = EC (cmt)
\(\widehat {{D_1}} = \widehat {{E_1}}\) (cmt)
\[ \Rightarrow \Delta BDK = \Delta CEK\] (g.c.g)
Suy ra \[BK = KC\] (C đúng; D sai)
Câu 15:
Cho tứ giác ABCD, \[AB{\rm{//}}DC\], \[AD{\rm{//}}BC\], O là giao của AC và BD. Câu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
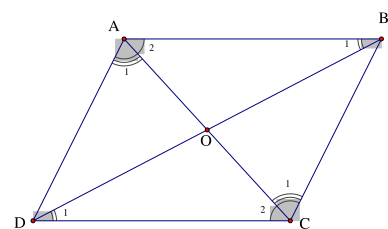
+ Vì
\[AB{\rm{//}}DC\] nên \[\widehat {{A_2}} = \widehat {{C_2}}\]; \[\widehat {{B_1}} = \widehat {{D_1}}\] (2 góc so le trong)
+ Vì \[AD{\rm{//}}BC\] nên \[\widehat {{A_1}} = \widehat {{C_1}}\] (2 góc so le trong)
+ Xét \[\Delta ABC\] và \[\Delta CDA\] có:
\[\widehat {{A_2}} = \widehat {{C_2}}\] (cmt)
AC là cạnh chung
\[\widehat {{C_1}} = \widehat {{A_1}}\] (cmt)
\[ \Rightarrow \Delta ABC = \Delta CDA\] (g.c.g)
Suy ra AB = DC; AD = BC (hai cạnh tương ứng)
(A và B sai)
+ Xét \[\Delta ABO\] và \[\Delta CDO\] có:
\[\widehat {{A_2}} = \widehat {{C_2}}\] (cmt)
AB = DC (cmt)
\[\widehat {{B_1}} = \widehat {{D_1}}\] (cmt)
\[ \Rightarrow \Delta ABO = \Delta CDO\] (g.c.g)
Suy ra OA = OC; OB = OD (2 cạnh tương ứng)
(C đúng, D sai)
