7 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 CD Bài 10. Tính chất ba đường trung tuyến của tam giác (Thông hiểu) có đáp án

Trắc nghiệm Toán 7 Bài 10. Tính chất ba đường trung tuyến của tam giác có đáp án

Trắc nghiệm Toán 7 CD Bài 10. Tính chất ba đường trung tuyến của tam giác (Thông hiểu) có đáp án

230 lượt thi
7 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình vẽ sau.

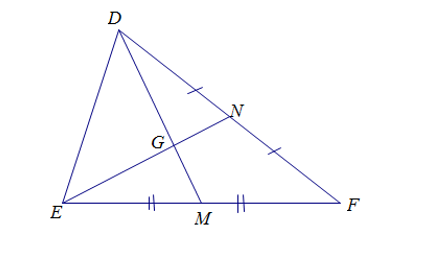
Tính $\frac{G N}{G E}$ .

A. 3;

B. $\frac{1}{3}$ ;

C. $\frac{1}{2}$ ;

D. 2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ba đường trung tuyến của một tam giác đồng quy tại một điểm.

Mà G là giao điểm của hai đường trung tuyến của tam giác DEF nên G là trọng tâm của tam giác DEF.

Do đó, $\frac{G E}{E N} = \frac{2}{3}$ ⇒ 3GE = 2EN ⇒3GE = 2(GE + GN) ⇒ GE = 2GN.

Vậy $\frac{G N}{G E} = \frac{1}{2}$ .

Câu 2:

Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là

A. 4,5 cm;

B. 3 cm;

C. 6 cm;

D. 4 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

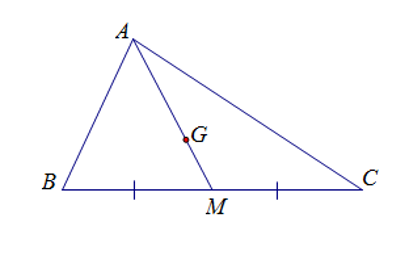
Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là (ảnh 1)

∆ABC có trung tuyến AM và trọng tâm G nên $A G = \frac{2}{3} . A M = \frac{2}{3} .9 = 6 (c m)$ .

Vậy AG = 6 cm.

Câu 3:

Cho ∆ABC có M là trung điểm của BC. G là trọng tâm của tam giác và AG = 12 cm. Tính độ dài đoạn thẳng AM.

A. 18 cm;

B. 16 cm;

C. 14 cm;

D. 13 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

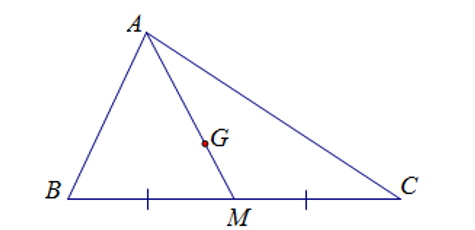
Cho tam giác ABC có M là trung điểm của BC. G là trọng tâm của tam giác và AG = 12 cm. (ảnh 1)

Tam giác ABC có M là trung điểm của AM nên AM là đường trung tuyến của ∆ABC.

G là trọng tâm của tam giác nên $\frac{A G}{A M} = \frac{2}{3} \Rightarrow A M = \frac{3}{2} A G = \frac{3}{2} .12 = 18 (c m)$ .

Vậy AM = 18 cm.

Câu 4:

Cho hình vẽ sau

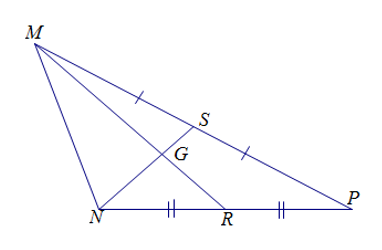
Biết MG = 3 cm. Tính MR.

A. 1 cm;

B. 2 cm;

C. 3 cm;

D. 4,5 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Vì G là giao điểm của hai đường trung tuyến của tam giác MNP nên G là trọng tâm của tam giác MNP.

$M G = \frac{2}{3} M R$ hay $3 = \frac{2}{3} M R \Rightarrow M R = \frac{9}{2} = 4, 5 (c m)$

Vậy MR = 4,5 cm.

Câu 5:

Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Kết luận đúng là

A. GM = GN;

B. $G M = \frac{1}{3} G B$ ;

C. $G N = \frac{1}{2} G C$ ;

D. GB = GC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

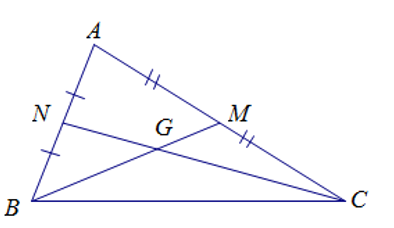
Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Kết luận đúng là (ảnh 1)

Vì G là giao điểm của hai đường trung tuyến của tam giác ABC nên G là trọng tâm của tam giác ABC.

$\frac{G M}{G B} = \frac{1}{2} \Rightarrow G M = \frac{1}{2} G B; \frac{G N}{G C} = \frac{1}{2} \Rightarrow G N = \frac{1}{2} G C$ .

Vậy kết luận đúng là $G N = \frac{1}{2} G C$ .

Câu 6:

Cho tam giác DEF cân tại D. Đường trung tuyến DI. Số đo góc DIE là

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

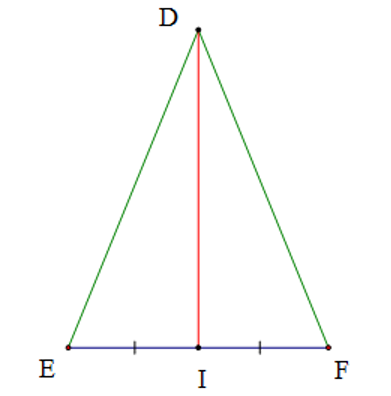
Cho tam giác DEF cân tại D. Đường trung tuyến DI. Số đo góc DIE là (ảnh 1)

Tam giác DEF cân tại D nên DE = DF (tính chất)

Xét ∆DEI và ∆DFI có

DE = DF

DI là cạnh chung

EI = FI (DI là trung tuyến)

Suy ra ∆DEI = ∆DFI (c.c.c)

Do đó $\hat{D I E} = \hat{D I F}$ (hai góc tương ứng)

Mà $\hat{D I E} + \hat{D I F} = 180 °$ (hai góc kề bù)

Nên $\hat{D I E} = \hat{D I F} = 90 °$ .

Câu 7:

Cho tam giác ABC cân tại A, hai đường trung tuyến BN và CP cắt nhau tại G. AG cắt BC tại M. Kết luận nào dưới đây sai?

A. BN = CP;

B. ∆GBC cân tại G;

C. AG ⊥ BC;

D. AM = BN.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

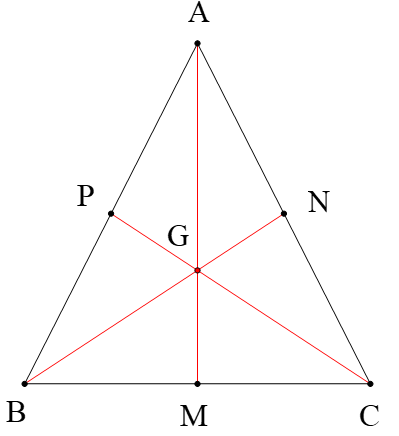
Cho tam giác ABC cân tại A, hai đường trung tuyến BN và CP cắt nhau tại G. (ảnh 1)

Tam giác ABC cân tại A nên AB = AC; $\hat{A B C} = \hat{A C B}$ (tính chất)

BN là trung tuyến nên AN = NC = $\frac{1}{2} A C$

CP là trung tuyến nên AP = BP = $\frac{1}{2} A B$

Do đó: AN = NC = AP = BP

Xét ∆BNC và ∆CPB có

NC = PB (chứng minh trên)

$\hat{N C B} = \hat{P B C}$

BC là cạnh chung

Suy ra ∆BNC = ∆CPB (c.g.c)

Do đó BN = CP (2 cạnh tương ứng)

BN và CP cắt nhau tại G nên G là trọng tâm tam giác ABC

Do đó $B G = \frac{2}{3} B N; C G = \frac{2}{3} C P$ (tính chất trọng tâm)

Mà BN = CP (chứng minh trên)

Suy ra BG = CG ⇒ Tam giác GBC cân tại G.

AG cắt BC tại M nên M là trung điểm của BC.

Xét ∆ABM và ∆ACM có

AB = AC

BM = CM (vì M là trung điểm của BC)

AM là cạnh chung

Suy ra ∆ABM và ∆ACM (c.c.c)

Do đó $\hat{A M B} = \hat{A M C}$ (hai góc tương ứng)

Mà $\hat{A M B} + \hat{A M C} = 180 °$ (hai góc kề bù)

Nên $\hat{A M B} = \hat{A M C} = 90 °$

Suy ra AM ⊥ BC hay AG ⊥ BC

Vậy AM = BN là kết luận sai.

Bắt đầu thi ngay

Trắc nghiệm Toán 7 Bài 10. Tính chất ba đường trung tuyến của tam giác có đáp án

Trắc nghiệm Toán 7 CD Bài 10. Tính chất ba đường trung tuyến của tam giác (Thông hiểu) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương