Trắc nghiệm Toán 7 Bài 1. Các góc ở vị trí đặc biệt có đáp án (Thông hiểu)
-
270 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho ba đường thẳng xy, zt, mn cắt nhau tại O sao cho ^zOm=58∘và ^yOt=35∘ (như hình vẽ).
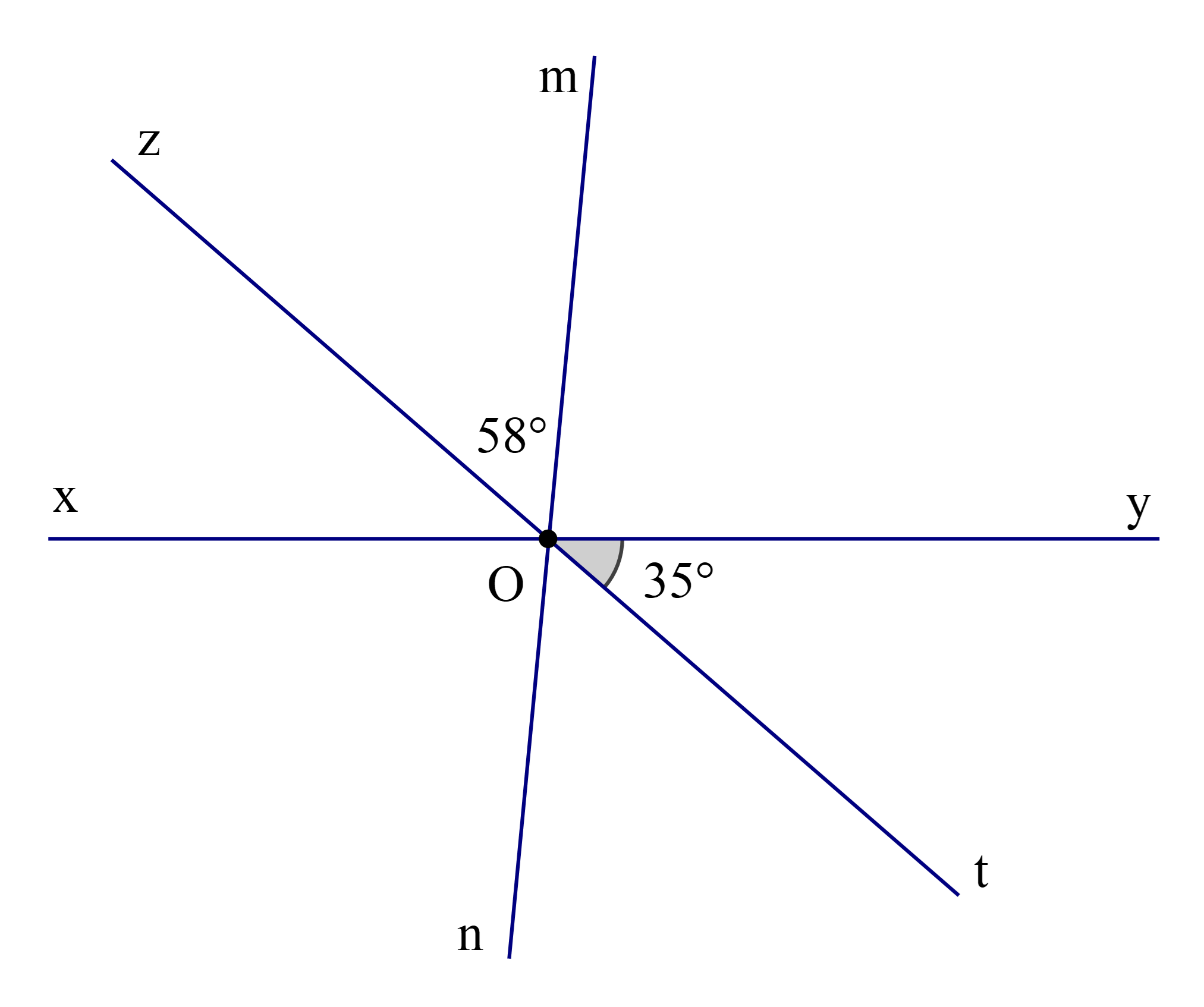
Số đo ^xOn là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có hai góc ^zOmvà ^tOnlà hai góc đối đỉnh nên:
^zOm=^tOn=58∘(tính chất hai góc đối đỉnh)
Ta lại có ^yOt+^tOn=^yOn (hai góc kề nhau)
Hay 35∘+58∘=^yOn
Suy ra ^yOn=93∘
Vì hai góc ^xOnv\`a^nOylà hai góc kề bù nên ta có:
^xOn+^nOy=180∘
Hay ^xOn+93∘=180∘
Suy ra ^xOn=180∘−93∘=87∘
Vậy ^xOn=87∘.
Câu 2:
Cho hình vẽ.
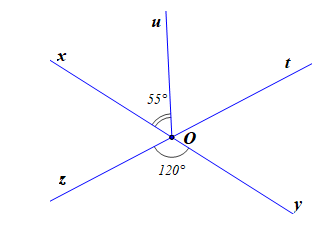
Số đo của ^uOt là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có ^xOt và ^zOy là hai góc đối đỉnh
Nên ^xOt=^zOy=120∘(tính chất hai góc đối đỉnh).
Ta lại có: ^xOu+^uOt=^xOt (hai góc kề nhau)
Hay 55∘+^uOt=120∘
Suy ra ^uOt=120∘−55∘=65∘
Vậy ^uOt=65∘.
Câu 3:
Hai đường thẳng AB và EF cắt nhau tại O. Kẻ tia ON nằm giữa hai tia OB và OE sao cho ^EON=^NOB. Gọi OM là tia đối của tia ON. Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
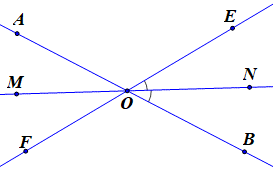
Theo bài ta có ^EON=^NOB (1)
Mà ^EON+^NOB=^EOB (2)
Thay (1) vào (2) ta có: ^NOB+^NOB=^EOB
Hay 2^NOB=^EOB
Suy ra ^NOB=12^EOB (3)
Ta lại có hai góc ^AOMv\`a^NOB là hai góc ở vị trí đối đỉnh nên:
^AOM=^NOB(tính chất hai góc đối đỉnh) (4)
Từ (3) và (4) suy ra ^AOM=12^EOB
Vậy ^AOM=12^EOB.
Câu 4:
Cho ba đường thẳng xy, zt, mn cắt nhau tại O sao ^nOy=120∘ và ^zOm=2^xOz. Số đo góc đối đỉnh của ^zOm bằng
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
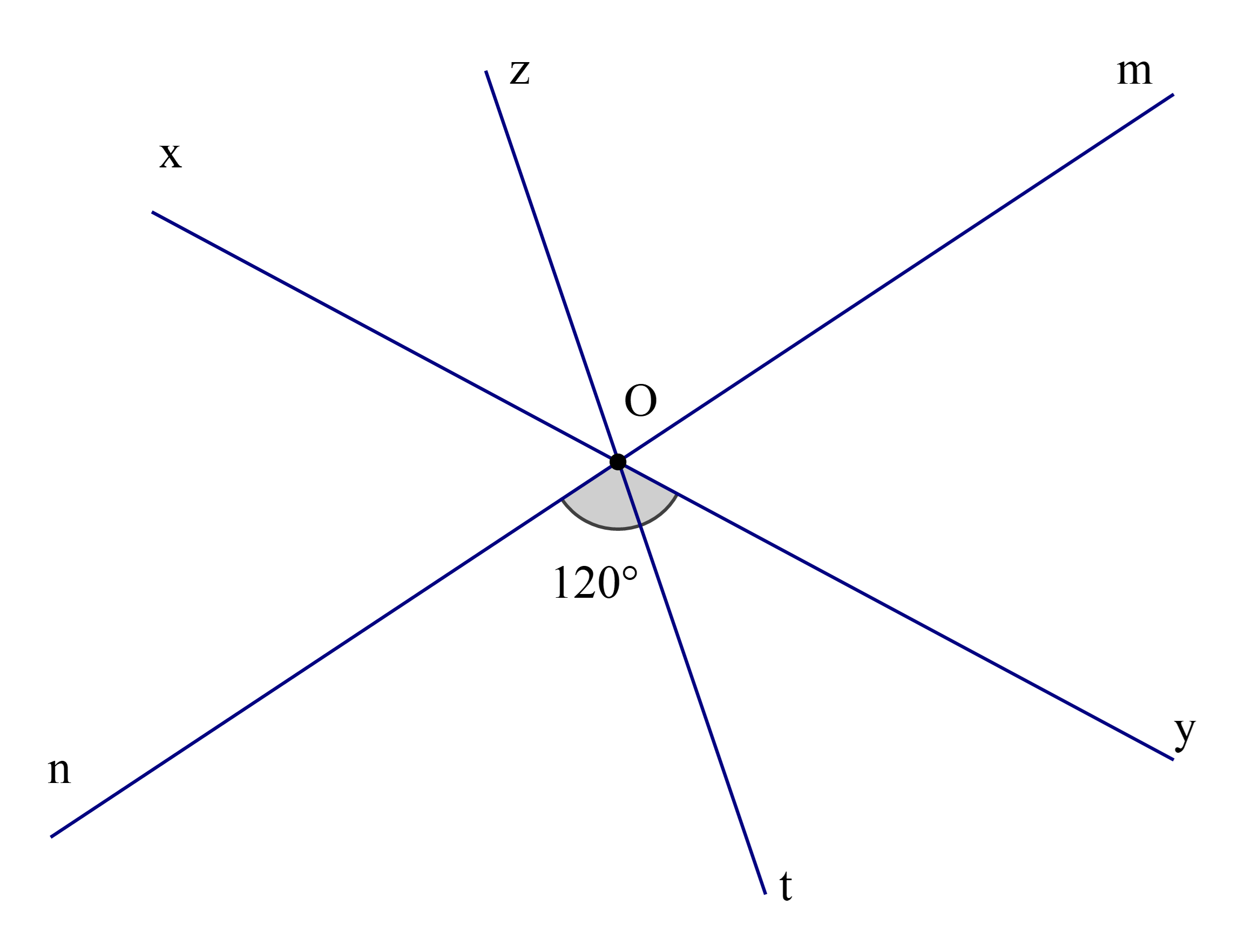
Vì hai đường thẳng xy và mn cắt nhau tại O nên hai góc ^xOmvà ^nOyở vị trí đối đỉnh.
Suy ra ^xOm=^nOy=120∘(tính chất hai góc đối đỉnh)
Ta có ^xOz+^zOm=^xOm (hai góc kề nhau)
Hay ^xOz+2^xOz=120∘(vì ^zOm=2^xOz)
Suy ra 3^xOz=120∘
Suy ra ^xOz=40∘
Từ đó ta có ^zOm=2^xOz=2.40∘=80∘
Do ^nOt và ^zOmlà hai góc đối đỉnh nên ^nOt=^zOm=80∘(tính chất hai góc đối đỉnh)
Vậy số đo góc đối đỉnh của ^zOm bằng 80°.
Câu 5:
Tìm giá trị của x trong hình sau:
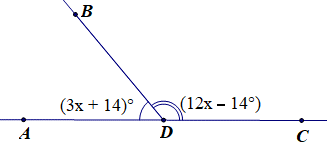
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có ^ADB+^BDC=180∘(hai góc kề bù)
Hay (3x + 14)° + (12x – 14)° = 180°
Suy ra (3x + 14 + 12x – 14)° = 180°
Do đó (15x)° = 180°
Suy ra 15x = 180
Nên x = 12
Vậy x = 12.
Ta chọn phương án B.
Câu 6:
Cho hình vẽ.
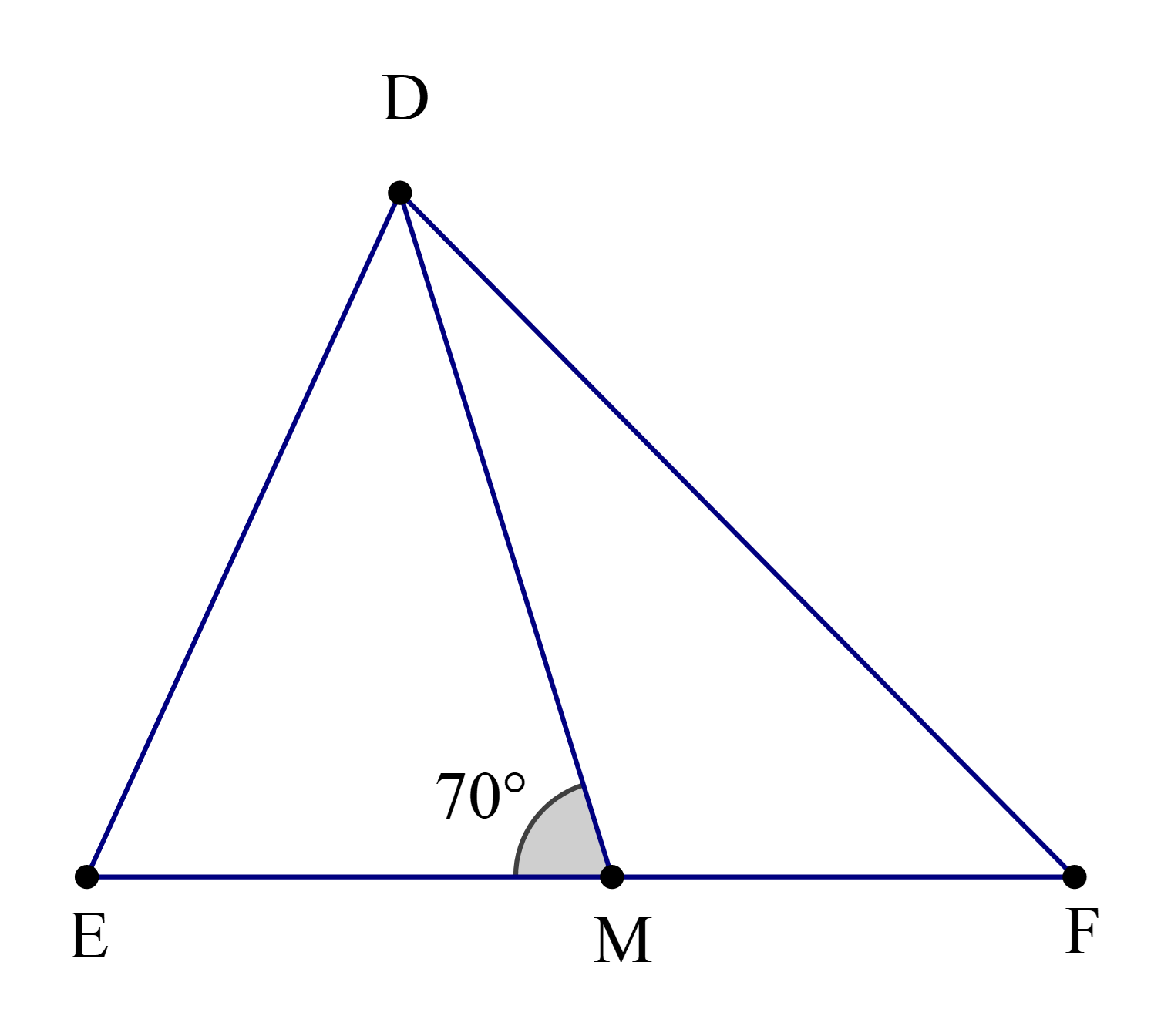
Số đo của ^DMFlà
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có hai góc ^DME và ^DMFở vị trí kề bù nên:
^DME+^DMF=180∘
Hay 70∘+^DMF=180∘
Suy ra ^DMF=180∘−70∘=110∘.
Vậy ^DMF=110∘.
Câu 7:
Cho hai góc ˆAvà ˆB là hai góc bù nhau, biết rằng ˆA=72∘.Chọn khẳng định đúng
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì hai góc ˆAvà ˆB là hai góc bù nhau nên:
ˆA+ˆB=180∘
Hay 72∘+ˆB=180∘
Suy ra ˆB=180∘−72∘=108∘
Suy ra 2ˆB=2.108∘=216∘ (1)
Ta lại có 3ˆA=3.72∘=216∘ (2)
Từ (1) và (2) suy ra 3ˆA=2ˆB.
Vậy 3ˆA=2ˆB.