11 câu hỏi trắc nghiệm thuộc Dạng 1: Nhận biết phân số với tử số và mẫu số là các số nguyên có đáp án

Trắc nghiệm Toán 6 Bài 23. Mở rộng phân số. Phân số bằng nhau có đáp án

Dạng 1: Nhận biết phân số với tử số và mẫu số là các số nguyên có đáp án

186 lượt thi
11 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Viết và đọc phân số trong trường hợp sau: Tử số là –4 và mẫu số là 3.

Xem đáp án

Ta viết được phân số là $\frac{- 4}{3}$ .

Đọc là: âm bốn phần ba.

Câu 2:

Phép chia 8 : (–19) được viết dưới dạng phân số là:

A. $\frac{- 19}{8}$

B. $\frac{8}{- 19}$

C. $\frac{18}{- 9}$

D. $\frac{- 9}{18}$

Xem đáp án

Đáp án đúng là: B

Phép chia 8 : (–19) được viết dưới dạng phân số là $\frac{8}{- 19}$ .

Câu 3:

Phép chia 79 : 3 được viết dưới dạng phân số là:

A. $\frac{3}{79}$

B. $\frac{97}{3}$

C. $\frac{79}{3}$

D. $\frac{- 3}{79}$

Xem đáp án

Đáp án đúng là: C

Phép chia 79 : 3 được viết dưới dạng phân số là $\frac{79}{3}$ .

Câu 4:

Số –5 được viết dưới dạng phân số là:

A. $\frac{- 5}{1}$

B. $\frac{1}{5}$

C. $\frac{- 1}{5}$

D. $\frac{- 5}{0}$

Xem đáp án

Đáp án đúng là: A

Số –5 được viết dưới dạng phân số là $\frac{- 5}{1}$ .

Câu 5:

Phân số $\frac{- 8}{10}$ đọc là:

A. Âm mười phần tám.

B. Mười phần tám.

C. Tám phần mười.

D. Âm tám phần mười.

Xem đáp án

Đáp án đúng là: D

Câu 6:

Cách viết nào sau đây cho ta một phân số?

A. $\frac{6}{0, 07}$

B. $\frac{- 3, 25}{81}$

C. $\frac{1}{0}$

D. $\frac{- 52}{14}$

Xem đáp án

Đáp án đúng là: D

Đáp án A: Mẫu số là số thập phân nên $\frac{6}{0, 07}$ không là phân số.

Đáp án B: Tử số là số thập phân nên $\frac{- 3, 25}{81}$ không là phân số.

Đáp án C: Mẫu bằng 0 nên $\frac{1}{0}$ không là phân số.

Đáp án D: Tử số và mẫu số là các số nguyên và mẫu số khác 0 nên $\frac{- 52}{14}$ là phân số.

Câu 7:

Phần tô màu biểu diễn phân số nào?

A. $\frac{10}{3}$

B. $\frac{3}{7}$

C. $\frac{3}{10}$

D. $\frac{3}{9}$

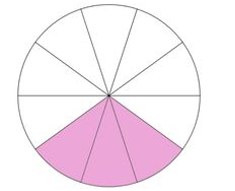
Xem đáp án

Đáp án đúng là: C

Quan sát hình tròn ta thấy hình tròn được chia làm 10 phần. Phần tô màu chiếm 3 phần.

Vậy phân số biểu thị phần tô màu là $\frac{3}{10}$ .

Câu 8:

Cho phân số $A = \frac{30}{n - 7}$ (n ∈ ℤ), tìm tất cả các giá trị của n để A là phân số.

A. n ≠ 7.

B. n = 7.

C. n = 30.

D. n ≠ 30.

Xem đáp án

Đáp án đúng là: A

Để $A = \frac{30}{n - 7}$ là phân số thì n – 7 ≠ 0.

Vậy n ≠ 7.

Câu 9:

Cho tập H = {6; 2; 7}. Có thể viết được tất cả bao nhiêu phân số có tử và mẫu thuộc tập H và tử khác mẫu?

A. 7.

B. 6.

C. 8.

D. 5.

Xem đáp án

Đáp án đúng là: B

Với tử và mẫu số đều thuộc tập H và tử khác mẫu, ta có thể viết được các phân số:

$\frac{6}{2}; \frac{6}{7}; \frac{2}{6}; \frac{2}{7}; \frac{7}{6}; \frac{7}{2}$ .

Vậy có thể viết được 6 phân số.

Câu 10:

Cho phân số $B = \frac{- 1}{n^{2} + 9}$ (n ∈ ℤ). Khẳng định nào sao đây là sai

A. Không có giá trị nào của n để B là phân số.

B. n = 0 thì B là phân số.

C. n = –5 thì B là phân số .

D. n = 100 thì B là phân số.

Xem đáp án

Đáp án đúng là: A

Ta có n² ≥ 0 với mọi n ∈ ℤ.

Nên n² + 9 ≥ 9 với mọi n ∈ ℤ.

Suy ra n² + 9 ≠ 0 với mọi n ∈ ℤ.

Vậy $B = \frac{- 1}{n^{2} + 9}$ luôn là phân số với mọi n ∈ ℤ.

Nên đáp án A là sai.

Câu 11:

Tìm các số tự nhiên n để phân số $\frac{n + 2}{n}$ có giá trị là số nguyên.

A. {–1; –2; 1; 2}.

B. {–1; 1}.

C. {1; 2}.

D. {–2; 2}.

Xem đáp án

Đáp án đúng là: C

Ta có $\frac{n + 2}{n} = \frac{n}{n} + \frac{2}{n} = 1 + \frac{2}{n}$ .

Để $\frac{n + 2}{n}$ có giá trị là số nguyên thì $\frac{2}{n}$ là số nguyên.

Vậy n ∈ Ư(2) = {–2; –1; 1; 2}.

Mà n là số tự nhiên nên n ∈ {1; 2}.

Bắt đầu thi ngay

Trắc nghiệm Toán 6 Bài 23. Mở rộng phân số. Phân số bằng nhau có đáp án

Dạng 1: Nhận biết phân số với tử số và mẫu số là các số nguyên có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương