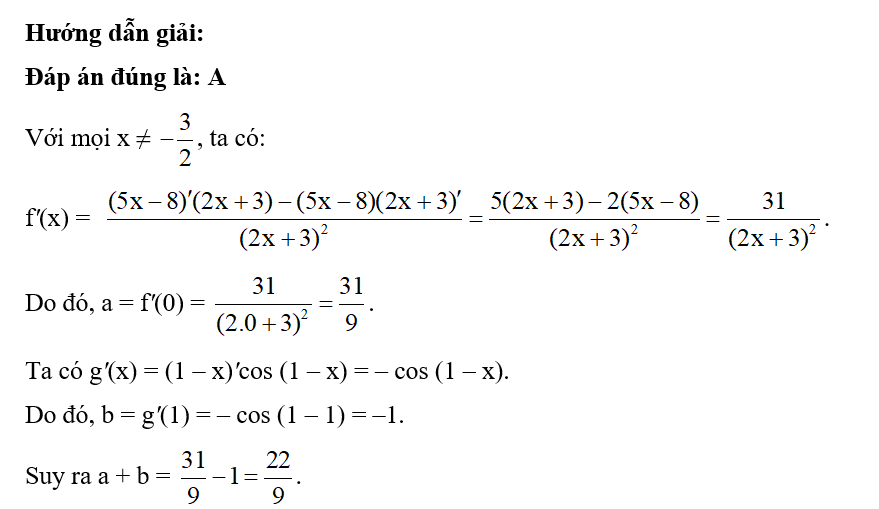10 câu hỏi trắc nghiệm thuộc Dạng 2. Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương các hàm số và đạo hàm của hàm số hợp

Trắc nghiệm Toán 11 Bài 32. Các quy tắc tính đạo hàm có đáp án

Dạng 2. Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương các hàm số và đạo hàm của hàm số hợp

190 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Đạo hàm của hàm số y = sin(2x – 1) là:

A. 2cos(2x – 1);

B. cos(2x – 1);

C. – 2cos(2x – 1);

D. – cos(2x – 1).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Ta có y'(x) = (2x – 1)'cos(2x – 1) = 2cos(2x – 1).

Câu 2:

Đạo hàm của hàm số y = (2x + 7)(3x – 5) tại điểm x₀ = 4 là:

A. –31;

B. 5;

C. 59;

D. 11.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có y'(x) = (2x + 7)'(3x – 5) + (2x + 7)(3x – 5)' = 2(3x – 5) + 3(2x + 7) = 12x + 11.

y'(4) = 12 . 4 + 11 = 59.

Câu 3:

Đạo hàm của hàm số y = (– x – 6)⁵ tại điểm x₀ = –3 là:

A. 81;

B. –81;

C. 405;

D. –405.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có y'(x) = 5 . (–x – 6)⁴ . (–x – 6)' = –5(–x – 6)⁴.

y'(–3) = –5(3 – 6)⁴ = –405.

Câu 4:

Đạo hàm của hàm số y = e^{12x + 4} là:

A. e^{12x + 4};

B. 12e^{12x + 4};

C. –12e^{12x + 4;}

D. –e^{12x + 4}.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có y'(x) = (12x + 4)'. e^{12x + 4} = 12e^{12x + 4}.

Câu 5:

Đạo hàm của hàm số y = log₄(9x – 2) tại điểm x₀ = $\frac{1}{3}$ là:

A. $\frac{1}{\ln 4}$ ;

B. $\frac{9}{\ln 4}$ ;

C. $\frac{9}{(9 x - 2) \ln 4}$ ;

\frac{2}{\ln 4}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Với x > $\frac{2}{9}$ , ta có: y'(x) = $\frac{(9 x - 2)^{'}}{(9 x - 2) \ln 4} = \frac{9}{(9 x - 2) \ln 4}$ .

Vì $\frac{1}{3} > \frac{2}{9}$ nên $(\frac{1}{3}) = \frac{9}{(9 \cdot \frac{1}{3} - 2) \ln 4} = \frac{9}{\ln 4}$ .

Câu 6:

Đạo hàm của hàm số y = cot(3x² – x + 2) là:

A. $- \frac{6 x - 1}{\sin^{2} (3 x^{2} - x + 2)}$ ;

B. $\frac{6 x - 1}{\sin^{2} (3 x^{2} - x + 2)}$ ;

C. $\frac{1 - 6 x}{\sin^{2} (3 x^{2} - x + 2)}$ ;

- \frac{6 x - 1}{\sin (3 x^{2} - x + 2)}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Ta có y'(x) = $- \frac{(3 x^{2} - x + 2)^{'}}{\sin^{2} (3 x^{2} - x + 2)} = - \frac{6 x - 1}{\sin^{2} (3 x^{2} - x + 2)}$ .

Câu 7:

Đạo hàm của hàm số $y = \frac{1}{4 x^{5} + 3 x^{3} - 8 x^{2} + 10}$ tại điểm x₀ = 1 là:

A. $\frac{13}{81}$ ;

B. $- \frac{13}{9}$ ;

C. $- \frac{13}{81}$ ;

\frac{13}{9}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có $= - \frac{(4 x^{5} + 3 x^{3} - 8 x^{2} + 10)^{'}}{{(4 x^{5} + 3 x^{3} - 8 x^{2} + 10)}^{2}} = - \frac{20 x^{4} + 9 x^{2} - 16 x}{{(4 x^{5} + 3 x^{3} - 8 x^{2} + 10)}^{2}}$ .

$(1) = - \frac{{20.1}^{4} + {9.1}^{2} - 16.1}{{({4.1}^{5} + {3.1}^{3} - {8.1}^{2} + 10)}^{2}} = - \frac{13}{9^{2}} = - \frac{13}{81}$ .

Câu 8:

Đạo hàm của hàm số y = 4^{7x – 6} tại điểm x₀ = 1 là:

A. 4ln4;

B. 28ln7;

C. 28ln4;

D. 4ln7.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có y'(x) = (7x – 6)'. 4^{7x – 6} . ln4 = 7 . 4^{7x – 6} . ln4.

y'(1) = 7 . 4^{7.1 – 6} . ln4 = 28ln4.

Câu 9:

Cho đạo hàm của hàm số f(x) = $\frac{5 x - 8}{2 x + 3}$ tại điểm x₀ = 0 bằng a. Đạo hàm của hàm số g(x) = sin(1 – x) tại điểm x₀ = 1 bằng b. Khi đó a + b có giá trị bằng

A. $\frac{22}{9}$ ;

B. $\frac{4}{3}$ ;

C. $\frac{7}{3}$ ;

D. 0.

Xem đáp án

Cho đạo hàm của hàm số f(x) = 5x-8 / 2x+ 3 tại điểm x0 = 0 bằng a. Đạo hàm của hàm số (ảnh 1)

Câu 10:

Cho đạo hàm của hàm số f(x) = x³ + 6x – 9 tại điểm x₀ = –3 bằng a. Đạo hàm của hàm số g(x) = (1 – x)(2x + 1) tại điểm x₀ = –5 bằng b. Kết luận nào sau đây là đúng?

A. a = b;

B. b > a;

C. a > b;

D. a ≤ b.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có f'(x) = (x³)' + (6x)' – (9)' = 3x² + 6.

Khi đó, a = f(–3) = 3 . (–3)² + 6 = 33.

Lại có g'(x) = (1 – x)'(2x + 1) + (1 – x)(2x + 1)' = – (2x + 1) + 2(1 – x) = – 4x + 1.

Khi đó, b = g'(–5) = – 4 . (–5) + 1 = 21.

Suy ra a > b (do 33 > 21).

Bắt đầu thi ngay

Trắc nghiệm Toán 11 Bài 32. Các quy tắc tính đạo hàm có đáp án

Dạng 2. Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương các hàm số và đạo hàm của hàm số hợp

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương