15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 CTST Bài tập cuối chương 7 (Thông hiểu) có đáp án

Câu 1:

Cho tam thức bậc hai f(x) = x² – 10x + 2. Kết luận nào sau đây đúng?

A. f(–2) < 0;

B. f(1) > 0;

C. f(–2) > 0;

D. f(1) = 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có:

⦁ f(1) = 1² – 10.1 + 2 = –7 < 0.

Do đó phương án B, D sai.

⦁ f(–2) = (–2)² – 10.(–2) + 2 = 26 > 0.

Do đó phương án C đúng, phương án A sai.

Vậy ta chọn phương án C.

Câu 2:

Cho tam thức bậc hai f(x) = –2x² + 8x – 8. Trong các mệnh đề sau, mệnh đề nào đúng?

A. f(x) < 0, ∀x ∈ ℝ;

B. f(x) ≥ 0, ∀x ∈ ℝ;

C. f(x) ≤ 0, ∀x ∈ ℝ;

D. f(x) > 0, ∀x ∈ ℝ.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Tam thức bậc hai f(x) = –2x² + 8x – 8 có ∆ = 8² – 4.(–2).(–8) = 0.

Suy ra f(x) có nghiệm kép $x = - \frac{8}{2. (- 2)} = 2$ .

Ta có a = –2 < 0.

Do đó f(x) < 0 với mọi x ≠ 2

Hay f(x) ≤ 0 với mọi x ∈ ℝ.

Do đó ta chọn phương án C.

Câu 3:

Bảng xét dấu nào sau đây là của f(x) = 6x² + 37x + 6?

A.

Bảng xét dấu nào sau đây là của f(x) = 6x^2 + 37x + 6 (ảnh 2)

B.

Bảng xét dấu nào sau đây là của f(x) = 6x^2 + 37x + 6 (ảnh 3)

C.

Bảng xét dấu nào sau đây là của f(x) = 6x^2 + 37x + 6 (ảnh 4)

D.

Bảng xét dấu nào sau đây là của f(x) = 6x^2 + 37x + 6 (ảnh 5)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Tam thức bậc hai f(x) = 6x² + 37x + 6 có ∆ = 37² – 4.6.6 = 1225 > 0.

Do đó f(x) có hai nghiệm phân biệt là:

$x_{1} = \frac{- 37 + \sqrt{1225}}{2.6} = - \frac{1}{6}; x_{2} = \frac{- 37 - \sqrt{1225}}{2.6} = - 6$

Ta có a = 6 > 0.

Ta có bảng xét dấu f(x) như sau:

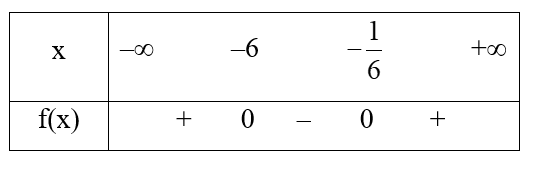
Bảng xét dấu nào sau đây là của f(x) = 6x^2 + 37x + 6 (ảnh 1)

Vậy ta chọn phương án B.

Câu 4:

Cho tam thức bậc hai f(x) = x² + 1. Mệnh đề nào sau đây đúng nhất?

A. f(x) > 0 ⇔ x ∈ (–∞; +∞);

B. f(x) = 0 ⇔ x = –1;

C. f(x) < 0 ⇔ x ∈ (–∞; 1);

D. f(x) > 0 ⇔ x ∈ (0; 1).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Tam thức bậc hai f(x) = x² + 1 có ∆ = 0² – 4.1.1 = –4 < 0.

Suy ra f(x) vô nghiệm.

Ta có a = 1 > 0.

Vậy f(x) > 0, ∀x ∈ ℝ hay f(x) > 0 ⇔ x ∈ (–∞; +∞).

Ta chọn phương án A.

Câu 5:

Cho hàm số y = f(x) = ax² + bx + c có đồ thị như hình vẽ.

Cho hàm số y = f(x) = ax^2 + bx + c có đồ thị như hình vẽ. Đặt delta = b^2 – 4ac. (ảnh 1)

Đặt ∆ = b² – 4ac. Chọn khẳng định đúng?

A. a > 0, ∆ > 0;

B. a < 0, ∆ > 0;

C. a > 0, ∆ = 0;

D. a < 0, ∆ = 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Quan sát đồ thị, ta thấy:

⦁ Đồ thị y = f(x) cắt trục Ox tại hai điểm phân biệt có hoành độ lần lượt là x₁ = 1; x₂ = 4.

Suy ra f(x) có 2 nghiệm phân biệt x₁ = 1; x₂ = 4.

Do đó ∆ > 0.

⦁ Trên khoảng (–∞; 1) và (4; +∞), ta có f(x) > 0. Suy ra a > 0.

Vậy ta có a > 0, ∆ > 0.

Ta chọn phương án A.

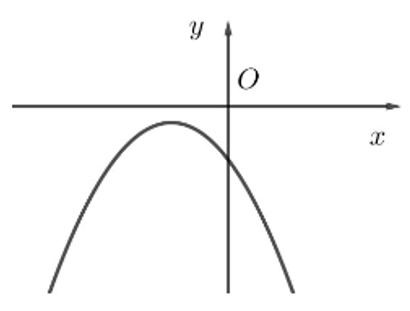
Câu 6:

Cho hàm số y = f(x) có đồ thị như hình bên.

Bảng xét dấu của tam thức bậc hai tương ứng là:

A.

Cho hàm số y = f(x) có đồ thị như hình bên. Bảng xét dấu của tam thức bậc hai tương ứng (ảnh 3)

B.

Cho hàm số y = f(x) có đồ thị như hình bên. Bảng xét dấu của tam thức bậc hai tương ứng (ảnh 4)

C.

Cho hàm số y = f(x) có đồ thị như hình bên. Bảng xét dấu của tam thức bậc hai tương ứng (ảnh 5)

D.

Cho hàm số y = f(x) có đồ thị như hình bên. Bảng xét dấu của tam thức bậc hai tương ứng (ảnh 6)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Quan sát đồ thị, ta thấy f(x) < 0, với mọi x ∈ ℝ.

Do đó ta có bảng xét dấu của f(x) như sau:

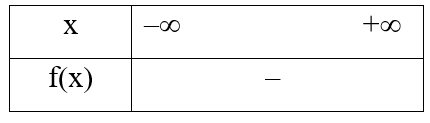
Cho hàm số y = f(x) có đồ thị như hình bên. Bảng xét dấu của tam thức bậc hai tương ứng (ảnh 2)

Vậy ta chọn phương án C.

Câu 7:

Cho f(x) = –x² – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?

A. 5;

B. 7;

C. 10;

D. Vô số.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Tam thức bậc hai f(x) = –x² – 4x + 5 có ∆’ = (–2)² – (–1).5 = 9 > 0.

Suy ra f(x) có hai nghiệm phân biệt là:

$x_{1} = \frac{- (- 2) + \sqrt{9}}{- 1} = - 5; x_{2} = \frac{- (- 2) - \sqrt{9}}{- 1} = 1.$

Ta lại có a = –1 < 0.

Do đó ta có:

⦁ f(x) âm trên hai khoảng (–∞; –5) và (1; +∞);

⦁ f(x) dương trên khoảng (–5; 1);

⦁ f(x) = 0 khi x = –5 hoặc x = 1.

Vì vậy bất phương trình f(x) ≥ 0 có tập nghiệm là [–5; 1].

Trên đoạn [–5; 1], ta thấy có 7 giá trị nguyên là: –5; –4; –3; –2; –1; 0; 1.

Vậy ta chọn phương án B.

Câu 8:

Tập nghiệm của bất phương trình x² – 3x + 2 < 0 là:

A. (1; 2);

B. (–∞; 1) ∪ (2; +∞);

C. (–∞; 1);

D. (2; +∞).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Tam thức bậc hai f(x) = x² – 3x + 2 có ∆ = (–3)² – 4.1.2 = 1 > 0.

Do đó f(x) có hai nghiệm phân biệt là:

$x_{1} = \frac{- (- 3) - \sqrt{1}}{2.1} = 1; x_{2} = \frac{- (- 3) + \sqrt{1}}{2.1} = 2.$

Ta lại có a = 1 > 0.

Do đó ta có:

⦁ f(x) âm trên khoảng (1; 2);

⦁ f(x) dương trên hai khoảng (–∞; 1) và (2; +∞);

⦁ f(x) = 0 khi x = 1 hoặc x = 2.

Vì vậy bất phương trình x² – 3x + 2 < 0 có tập nghiệm là (1; 2).

Ta chọn phương án A.

Câu 9:

Tập nghiệm của bất phương trình x² + 9 > 6x là:

A. (3; +∞);

B. ℝ \ {3};

C. ℝ;

D. (–∞; 3).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có x² + 9 > 6x.

⇔ x² – 6x + 9 > 0.

Tam thức bậc hai f(x) = x² – 6x + 9 có ∆’ = (–3)² – 1.9 = 0.

Suy ra f(x) có nghiệm kép x = 3.

Ta lại có a = 1 > 0.

Do đó ta có:

⦁ f(x) dương trên hai khoảng (–∞; 3) và (3; +∞);

⦁ f(x) = 0 khi x = 3.

Vì vậy bất phương trình x² – 6x + 9 > 0 có tập nghiệm là (–∞; 3) ∪ (3; +∞) (hoặc ta có thể viết: ℝ \ {3}).

Ta chọn phương án B.

Câu 10:

Tập xác định của hàm số $y = \frac{2 x + 3}{\sqrt{- 2 x^{2} + 8 x - 12}}$ là:

A. ℝ;

B. (2; 6);

C. ∅;

D. (–∞; 2) ∪ (6; +∞).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Hàm số xác định khi và chỉ khi –2x² + 8x – 12 > 0.

Tam thức bậc hai f(x) = –2x² + 8x – 12 có ∆’ = 4² – (–2).(–12) = –8 < 0.

Do đó f(x) vô nghiệm.

Ta lại có a = –2 < 0.

Vì vậy f(x) < 0, với mọi x ∈ ℝ.

Vậy bất phương trình –2x² + 8x – 12 > 0 có tập nghiệm là ∅.

Ta chọn phương án C.

Câu 11:

Cho hàm số bậc hai f(x) có đồ thị như hình bên.

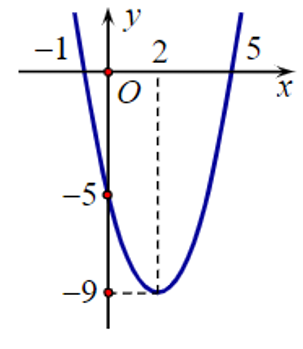
Tập nghiệm của bất phương trình f(x) ≥ 0 là:

A. (–1; 5);

B. (–∞; –1) ∪ (5; +∞);

C. (–∞; –1] ∪ [5; +∞);

D. [–1; 5].

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Quan sát đồ thị, ta thấy f(x) ≥ 0 khi và chỉ khi x ≤ –1 hoặc x ≥ 5.

Vì vậy tập nghiệm của bất phương trình f(x) ≥ 0 là (–∞; –1] ∪ [5; +∞).

Ta chọn phương án C.

Câu 12:

Phương trình

\sqrt{4 x^{2} - 3} = x

có nghiệm là:

A. x = 1;

B. x = –1;

C. x = 1 hoặc x = –1;

D. Vô nghiệm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Bình phương hai vế của phương trình trên, ta được:

4x² – 3 = x²

⇒ 3x² – 3 = 0

⇒ x = 1 hoặc x = –1.

Với x = 1, ta có $\sqrt{{4.1}^{2} - 3} = 1$ (đúng)

Với x = –1, ta có $\sqrt{4. {(- 1)}^{2} - 3} = - 1$ (vô lí)

Vì vậy khi thay các giá trị x = 1 và x = –1 vào phương trình đã cho, ta thấy chỉ có x = 1 thỏa mãn.

Vậy phương trình đã cho có nghiệm là x = 1.

Ta chọn phương án A.

Câu 13:

Cho phương trình $\sqrt{x^{2} + 3} = \sqrt{2 x + 6}$ . Khẳng định nào sau đây sai?

A. Tổng các nghiệm của phương trình đã cho là 2;

B. Tích các nghiệm của phương trình đã cho là –5;

C. Các nghiệm của phương trình đã cho đều lớn hơn –2;

D. Phương trình có hai nghiệm trái dấu.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Bình phương hai vế của phương trình đã cho, ta được:

x² + 3 = 2x + 6

⇒ x² – 2x – 3 = 0

⇒ x = 3 hoặc x = –1.

Với x = 3, ta có $\sqrt{3^{2} + 3} = \sqrt{2.3 + 6}$ (đúng)

Với x = –1, ta có $\sqrt{{(- 1)}^{2} + 3} = \sqrt{2. (- 1) + 6}$ (đúng)

Vì vậy khi thay các giá trị x = 3 và x = –1 vào phương trình đã cho, ta thấy cả x = 3 và x = –1 đều thỏa mãn.

Vậy phương trình đã cho có hai nghiệm là x = 3 và x = –1.

• Tổng các nghiệm là: 3 + (–1) = 2. Do đó phương án A đúng.

• Tích các nghiệm là: 3.(–1) = –3. Do đó phương án B sai.

• Ta có x = 3 > –2 và x = –1 > –2.

Vì vậy các nghiệm của phương trình đã cho đều lớn hơn –2. Do đó phương án C đúng.

• Ta có x = 3 > 0 và x = –1 < 0.

Vì vậy phương trình đã cho có hai nghiệm trái dấu. Do đó phương án D đúng.

Vậy ta chọn phương án B.

Câu 14:

Giá trị x nào sau đây là nghiệm của phương trình $\sqrt{2 x^{2} + 3 x - 5} = x + 1$ ?

A. x = –3;

B. x = 2;

C. Cả A và B đều đúng;

D. Cả A và B đều sai.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Bình phương hai vế của phương trình đã cho, ta được:

2x² + 3x – 5 = (x + 1)²

⇒ 2x² + 3x – 5 = x² + 2x + 1

⇒ x² + x – 6 = 0

⇒ x = 2 hoặc x = –3.

Với x = 2, ta có $\sqrt{{2.2}^{2} + 3.2 - 5} = 2 + 1$ (đúng)

Với x = –3, ta có $\sqrt{2 {(- 3)}^{2} + 3. (- 3) - 5} = - 3 + 1$ (sai)

Vì vậy khi thay lần lượt các giá trị x = 2 và x = –3 vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 2.

Ta chọn phương án B.

Câu 15:

Số nghiệm của phương trình $\sqrt{- x^{2} + 4 x} = 2 x - 2$ là:

A. 0;

B. 1;

C. 2;

D. 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Bình phương hai vế của phương trình đã cho, ta được:

–x² + 4x = (2x – 2)²

⇒ –x² + 4x = 4x² – 8x + 4

⇒ 5x² – 12x + 4 = 0

⇒ x = 2 hoặc $x = \frac{2}{5}$

Với x = 2, ta có $\sqrt{- 2^{2} + 4.2} = 2.2 - 2$ (đúng)

Với $x = \frac{2}{5}$ , ta có $\sqrt{- {(\frac{2}{5})}^{2} + 4. \frac{2}{5}} = 2. \frac{2}{5} - 2$ (sai)

Vì vậy khi thay lần lượt các giá trị x = 2 và $x = \frac{2}{5}$ vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.

Vậy phương trình đã cho có một nghiệm duy nhất.

Ta chọn phương án B.

Trắc nghiệm Toán 10 CTST Bài tập cuối chương 7 (Phần 2) có đáp án

Trắc nghiệm Toán 10 CTST Bài tập cuối chương 7 (Thông hiểu) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương