8 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (Thông hiểu)

Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2)

Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (Thông hiểu)

305 lượt thi
8 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tam giác ABC có $\hat{B}$ = 60°, $\hat{C}$ = 45° và AB = 7. Tính độ dài cạnh AC.

A. AC =

$\frac{5 \sqrt{6}}{2}$ ;

B. AC =

$\frac{7 \sqrt{6}}{2}$ ;

C. AC =

$7 \sqrt{2}$ ;

D. AC = 10.

Xem đáp án

Đáp án đúng là: B

Theo định lý sin trong tam giác ABC, ta có:

Câu 2:

Cho tam giác ABC có M là trung điểm của BC, I là trung điểm AM. Khẳng định nào sau đây là đúng?

A. $\vec{A I} = \frac{1}{4} (\vec{A B} + \vec{A C})$ ;

$\vec{A I} = \frac{1}{4} (\vec{A B} - \vec{A C})$ ;

$\vec{A I} = \frac{1}{4} \vec{A B} + \frac{1}{2} \vec{A C}$ ;

$\vec{A I} = \frac{1}{4} \vec{A B} - \frac{1}{2} \vec{A C}$ .

Xem đáp án

Đáp án đúng là: A

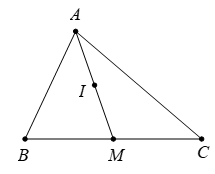
Cho tam giác ABC có M là trung điểm của BC, I là trung điểm AM. Khẳng định nào sau đây là đúng? (ảnh 1)

Vì M là trung điểm BC nên $\vec{A B} + \vec{A C} = 2 \vec{A M} .$ (1)

Mặt khác I là trung điểm AM nên $2 \vec{A I} = \vec{A M} .$ (2)

Từ (1), (2) suy ra $\vec{A B} + \vec{A C} = 4 \vec{A I} \Leftrightarrow \vec{A I} = \frac{1}{4} (\vec{A B} + \vec{A C}) .$

Câu 3:

Giá trị của biểu thức S = 2 + sin²90° + 2cos² 60° − 3tan² 45° bằng:

$\frac{1}{2}$ ;

$\frac{- 1}{2}$ ;

C. 1;

D. 3.

Xem đáp án

Đáp án đúng là: A

Áp dụng bảng giá trị lượng giác của các góc đặc biệt, ta có:

S = 2 + sin²90° + 2cos² 60° − 3tan² 45° = 2 + 1² + 2. ${(\frac{1}{2})}^{2}$ − 3.1² = $\frac{1}{2}$ .

Câu 4:

Tam giác ABC có AB = 4, BC = 6, AC = $2 \sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.

A. AM = $4 \sqrt{2}$ ;

B. AM = 3;

C. AM =

$2 \sqrt{3}$ ;

D. AM =

$3 \sqrt{2}$ .

Xem đáp án

Đáp án đúng là: C

Tam giác ABC có AB = 4, BC = 6, AC = 2 căn 7 . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM. (ảnh 1)

Câu 5:

Cho vectơ $\vec{M N}$ và điểm P bất kì nằm trên mặt phẳng. Tìm tập hợp điểm Q sao cho $|\vec{M N}| = |\vec{P Q}|$ ?

A. Q thuộc vectơ

$\vec{M N}$ ;

B. Tập hợp điểm Q nằm trên đường tròn tâm P có bán kính bằng độ dài vectơ

$\vec{M N}$ ;

C. Tập hợp điểm Q nằm trên đường tròn tâm M có bán kính bằng độ dài vectơ

$\vec{N P}$ ;

D. Tập hợp điểm Q nằm trên đường tròn tâm N có bán kính bằng độ dài vectơ

$\vec{N P}$ .

Xem đáp án

Đáp án đúng là: B

Ta có: $|\vec{M N}| = |\vec{P Q}|$ ⇒ MN = PQ. Suy ra tập hợp điểm Q thỏa mãn yêu cầu đề bài là đường tròn tâm P có bán kính bằng độ dài vectơ $\vec{M N}$ .

Câu 6:

Cho tam giác ABC đều cạnh a. Tính độ dài vectơ $\vec{A B}$ + $\vec{A C}$ .

$a \sqrt{3}$ ;

B. 2

$a \sqrt{3}$ ;

$\frac{a \sqrt{3}}{2}$ ;

$\frac{a \sqrt{2}}{2}$ .

Xem đáp án

Đáp án đúng là: A

Cho tam giác ABC đều cạnh a. Tính độ dài vectơ AB + AC (ảnh 1)

Câu 7:

Cho hình thoi ABCD. Giá trị của $(\vec{A B} + \vec{A D}) . (\vec{B A} + \vec{B C})$ bằng

A. 1;

B. 0;

C. AB² – BC²;

D. AB² + BC².

Xem đáp án

Đáp án đúng là: B

Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau, do đó $\vec{A C} ⊥ \vec{B D}$ $\Rightarrow$ $\vec{A C} . \vec{B D} = 0$ .

Mà ABCD là hình thoi nên nó cũng là hình bình hành, do đó áp dụng quy tắc hình bình hành ta có: $(\vec{A B} + \vec{A D}) . (\vec{B A} + \vec{B C})$ = $\vec{A C} . \vec{B D}$ = 0.

Câu 8:

Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Giá trị của $\vec{B A} . \vec{B C}$ bằng

A. 0;

B. c²;

C. a² – b²;

D. a².

Xem đáp án

Đáp án đúng là: B

Tam giác ABC vuông tại A

Suy ra AB ^ AC $\Rightarrow$ $\vec{A B} . \vec{A C} = 0$ $\Rightarrow \vec{B A} . \vec{A C} = 0$ .

Ta có: $\vec{B A} . \vec{B C} = \vec{B A} . (\vec{B A} + \vec{A C}) = {\vec{B A}}^{2} + \vec{B A} . \vec{A C} = A B^{2} = c^{2}$ .

Bắt đầu thi ngay

Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2)

Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương