Trắc nghiệm Toán 10 Bài 4. Tổng và hiệu hai vectơ có đáp án
Trắc nghiệm Toán 10 Bài 4. Tổng và hiệu hai vectơ có đáp án
-
247 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho ba điểm A, B, C phân biệt. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét các đáp án:
- Đáp án A sai vì →BA+⇀AC=⇀BC. Mà A ; B ; C bất kỳ nên →AB+→AC=→BC là khẳng định sai.
- Đáp án B. Ta có : →MP+→NM=→NM+→MP=→NP. Vậy B đúng.
- Đáp án C sai vì →AB+⇀AD=⇀AC
nếu ABCD là hình bình hành thì →AB+⇀AD=⇀AC
- Đáp án D. Ta có : →AA+→BB=→0+→0=→0≠→AB. Vậy D sai
Câu 2:
Cho →a và →b là các vectơ khác →0 với →a là vectơ đối của →b. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có : →a=−→b. Do đó, →a và →b cùng phương, cùng độ dài và ngược hướng nhau.
Câu 3:
Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét các đáp án:
- Đáp án A. Ta có →CA−→BA=→CA+→AB=→CB=−→BC. Vậy A sai.
- Đáp án B sai vì nếu ABDC là hình bình hành thì →AB+⇀AD=⇀AC phải là ABDC là hình bình hành mới đúng.
- Đáp án C. Ta có →AB+→CA=→CA+→AB=→CB. Vậy C đúng.
Câu 4:
Cho →AB=−→CD. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Ta có: →AB=−→CD=→DC. Do đó:
+) →AB và →CD ngược hướng.
+) →AB và →CD cùng độ dài.
+) ABCD là hình bình hành nếu →AB và →CD không cùng giá. Khẳng định này không có cơ sở.
+) →AB+→CD=→0. Khẳng định này không có cơ sở.
Câu 5:
Tính tổng →MN+→PQ+→RN+→NP+→QR.
 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Ta có : →MN+→PQ+→RN+→NP+→QR=→MN+→NP+→PQ+→QR+→RN=→MN.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Điều kiện để I là trung điểm AB là →IA=−→IB;
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là : B
Điều kiện cần và đủ để I là trung điểm của đoạn thẳng AB là →IA=−→IB⇔→IA+→IB=→0.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án đúng là : A
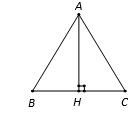
Tam giác ABC cân ở A, đường cao AH. Do đó, H là trung điểm BC (tính chất tam giác cân).
Ta có:
- AB=AC⇒|→AB|=|→AC|. Do đó, B đúng.
- H là trung điểm BC⇒{→HC=−→HB→BC=2→HC. Do đó, C, D đúng.
Câu 9:
Cho tam giác ABC đều cạnh a. Tính |→AB+→AC|.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
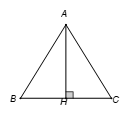
Gọi H là trung điểm của BC⇒AH⊥BC.
Xét tam giác vuông AHC ta có:
AH2+HC2=AC2
⇔AH=√AC2−HC2
⇔AH=√a2−a24
Suy ra AH=BC√32=a√32.
Ta lại có |→AB+→AC|=|→AH+→HB+→AH+→HC|=|2→AH|
Suy ra : |2→AH|=2.a√32=a√3
Câu 10:
Cho tam giác ABC vuông cân tại A có AB = a. Tính |→AB+→AC|
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
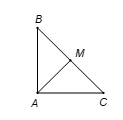
Gọi M là trung điểm BC⇒AM=12BC. (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông).
Ta có : |→AB+→AC|=|→AM+→MB+→AM+→MC|
⇔|→AB+→AC|=|2→AM|=2AM=BC=a√2.
Câu 11:
Cho tam giác ABC vuông cân tại C và AB=√2. Tính độ dài của →AB+→AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
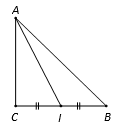
Ta có : AC2+BC2=AB2 Suy ra, 2.AC2=AB2
⇔AC2=AB22=1 ⇒AC=CB=1.
Gọi I là trung điểm BC⇒AI=√AC2+CI2=√12+(12)2=√52
Khi đó
→AC+→AB=→AI+→IC+→AI+→IB=2→AI⇒|→AC+→AB|=2|→AI|=2.√52=√5.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
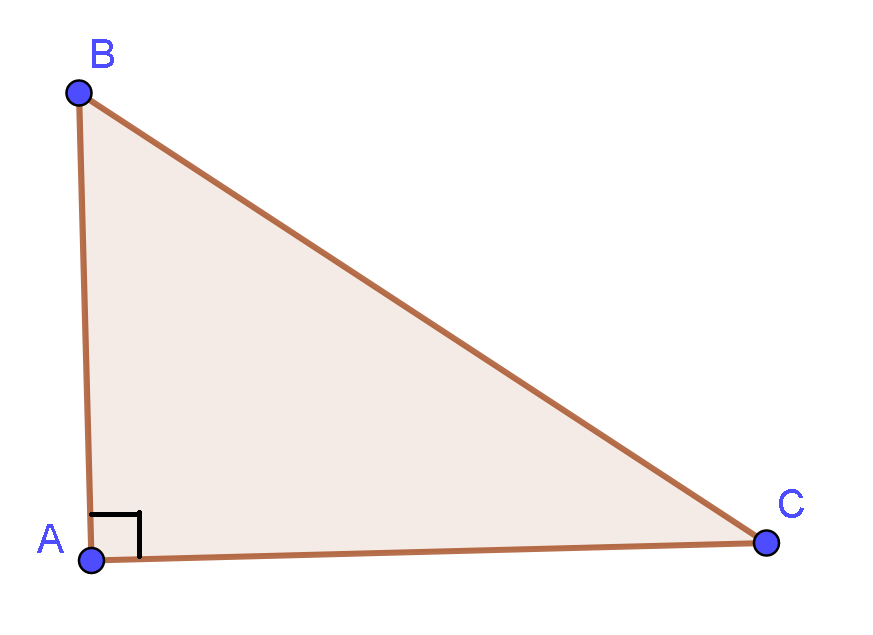
Ta có: |→CA+→AB|=|→CB|=CB
Áp dụng định lí Py – ta – go cho tam giác vuông ABC ta có:
CB=√AC2+AB2=√32+42=5 hay |→CA+→AB|=|→CB|=CB= 5
Câu 13:
Cho 5 điểm bất kỳ A, B, C, D, E. Tính tổng →CD+→EC+→DA+→BE
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
→CD+→EC+→DA+→BE = (→CD+→DA)+(→BE+→EC)
⇔→CA+→BC= →BC+→CA= →BA
Câu 14:
Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu →CB - →AB
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
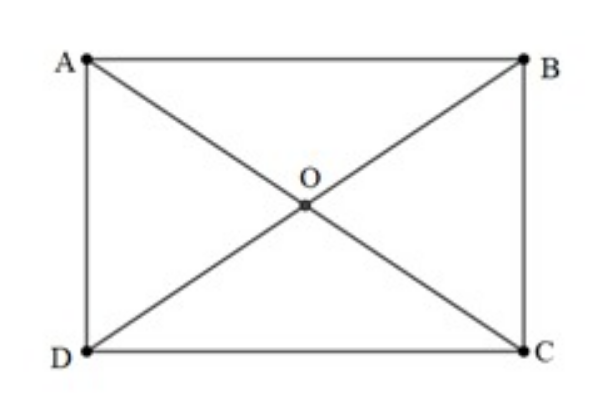
Ta có: |→BA|=|→AB|=AB và →BA ngược hướng với →AB⇔→BA=−→AB
→CB−→AB=→CB+(−→AB)=→CB+→BA=→CA
Câu 15:
Cho hình chữ nhật ABCD, hai đường đường chéo AC và BD cắt nhau tại O. Tính hiệu →AD - →AB
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
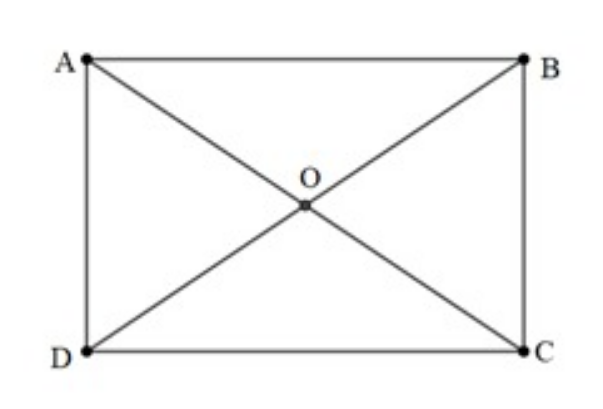
Áp dụng quy tắc 3 điểm cho A, B, D ta có: →AD - →AB = →BD.
