Trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳng (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳng (Phần 2) có đáp án (Vận dụng)
-
335 lượt thi
-
5 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
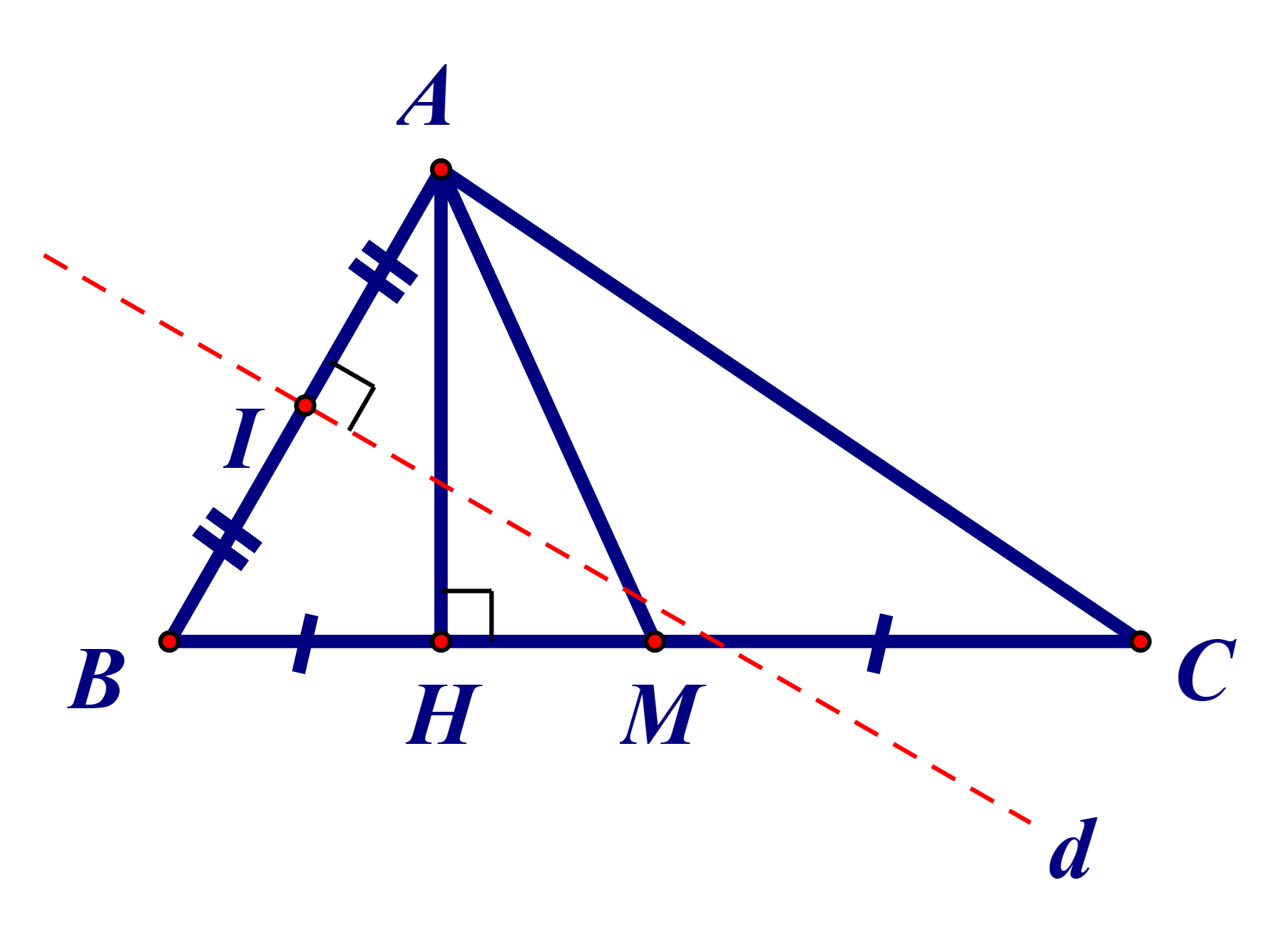
Ta có A ∈ AM.
Suy ra tọa độ A(1 + 3t; –2 – 7t).
Lại có A ∈ AH.
Suy ra 2(1 + 3t) + 5(–2 – 7t) + 66 = 0.
Do đó –29t + 58 = 0.
Vì vậy –29t = –58.
Khi đó t = 2.
Suy ra tọa độ A(7; –16).
Gọi I là trung điểm của cạnh AB.
Suy ra \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{7 + 4}}{2} = \frac{{11}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{ - 16 - 3}}{2} = - \frac{{19}}{2}\end{array} \right.\)
Khi đó tọa độ \(I\left( {\frac{{11}}{2}; - \frac{{19}}{2}} \right)\).
Ta có \(\overrightarrow {AB} = \left( { - 3;13} \right)\).
Đường trung trực d của cạnh AB đi qua điểm \(I\left( {\frac{{11}}{2}; - \frac{{19}}{2}} \right)\) và có vectơ pháp tuyến \(\overrightarrow {AB} = \left( { - 3;13} \right)\).
Suy ra phương trình d: \( - 3\left( {x - \frac{{11}}{2}} \right) + 13\left( {y + \frac{{19}}{2}} \right) = 0\).
⇔ 3x – 13y – 140 = 0.
Vậy ta chọn phương án B.
Câu 2:
Cho điểm M nằm trên ∆: x + y – 1 = 0 và cách N(–1; 3) một khoảng bằng 5. Khi đó tọa độ điểm M là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Chọn A(0; 1) ∈ ∆.
Đường thẳng ∆ có vectơ pháp tuyến \(\vec n = \left( {1;1} \right)\).
Suy ra đường thẳng ∆ nhận \(\vec u = \left( {1; - 1} \right)\) làm vectơ chỉ phương.
Đường thẳng ∆ đi qua A(0; 1) và có vectơ chỉ phương \(\vec u = \left( {1; - 1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = t\\y = 1 - t\end{array} \right.\)
Ta có M ∈ ∆. Suy ra M(t; 1 – t).
Ta có \(\overrightarrow {NM} = \left( {t + 1; - 2 - t} \right)\).
Suy ra \(NM = \left| {\overrightarrow {NM} } \right| = \sqrt {{{\left( {t + 1} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \).
Theo đề, ta có MN = 5.
⇔ (t + 1)2 + (–2 – t)2 = 25.
⇔ t2 + 2t + 1 + 4 + 4t + t2 = 25.
⇔ 2t2 + 6t – 20 = 0.
⇔ t = 2 hoặc t = –5.
Với t = 2, ta có tọa độ M(2; –1).
Với t = –5, ta có tọa độ M(–5; 6).
Vậy ta chọn phương án A.
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
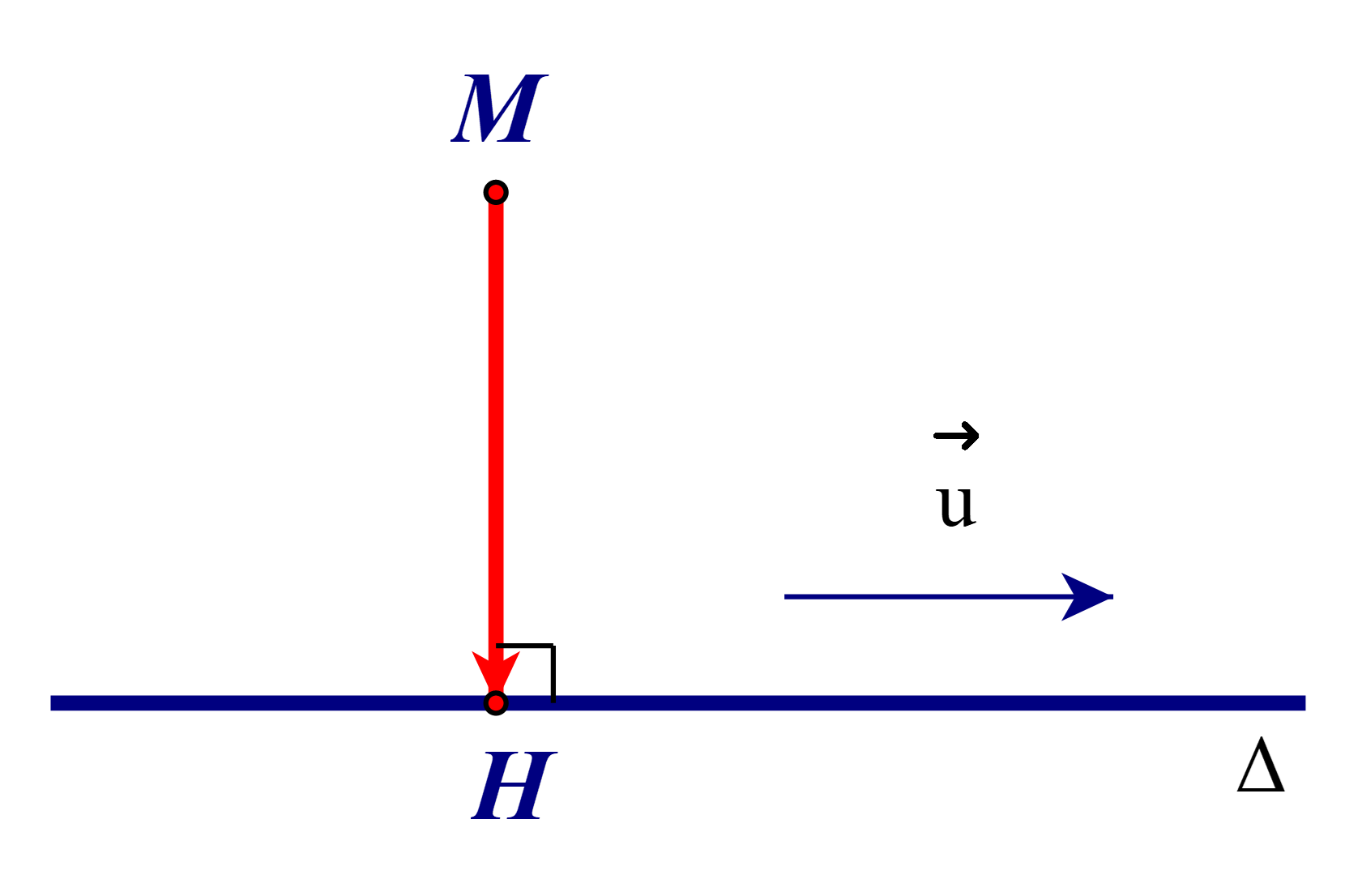
Thế tọa độ điểm M(4; 5) vào phương trình ∆, ta được: \(\left\{ \begin{array}{l}4 = 2 - 3t\\5 = 1 + 2t\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}t = - \frac{2}{3}\\t = 2\end{array} \right.\)
Suy ra M(4; 5) ∉ ∆.
Gọi H là hình chiếu của M lên ∆.
Ta có H ∈ ∆. Suy ra tọa độ H(2 – 3t; 1 + 2t).
Ta có \(\overrightarrow {MH} = \left( { - 2 - 3t; - 4 + 2t} \right)\).
Đường thẳng ∆ có vectơ chỉ phương \(\vec u = \left( { - 3;2} \right)\).
Ta có \(\overrightarrow {MH} \bot \vec u\).
Suy ra \(\overrightarrow {MH} .\vec u = 0\).
Khi đó (–2 – 3t).(–3) + (–4 + 2t).2 = 0.
Vì vậy 13t – 2 = 0.
Suy ra \(t = \frac{2}{{13}}\).
Do đó tọa độ \(H\left( {\frac{{20}}{{13}};\frac{{17}}{{13}}} \right)\).
Vậy hoành độ hình chiếu H của điểm M lên đường thẳng ∆ là: \(\frac{{20}}{{13}} \approx 1,538\).
Vậy ta chọn phương án D.
Câu 4:
Cho hai điểm A(–2; 1), B(3; 5) và đường thẳng d: \(\left\{ \begin{array}{l}x = - 5 + 2t\\y = 9 - 5t\end{array} \right.\). Tọa độ của điểm H ∈ d thỏa mãn \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right|\) đạt giá trị nhỏ nhất là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có H ∈ d. Suy ra H(–5 + 2t; 9 – 5t).
Ta có:
⦁ \(\overrightarrow {HA} = \left( { - 2t + 3;5t - 8} \right)\);
⦁ \(\overrightarrow {HB} = \left( { - 2t + 8;5t - 4} \right)\). Suy ra \(2\overrightarrow {HB} = \left( { - 4t + 16;10t - 8} \right)\).
Suy ra \(\overrightarrow {HA} - 2\overrightarrow {HB} = \left( {2t - 13; - 5t} \right)\).
Ta có \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right| = \sqrt {{{\left( {2t - 13} \right)}^2} + {{\left( { - 5t} \right)}^2}} = \sqrt {29{t^2} - 52t + 169} \)
\( = \sqrt {29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right]} \)
Ta có \({\left( {t - \frac{{26}}{{29}}} \right)^2} \ge 0,\,\,\forall t \in \mathbb{R}\)
\( \Leftrightarrow {\left( {t - \frac{{26}}{{29}}} \right)^2} + \frac{{4225}}{{841}} \ge \frac{{4225}}{{841}},\,\,\forall t \in \mathbb{R}\)
\( \Leftrightarrow 29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right] \ge 29.\frac{{4225}}{{841}} = \frac{{4225}}{{29}},\,\,\forall t \in \mathbb{R}\)
\[ \Leftrightarrow \sqrt {29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right]} \ge \sqrt {\frac{{4225}}{{29}}} = \frac{{65\sqrt {29} }}{{29}},\,\,\forall t \in \mathbb{R}\].
Dấu “=” xảy ra \( \Leftrightarrow t = \frac{{26}}{{29}}\).
Với \(t = \frac{{26}}{{29}}\), ta có \(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Khi đó \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right|\) đạt giá trị nhỏ nhất bằng \[\frac{{65\sqrt {29} }}{{29}}\] khi \(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Vậy ta chọn phương án A.
Câu 5:
Đường thẳng d trong hình bên biểu thị tổng lít nước được bơm vào một bể nước theo thời gian (đơn vị: giờ).
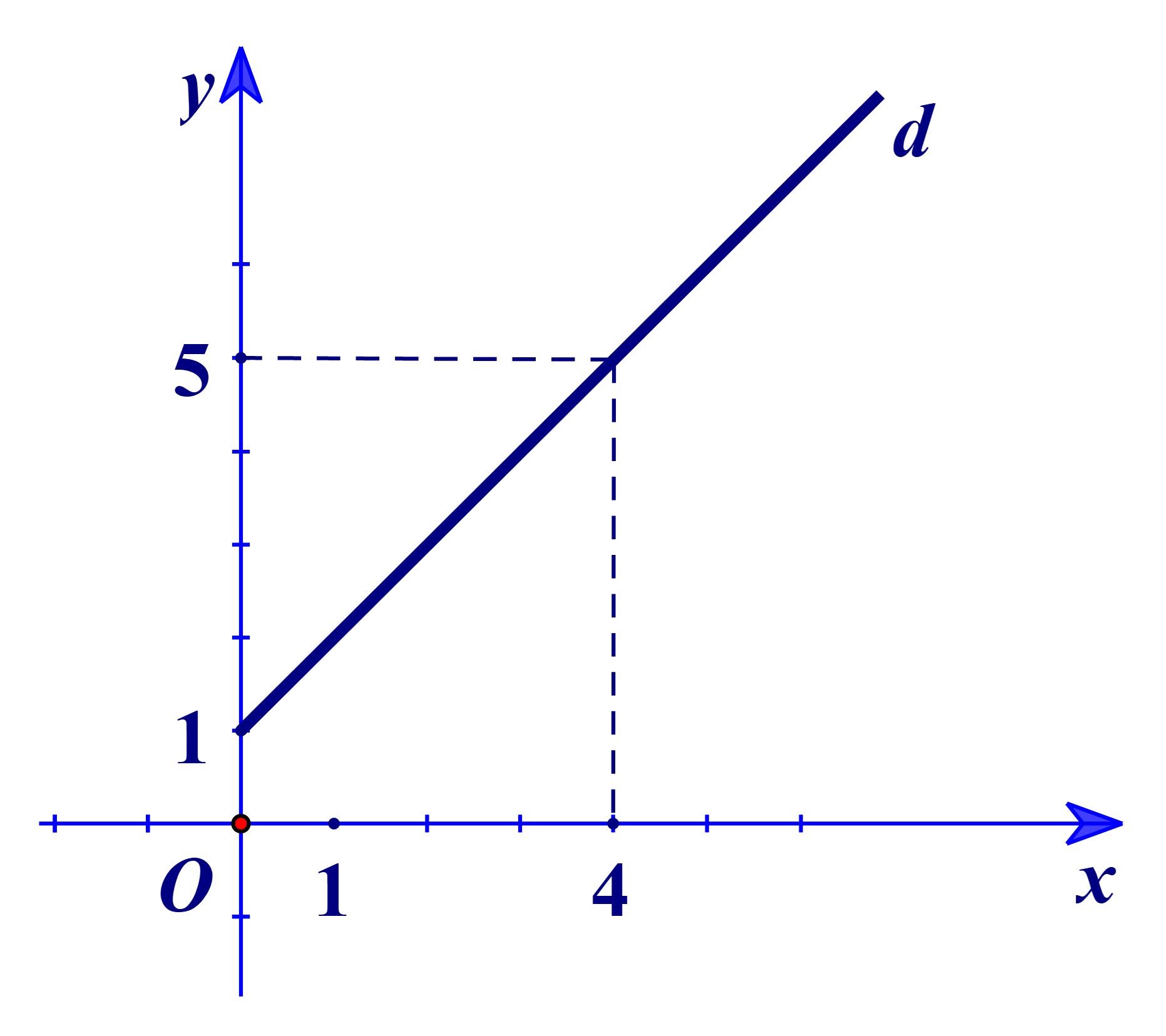
Tổng lít nước mà bể đó chứa sau 15 giờ bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Quan sát hình vẽ, ta thấy đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (4; 5).
Suy ra phương trình d: \(\frac{{x - 0}}{{4 - 0}} = \frac{{y - 1}}{{5 - 1}}\)
\( \Leftrightarrow \frac{x}{4} = \frac{{y - 1}}{4}\)
⇔ x = y – 1
⇔ y = x – 1.
Ta có: 15 giờ ứng với x = 15.
Với x = 15, ta có y = 15 – 1 = 14 (lít nước).
Vậy sau 15 giờ, bể nước chứa 14 lít nước.
Do đó ta chọn phương án A.
