Trắc nghiệm Toán 10 Bài 2. Biểu thức toạ độ của các phép toán vectơ có đáp án
Trắc nghiệm Toán 10 Bài 2. Biểu thức toạ độ của các phép toán vectơ có đáp án
-
1289 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho →a = (2; – 4), →b= (– 5; 3). Tìm tọa độ của →a + →b.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có : →a + →b = (2 + (– 5); – 4 + 3) = (– 3; – 1).
Câu 2:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : A
Ta có : →m−→n = (3 – (– 1)); – 4 – 2) = (4; – 6).
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có: 2→m= 2(–1; 2) = (–2; 4)
2→m+→n = (– 2 + 5); 4 – 7) = (3; – 3).
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : A
Tọa độ điểm I là nghiệm của hệ phương trình: {xI=−1+12=0yI=1+12=1⇒I(0;1).
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: 3→k= 3(5 ; 2) = (15 ; 6) ; 2→n = 2(10 ; 8) = (20 ; 16)
3→k−2→n = (15 – 20 ; 6 – 16) = (– 5; – 10).
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có {→AB=(−2;−1)→AC=(−3;−2) ⇒→AB−→AC = (– 2 – (– 3); – 1 – (– 2)) = (1; 1).
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi điểm B có tọa độ (xB ; yB)
Vì I là trung điểm của AB nên ta có :
{xI=2+xB2=4yI=−3+yB2=7⇔{xI=2.4−2=6yI=2.7−(−3)=17 ⇒ B(6; 17).
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : D
Gọi toạ độ trọng tâm G (xG; yG), ta có :
{xG=3+1+53=3yG=5+2+23=3 ⇒G (3; 3).
Câu 9:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi toạ độ C(x ; y), ta có:
Vì G là trọng tâm tam giác ABC nên : {xG=6+(−3)+x3=−1yG=1+5+y3=1
⇒{x=−6y=−3. hay C (–6; –3).
Câu 10:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
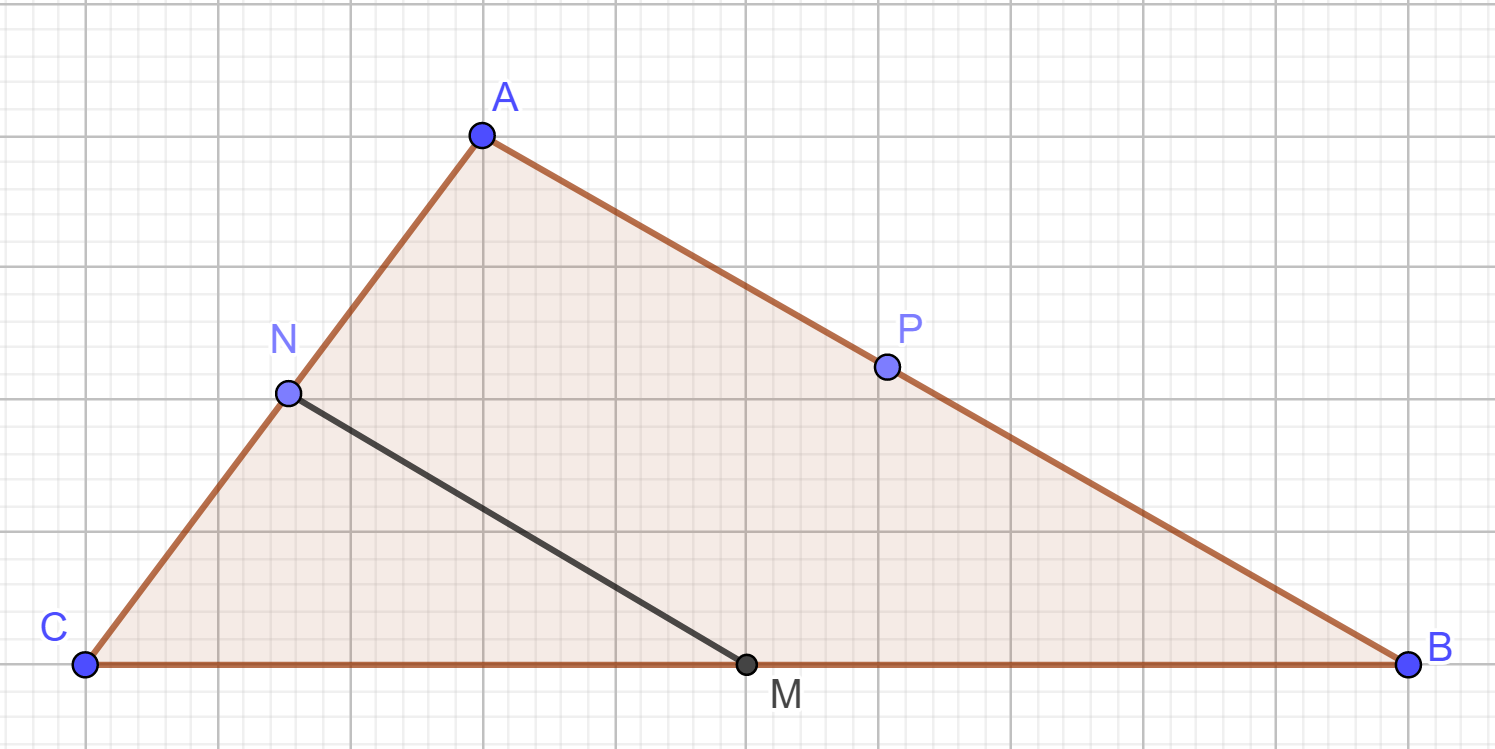
Gọi toạ độ A (x ; y).
Ta có : →PA = (x + 1; y – 6) và →MN = (–2; –7)
Theo tính chất đường trung bình tam giác, ta có:
→MN= 12→AB = →PA
Khi đó (1)⇔{x+1=−2y−6=−7 ⇔{x=−3y=−1
Hay A (–3; –1).
Câu 11:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Xét tam giác ABC, có :
M là trung điểm AB
N là trung điểm AC
Suy ra MN là đường trung bình tam giác ABC
Theo tính chất đường trung bình, ta có :
→MN=12→BC = 12.(2; –8) = (1; –4).
Câu 12:
Trong hệ tọa độ Oxy cho tam giác ABC có C (–2 ; –4), trọng tâm G (0 ; 4) và trung điểm cạnh BC là M (2 ; 0). Tổng hoành độ của điểm A và B là.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Vì M là trung điểm BC nên ta có : {xB=2xM−xCyB=2yM−yC
⇔{xB=2.2−(−2)=6yB=2.0−(−4)=4⇒B (6; 4).
Vì G là trọng tâm tam giác ABC nên {xA=3xG−xB−xCyA=3yG−yB−yC
⇔{xA=3.0−6−(−2)yA=3.4−4−(−4)⇔{xA=−4yA=12 hay A (–4 ; 12).
Suy ra xA+xB= 6 + (–4) = 2.
Câu 13:
Trong hệ tọa độ Oxy cho tam giác ABC có A (– 2 + x ; 2), B (3 ; 5 + 2y), C(x ; 3 – y). Tìm tổng 2x + y với x, y để O (0 ; 0) là trọng tâm tam giác ABC?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Vì O là trọng tâm tam giác ABC nên, ta có : {xG=−2+x+3+x3=0yG=2+5+2y+3−y3=0
⇒{x=−12y=−10⇒2.x+y=2.(−12)+(−10)=−11.
Câu 14:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi toạ độ điểm C (x ; y).
Vì G là trọng tâm tam giác ABC nên ta có : {xG=6+(−3)+x3=−1yG=1+5+y3=1
⇒{x=−6y=−3 hay C (–6; –3).
Câu 15:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có : →a−→b = (–2m; 2) – (2; –7n) = (–2m –2; 2 + 7n)
Mà →a−→b = (6; – 5)
Nên ta có: {−2m−2=62+7n=−5⇔{m=−4n=−1
Vậy m = – 4 và n = – 1.
