19 câu hỏi trắc nghiệm thuộc Trắc nghiệm Đại số và Giải tích 11 Bài 1-2: Phương pháp quy nạp toán học

Câu 1:

Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?

Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:

A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”

Chứng minh :

Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”

Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.

Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1

Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k

Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.

Vậy A(n) đúng với mọi n ∈N*

A. Bước 1

B. Bước 2

C. Bước 3

D. Không có bước nào sai

Xem đáp án

Đáp án là C. Ta có a,b∈N* không suy ra a -1, b -1∈N* . Do vậy không áp dụng được giả thiết quy nạp cho cặp {a -1, b -1}.

Chú ý: nêu bài toán trên đúng thì ta suy ra mọi số tự nhiên đều bằng nhau. Điều này là vô lí.

Câu 2:

Mạnh cầm một tờ giấy và lấy kéo cắt thành 7 mảnh sau đó nhặt một trong số bảy mảnh giấy đã cắt và lại cắt thành 7 mảnh. Mạnh cứ tiếp tục cắt như vậy. Sau một hồi, Mạnh thu lại và đếm tất cả các mảnh giấy đã cắt. Hỏi kết quả nào sau đây có thể xảy ra?

A. Mạnh thu được 122 mảnh

B. Mạnh thu được 123 mảnh

C. Mạnh thu được 120 mảnh

D. Mạnh thu được 121 mảnh

Xem đáp án

Mỗi lần cắt một mảnh giấy thành 7 mảnh, tức là Mạnh tạo thêm 6 mảnh giấy. Do đó công thức tính số mảnh giấy theo n bước được thực hiện là Sn = 6n + 1. Ta chứng minh tính đúng đắn của công thức trên bằng phương pháp quy nạp theo n.

Bước cơ sở. Mạnh cắt mảnh giấy thành 7 mảnh, n =1, S(1) = 6.1+1 =7

Công thức đúng với n = 1

Bước quy nạp: giả sử sau k bước, Mạnh nhận được số mảnh giấy là S(k) = 6k + 1

Sang bước thứ k +1, Mạnh lấy một trong số những mảnh giấy nhận được trong k bước trước và cắt thành 7 mảnh. Tức là Mạnh đã lấy đi 1 trong S(k) mảnh và thay vào đó 7 mảnh được cắt ra. Vậy tổng số mảnh giấy ở bước k + 1 là: S(k =1) = S(k) -1 + 7= S(k) + 6 = 6k + 1 + 6 = 6(k+1) +1

Vậy công thức S(n) đúng với mọi n ∈N* . Theo công thức trên chỉ có phương án D thoả mãn vì 121 =6.20 + 1

Đáp án D

Câu 3:

Cho dãy số (un) xác định bởi $u_{n} = n^{2} - 4 n - 2$ . Khi đó $u_{10}$ bằng:

A. 48

B. 60

C. 58

D. 10

Xem đáp án

u10 = 102 – 4.20 – 2 =58

Đáp án C

Câu 4:

Cho dãy số $u_{n} = 1 + (n + 3) . 3^{n}$ . khi đó công thức truy hồi của dãy là:

A. $u_{n + 1} = 1 + 3 u_{n} v ớ i n ⩾ 1$

B. $u_{n + 1} = 1 + 3 u_{n} + 3^{n + 1} v ớ i n \geq 1$

C. $u_{n + 1} = u_{n} + 3^{n + 1} v ớ i n \geq 1$

D. $u_{n + 1} = 3 u_{n} + 3^{n + 1} - 2 v ớ i n \geq 1$

Xem đáp án

un+1 = 1+ (n+4).3n+1 = 1 + (n+3).3n+1 + 3n+1

= 1 + 3n.(n+3).3 + 3n+1 = 3[1 + (n+ 3).3n] + 3n+1 – 2 = 3un + 3n+1 -2

Đáp án là D

Câu 5:

Cho dãy số $(u_{n})$ xác định bởi :

$\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} + n^{2}, n \geq 1 \end{cases}$

Công thức của $u_{n + 1}$ theo n là:

A. $1 + \frac{n (n + 1) (2 n + 1)}{6}$

B. $\frac{n (n + 1) (2 n + 1)}{6}$

C. $\frac{n^{2} {(n + 1)}^{2}}{4}$

D. $1 + \frac{n^{2} {(n + 1)}^{2}}{4}$

Xem đáp án

u1 = 1

u2 = 1 + 12

u3 = 1 + 12 + 22

u4 = 1 + 12 + 22 + 32

...

Đáp án A

Câu 6:

Cho dãy số $(v_{n})$ xác định bởi :

$\{\begin{cases} v_{1} = 3 \\ v_{n + 1} = {v^{2}}_{n}, n \geq 1 \end{cases}$

Khi đó $v_{11}$ bằng

A. $3^{11}$

B. $3^{1024}$

C. $3^{3^{2}}$

D. $3^{22}$

Xem đáp án

$\begin{array}{l} v_{1} = 3 = 3^{2^{0}} \\ v_{2} = 3^{2} = 3^{2^{1}} \\ v_{3} = 3^{4} = 3^{2^{2}} \\ v_{4} = 3^{8} = 3^{2^{3}} \\ ... \\ v_{n} = 3^{2^{n - 1}} \end{array}$

Suy ra: $v_{11} = 3^{2^{10}} = 3^{1024}$

Đáp án là B

Câu 7:

Cho dãy số $u_{n} = n^{2} - 4 n + 7$ . Kết luận nào đúng?

A. Dãy ( $u_{n}$ ) bị chặn trên

B. Dãy ( $u_{n}$ ) bị chặn dưới

C. Dãy ( $u_{n}$ ) bị chặn

D. Các mệnh đề A,B,C đều sai

Xem đáp án

un = n2 – 4n + 7 = (n -2)2 + 3 ≥ 3

⇒(un) bị chặn dưới bởi 3

(un) không bị chặn trên bởi vì n càng lớn thì un càng lớn

Đáp án là B

Câu 8:

Cho dãy số $z_{n} = 1 + (4 n - 3) . 2^{n}$

A. Dãy $z_{n}$ là dãy tăng

B. Dãy $z_{n}$ bị chặn dưới

C. Cả A và B đề sai

D. Cả A và B đều đúng

Xem đáp án

$z_{n + 1} = 1 + (4 n + 1) {.2}^{n + 1}$

$z_{n} = 1 + (4 n - 3) {.2}^{n}$

Xét hiệu

$z_{n + 1} - z_{n} = 1 + (4 n + 1) {.2}^{n + 1} - (1 + (4 n - 3) {.2}^{n})$

$= (8 n + 2) {.2}^{n} - (4 n - 3) {.2}^{n}$

$= (4 n + 5) {.2}^{n} > 0$ $\forall n \in ℕ^{*}$

Suy ra $(z_{n})$ tăng, hơn nữa $z_{n} \geq z_{1} = 3 \forall n \in ℕ^{*}$

Vậy $(z_{n})$ tăng và bị chặn dưới.

Chọn đáp án D.

Câu 9:

Cho x≠0 và x +1/x là một số nguyên. Khi đó với mọi số nguyên dương n, có kết luận gì về $T (n, x) = x^{n} + \frac{1}{x^{n}}$

A. T(n,x) là số vô tỉ

B. T(n,x) là số không nguyên

C. T(n,x) là số nguyên

D. Các kết luận trên đều sai

Xem đáp án

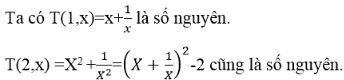
Ta sẽ chứng minh T(n,x) là số nguyên

Thật vậy, áp dụng phép chứng minh quy nạp, Ta có:

Bước cơ sở: T(1,x) là số nguyên. Khẳng định đúng với n=1

Bước quy nạp: Giả sử T(n,x) là số nguyên với mọi n≥1. Ta sẽ chứng minh T(n+1,x) cũng là số nguyên

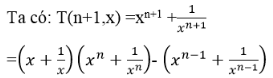
=T(1,x).T(n,x) – T(n-1,x).

Theo giả thuyết quy nạp, Ta có T(1,x),T(n,x), T(n-1,x) là các số nguyên nên T(n+1,x) là số nguyên

Chọn C

Câu 10:

Cho dãy số $(u_{n})$ với $\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = n . u_{n} \end{cases}$ với mọi $n \geq 1$ . Khi đó số hạng thứ 5 của dãy $u_{n}$ là

A. 10

B. 48

C. 16

D. 6

Xem đáp án

Chọn B

Ta có

$u_{2} = u_{1} = 2 u_{3} = 2 u_{2} = 2.2 = 4 u_{4} = 3 u_{3} = 3.4 = 12 u_{5} = 4 u_{4} = 4.12 = 48$

Câu 11:

Cho dãy số: $u_{n} = \frac{\sin (\frac{n π}{3})}{n + 1}$ với mọi n≥1. Khi đó số hạng $u_{3 n}$ của dãy $(u_{n})$ là:

A. $\frac{1}{3 n + 1}$

B. $\frac{1}{n + 1}$

C. $\frac{- 1}{3 n + 1}$

D. $0$

Xem đáp án

Chọn D

Câu 12:

Cho dãy $u_{n} = \frac{n^{2}}{3^{n}}$ với mọi n≥1. Khi đó số hạng $u_{2 n}$ của dãy $u_{n}$ là:

A. $\frac{2 n^{2}}{3^{n}}$

B. $\frac{4 n^{2}}{6^{n}}$

C. $\frac{4 n^{2}}{9^{n}}$

D. $\frac{2 n^{2}}{6^{n}}$

Xem đáp án

Chọn C

Ta có: $u_{2 n} = \frac{{(2 n)}^{2}}{3^{2 n}} = \frac{4 n^{2}}{9^{n}}$

Câu 13:

Cho dãy số $(u_{n})$ : $\{\begin{cases} u_{0} = 1, u_{1} = 3 \\ u_{n + 1} = 4 u_{n} - 3 u_{n - 1} \end{cases} v ớ i m ọ i n \geq 1$

Công thức của số hạng tổng quát của dãy số là:

A. $u_{n} = 2 n^{2} + 1$

B. $u_{n} = 3^{n}$

C. $u_{n} = 2 n + 1$

D. $u_{n} = (n + 5) / (n + 1)$

Xem đáp án

Chọn B

Dự đoán ta được $u_{n} = 3^{n}$

Bằng phương pháp quy nạp ta chứng minh được công thức trên.

Vậy $u_{n} = 3^{n}$

Câu 14:

Cho dãy số $(u_{n})$ : $\{\begin{cases} u_{0} = u_{1} = 1 \\ u_{n + 1} = 4 u_{n} - 4 u_{n - 1} \end{cases} v ớ i m ọ i n \geq 1$

công thức của số hạng tổng quát của dãy số là

A. $u_{n} = 1$

B. $u_{n} = 2^{n} - n . 2^{n - 1}$

C. $u_{n} = - n^{2} + n + 1$

D. $u_{n} = \frac{n^{2} + 2 n + 3}{3 (n + 1)}$

Xem đáp án

Chọn B $\{\begin{cases} u_{0} = u_{1} = 1 \\ u_{n + 1} = 4 u_{n} - 4 u_{n - 1} \end{cases} v ớ i m ọ i n \geq 1$

Ta chứng minh phương án C đúng .

Ta có:

$4 . (2^{n} - n . 2^{n - 1}) - 4 . (2^{n - 1} - (n - 1) . 2^{n - 2} = 4 . 2^{n} - 4 n . 2^{n - 1} - 4 . 2^{n - 1} + 4 (n - 1) . 2^{n - 2} = 2 . 2^{n + 1} - 2 n . 2^{n} - 2^{n + 1} + (n - 1), 2^{n} = 2^{n + 1} - (n - 1) . 2^{n}$

$\Rightarrow u_{n} = 2^{n} - n . 2^{n - 1}$

Câu 15:

Cho dãy số $(u_{n}) : u_{n} = \cos (\frac{2 n + 1}{2} π)$

Khi đó khẳng định nào dưới đây là đúng?

A. $u_{n}$ là dãy đơn điệu tăng

B. $u_{n}$ là dãy đơn điệu giảm

C. $u_{n}$ là dãy không đổi

D. đáp án khác

Xem đáp án

Chọn C

Ta có:

$u_{n} = \cos (\frac{2 n + 1}{2} π) = \cos (\frac{π}{2} + n π) = 0$

∀n≥1 nên ( $u_{n}$ ) là dãy số không đổi

Câu 16:

Cho dãy số $(u_{n}) : u_{1} = \frac{1}{2}; u_{n + 1} = \frac{u_{n}}{n + 1}$

Khi đó khẳng định nào dưới đây là đúng?

A. $u_{n}$ là dãy đơn điệu tăng

B. $u_{n}$ là dãy đơn điệu giảm

C. $u_{n}$ là dãy không đổi

D. đáp án khác

Xem đáp án

Chọn B

Từ giả thiết, suy ra: $u_{n} > 0 \forall n$

Ta có:

$u_{n + 1} - u_{n} = \frac{u_{n}}{n + 1} - u_{n} = u_{n} (\frac{1}{n + 1} - 1) = u_{n} . \frac{- n}{n + 1} < 0$

∀n≥1 nên ( $u_{n}$ ) là dãy số giảm

Câu 17:

Xét dãy $(u_{n})$ : $u_{n} = n + \frac{1}{n}$

khi đó số α dương lớn nhất thoả mãn $u_{n} \geq α \forall n \geq 1$ là:

A. α=1

B. α=2

C. α=1/2

D. $α = \sqrt{2}$

Xem đáp án

Chọn B

Áp dụng bất đẳng thức Cô si ta có:

$u_{n} = n + \frac{1}{n} \geq 2 . \sqrt{n . \frac{1}{n}} = 2$

$\Rightarrow α = 2$

Câu 18:

Xét dãy $u_{n} : u_{n} = \sqrt{n + 100} + \sqrt{100 - n}$

với n là các số tự nhiên nhỏ hơn hoặc bằng 100, số α dương nhỏ nhất thoả mãn $u_{n} \leq α$ là

A. α=10

B. $α = 10 \sqrt{2}$

C. α=11

D. α=20

Xem đáp án

Chọn D

Ta có : $u_{n} = \sqrt{100 + n} + \sqrt{100 - n}$

Áp dụng bất đẳng thức Bunhiacopxki với bộ hai số (1;1) và $(\sqrt{100 + n}; \sqrt{100 - n})$

$1. \sqrt{100 + n} + 1. \sqrt{100 - n} \leq \sqrt{2. (100 + n + 100 - n)} = 20, \forall n \geq 1$

Suy ra $α = 20$

Câu 19:

Cho các dãy số $(u_{n}), (v_{n}), (x_{n}), (y_{n})$ lần lượt xác định bởi:

$u_{n} = \sqrt{n^{2} + 1}, v_{n} = n + \frac{1}{n}, x_{n} = 2^{n} + 1, y_{n} = \frac{n}{n + 1}$

Trong các dãy số trên có bao nhiêu dãy bị chặn dưới

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn D

Trắc nghiệm Phương pháp quy nạp toán học - Dãy số có đáp án

Trắc nghiệm Đại số và Giải tích 11 Bài 1-2: Phương pháp quy nạp toán học - Dãy số

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương