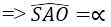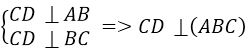14 câu hỏi trắc nghiệm thuộc Trắc nghiệm Mặt phẳng vuông góc có đáp án

Câu 1:

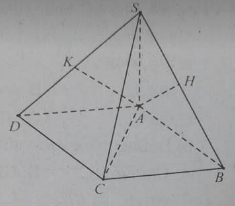
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.

Hai mặt phẳng (SAB) và (SBC) vuông góc vì.

A. Góc của (SAB) và (SBC) là góc ABC và bằng $90^{o}$ .

B. Góc của (SAB) và (SBC) là góc BAD và bằng $90^{o}$ .

C. AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC)

D. BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA

Xem đáp án

Phương án A sai vì AB và CB không vuông góc với giao tuyến SB của (SAB) và (SBC), nên góc ABC không phải là góc của hai mặt phẳng này.

Phương án B sai vì góc BAD không phải là góc của hai mặt phẳng (SAB) với mặt phẳng (SBC)

Phương án C sai vì AB ⊥ BC thì chưa đủ để kết luận AB vuông góc với mặt phẳng (SBC)

Phương án D đúng vì : BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA ⇒ (SBC) ⊥ (SAB)

Đáp án D

Câu 2:

Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.

Hai mặt phẳng (SAC) và (AHK) vuông góc vì:

A. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD)

B. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK)

C. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK)

D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)

Xem đáp án

* Phương án A sai vì hai điều kiện AH ⊥ (SBC) (do AH ⊥ SB và AH ⊥ BC) và AK ⊥ (SCD) (do AK vuông góc với SD và AK ⊥ CD) chưa liên quan đến (SAC);

*Phương án B đúng

Ta có: AH ⊥(SBC) ( vì $A H ⊥ S B; A H ⊥ B C)$ nên $A H ⊥ S C$ (1)

và AK ⊥ (SCD) ( vì $A K ⊥ S D; A K ⊥ D C$ ) nên $A K ⊥ S C$ (2)

Từ (1) và (2) suy ra: SC ⊥ (AHK)

Từ đó suy ra hai mặt phẳng (AHK) và (SAC) vuông góc.

+Phương án C và D đều sai vì chưa đủ điều kiện kết luận SC ⊥ (AHK)

Đáp án B

Câu 3:

Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc.

DE bằng:

A. a√3

B. a√2

C. $3 a^{2}$

D. a(1 + √3)

Xem đáp án

EB ⊥(ABCD) vì nó vuông góc với giao tuyến AB của hai mặt phẳng vuông góc đã cho

⇒ CD ⊥ (EBC) $\Rightarrow C D ⊥ C E$

⇒ tam giác ECD vuông tại C.

$\Rightarrow D E = \sqrt{E C^{2} + C D^{2}}$ (Áp dụng định lý Py - ta - go)

Ta có: EB $⊥$ BC nên tam giác EBC vuông tại B

Suy ra $E C = \sqrt{B E^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$

Nên ta có: $D E = \sqrt{E C^{2} + C D^{2}} = \sqrt{{(a \sqrt{2})}^{2} + a^{2}} = a \sqrt{3}$

⇒ DE = a√3.

Vậy phương án A đúng

Câu 4:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝

Tan của góc giữa mặt bên và mặt đáy bằng:

A. $\tan α$

B. $c o t α$

C. $\sqrt{2} \tan α$

D. $\frac{\sqrt{2}}{2 \tan α}$

Xem đáp án

Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)

Đáp án C

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

Mặt phẳng (ABCD) vuông góc với mặt phẳng:

A. (SAD)

B. (SBD)

C. (SDC)

D. (SBC)

Xem đáp án

Gọi I là giao điểm của AC và BD.

Từ S vẽ SO ⊥ (ABCD)

⇒ OA = OB = OC (là hình chiếu của các đường xiên bằng nhau)

⇒ O là tâm đường tròn ngoại tiếp tam giác ABC

Ta có: BI là đường trung tuyến của tam giác ABC nên O nằm trên đường thẳng BI hay

Vậy: SO ⊂ (SBD) và SO ⊥(ABCD) ⇒ (SBD) ⊥(ABCD)

Đáp án B

Câu 6:

Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng $60^{o}$ . Gọi M và N lần lượt là trung điểm của AB và CD.

Góc giữa hai mặt phẳng (ACD) và (BCD) là:

A. $\overset{⏜}{A C B}$

B. $\overset{⏜}{A N B}$

C. $\overset{⏜}{A D B}$

D. $\overset{⏜}{M N B}$

Xem đáp án

Hai mặt phẳng ( ACD) và ( BCD) cắt nhau theo giao tuyến CD.

Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân tại A

⇒ BN ⊥ CD và AN ⊥ CD

⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)

Đáp án B

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là vuông cạnh a và SA = SB = SC = SD = a.

Góc giữa mặt bên ( SBC) và mặt phẳng đáy có tang bằng:

A. 1

B. $\sqrt{3}$

C. $\frac{\sqrt{3}}{2}$

D. Đáp án khác

Xem đáp án

Gọi O là giao điểm của AC và BD

Từ O kẻ $O M ⊥ B C$ , suy ra: M là trung điểm của BC

Hai mp (SBC) và mp(ABCD) cắt nhau theo giao tuyến là BC

Vì SB = SC nên tam giác SBC cân tại S nên SM vuông góc BC.

Do đó, góc giữa mặt bên ( SBC) với mp (ABCD ) là góc SMO

$O M = \frac{A B}{2} = \frac{a}{2}$

Tam giác SBC có SB = SC = BC nên là tam giác đều cạnh a

Do đó, đường cao $S M = \frac{a \sqrt{3}}{2}$

Ta có: OA = OB = OC = OD và SA= SB = SC = SD nên $S O ⊥ (A B C D)$

Áp dụng định lí Pytago vào tam giác vuông SOM có:

$S O = \sqrt{S M^{2} - O M^{2}} = \sqrt{\frac{3 a^{2}}{4} - \frac{a^{2}}{4}} = \frac{a \sqrt{2}}{2}$

$\tan \hat{S M O} = \frac{S O}{O M} = \frac{\frac{a \sqrt{2}}{2}}{\frac{a}{2}} = \sqrt{2}$

Đáp án D

Câu 8:

Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng $60^{o}$ . Gọi M và N lần lượt là trung điểm của AB và CD.

Mặt phẳng (BCD) vuông góc với mặt phẳng

A. (CDM)

B. (ACD)

C. (ABN)

D. (ABC)

Xem đáp án

Ta có: AC = AD nên tam giác ACD cân tại A $\Rightarrow A N ⊥ C D$ (1)

Tam giác ABD có AB = AD; $\hat{B A D} = 60^{0}$ nên là tam giác đều: BD = AB = AD (2)

Tương tự: tam giác ABC đều: AB = AC = BC (3)

Từ (2 ) và (3) suy ra: BC = BD nên tam giác BCD cân tại B.

$\Rightarrow B N ⊥ C D$ (4)

Từ (1) và (4) suy ra: CD ⊥ (ABN) ⇒ (BCD) ⊥ (ABN)

Đáp án C

Câu 9:

Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.

Khằng định nào sau đây đúng?

A. AB ⊥ (ACD).

B. BC ⊥ (ACD).

C. CD ⊥ (ABC).

D. AD ⊥ (BCD).

Xem đáp án

Phương án A sai vì chỉ có AB ⊥ CD; phương án B sai vì chỉ có : BC ⊥ CD

Phương án C đúng vì

Phương án D sai vì AD không vuông góc với đường thẳng nào thuộc mặt phẳng (BCD)

Đáp án C

Câu 10:

Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:

A. trung điểm J của AB

B. trung điểm I của BC

C. trung điểm K của AD

D. trung điểm M của CD

Xem đáp án

CD ⊥ (ABC) vì CD ⊥ AB và CD ⊥ BC

AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD

Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C

Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của BC không cách đều ba điểm A, B, C

Phương án C đúng vì :

Tam giác ABD vuông tại B có BK là đường trung tuyến nên: $B K = A K = D K = \frac{A D}{2}$ (1)

Tam giác ACD vuông tại C có CK là đường trung tuyến ứng với cạnh huyền AD nên:

$C K = A K = D K = \frac{A D}{2}$ (2)

Từ (1).(2) suy ra: AK = BK = CK = DK

Do đó ,điểm K cách đều 4 điểm A; B; C; D.

Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D.

Đáp án C

Câu 11:

Cho chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.

Đường thẳng SA vuông góc với

A. SC

B. SB

C. SD

D. CD

Xem đáp án

Tứ giác ABCD là hình vuông nên $A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$

Tam giác SAC có SA = a, SC = a và AC = a√2

Ta thấy: $S A^{2} + S C^{2} = A C^{2}$

⇒ SAC là tam giác vuông tại S, hay SA ⊥ SC

Đáp án A

Câu 12:

Cho hình lập phương ABCD.A’B’C’D’:

Mặt phẳng (ACC’A’) Không vuông góc với.

A. (ABCD)

B. (CDD’C’)

C. (BDC’)

D. (A’BD)

Xem đáp án

Ta có: $\{\begin{matrix} B D ⊥ A C \\ B D ⊥ A A ' \end{matrix} \Rightarrow B D ⊥ (A C C' A')$

* Vì $B D \subset (A B C D) \Rightarrow (A B C D) ⊥ (A C C' A')$

* Vì $B D \subset (B D C') \Rightarrow (B D C') ⊥ (A C C' A')$

* Vì $B D \subset (A' B D) \Rightarrow (A' B D) ⊥ (A C C' A')$

Vậy mp(CDD’C’) không vuông góc với mặt phẳng (ACC’A’).

Chọn B.

Câu 13:

Cho hình lập phương ABCD.A’B’C’D’: Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:

A. trung điểm của BD

B. trung điểm của A’B

C. trung điểm của A’D

D. tâm của tam giác BDA’

Xem đáp án

Ta có: BD = A’B = A’D nên tam giác A’BD là tam giác đều.

Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.

Đáp án D

Câu 14:

Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc.

Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?

A. Không vuông góc với mặt nào?

B. (ACD)

C. (ABC)

D. (BCD)

Xem đáp án

Ta có: $\begin{array}{l} A B ⊥ B C \\ A B ⊥ C D \end{array}\} \Rightarrow A B ⊥ (B C D)$

Mà $A B \subset (A B D)$

Do đó $(A B D) ⊥ (B C D)$ .

Đáp án D

Trắc nghiệm Mặt phẳng vuông góc có đáp án

Trắc nghiệm Mặt phẳng vuông góc có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương