Trắc nghiệm Đại số và Giải tích 11 Bài 1 (Có đáp án): Quy tắc đếm
Trắc nghiệm Đại số và Giải tích 11 Bài 1 (Có đáp án): Quy tắc đếm
-
76 lượt thi
-
18 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Một lớp có 23 học sinh nữ và 17 học sinh nam.
Hỏi có bao nhiêu cách chọn một học sinh tham gia cuộc thi tìm hiểu môi trường?
 Xem đáp án
Xem đáp án
Theo quy tắc cộng có: 23 +17 = 40 cách chọn một học sinh tham gia cuộc thi môi trường.
Vì vậy chọn đáp án C
Nhận xét: học sinh có thể đọc không kĩ đề:
chọn 1 học sinh nữ trong 23 học sinh nữ nên có 23 cách chọn (phương án A);
hoặc chọn một học sinh nam trong số 17 học sinh nam nên có 17 cách chọn (phương án B);
hoặc nhầm sang quy tắc nhân nên có 23 .17 = 391 cách chọn
Đáp án đúng C
Câu 2:
Một lớp có 23 học sinh nữ và 17 học sinh nam.
Hỏi có bao nhiêu cách chọn hai học sinh tham gia hội trại với điều kiện có cả nam và nữ?
 Xem đáp án
Xem đáp án
*Việc chọn hai học sinh (nam và nữ) phải tiến hành hai hành động liên tiếp
Hành động 1: chọn 1 học sinh nữ trong số 23 học sinh nữ nên có 23 cách chọn
Hành động 2: chọn 1 học sinh nam nên có 17 cách chọn
Theo quy tắc nhân, có 23*17=391 cách chọn hai học sinh tham gia hội trại có cả nam và nữ.
Vì vậy chọn phương án B
* Nhận xét: học sinh có thể nhầm:
- Dùng quy tắc cộng để cộng 23 +17 =40 cách (phương án A)
- Có thể nhầm sang bài toán chọn hai học sinh trong 40 học sinh, nên có cách chọn (phương án C)
- Có thể nhầm khi suy luận.
Chọn 1 học sinh trong 40 học sinh nên có 40 cách.
Chọn 1 học sinh trong số 40 -1 = 39 học sinh còn lại nên có 39 cách.
Theo quy tắc nhân ta có : 40 . 39 =1560 cách chọn
Đáp án đúng B
Câu 3:
Một túi có 20 viên bi khác nhau trong đó có 7 bi đỏ, 8 bi xanh và 5 bi vàng
Số cách lấy 3 viên bi khác màu là
 Xem đáp án
Xem đáp án
* Việc chọn 3 viên bi khác màu phải tiến hành 3 hành động liên tiếp:
chọn 1 bi đỏ trong 7 bi đỏ nên có 7 cách chọn,
tương tự có 8 cách chọn 1 bi xanh và 5 cách chọn 1 bi vàng.
Theo quy tắc nhân ta có: 7*8*5 = 280 cách.
Vậy đáp án là B
Nhận xét: học sinh có thể nhầm:
- Sử dụng quy tắc cộng để có: 7 +8 +5 = 20 cách (phương án A)
Chọn 3 viên bi trong 20 viên bi nên có =1140 cách (phương án D)
- Hoặc chọn thứ tự 3 viên bi trong 20 viên bi nên có: 20.19.18=6840 cách (phương án C)
Đáp án đúng B
Câu 4:
Một túi có 20 viên bi khác nhau trong đó có 7 bi đỏ, 8 bi xanh và 5 bi vàng.
Số cách lấy 2 viên bi khác màu là:
 Xem đáp án
Xem đáp án
Muốn lấy được 2 viên bi khác màu từ trong túi đã cho xảy ra các trường hợp sau:
Trường hợp 1- Lấy 1 bi đỏ và 1 bi xanh:
có 7 cách để lấy 1 bi đỏ và 8 cách để lấy 1 bi xanh. Do đó có 7.8 =56 cách lấy
-Trường hợp 2. Lấy 1 bi đỏ và 1 bi vàng:
có 7 cách lấy 1 bi đỏ và 5 cách lấy 1 bi vàng.
Do đó có 7.5=35 cách lấy
- trường hợp 3.Lấy 1 bi xanh và 1 bi vàng:
có 8 cách để lấy 1 bi xanh và 5 cách để lấy 1 bi vàng.
Do đó có 8.5 = 40 cách để lấy
- Áp dụng quy tắc cộng cho 3 trường hợp, ta có 56 + 35 +40 = 131 cách
Vì vậy chọn đáp án là C
Nhận xét: học sinh có thể nhầm
- Coi việc lấy hai viên bi khác màu không là hành động liên tiếp, nên đã sử dụng quy tắc cộng (7+8) + (8+5) + (5+7) = 40 cách lấy (phương án A)
- Nhầm lẫn giữa quy tắc cộng và quy tắc nhân nên cho kết quả là: (7+8).(8+5).(5+7)= 15.13.12=2340 cách (phương án D)
- Coi 3 trường hợp lấy 2 viên bi khác màu là ba hành động liên tiếp, nên đã sử dụng quy tắc nhân 56.35.40 = 78400 cách (phương án B)
Đáp án đúng là C
Câu 5:
Từ các số 0,1,2,3,4,5 có thể lập được:
Bao nhiêu số có hai chữ số khác nhau và chia hết cho 5?
 Xem đáp án
Xem đáp án
Gọi tập hợp E = {0,1,2,3,4,5}
Số tự nhiên có hai chữ số khác nhau có dạng:
Với b = 0 thì có 5 cách chọn a ( vì a ≠ 0)
Với b = 5 thì có 4 cách chọn a ( vì a ≠ b và a ≠ 0)
Theo quy tắc cộng, có tất cả 5 + 4 = 9 số tự nhiên cần tìm.
Chọn đáp án là C.
Câu 6:
Từ các số 0,1,2,3,4,5 có thể lập được: Bao nhiêu số có 3 chữ số khác nhau chia hết cho 3?
 Xem đáp án
Xem đáp án
Gọi tập hợp E = {0,1,2,3,4,5}
* Số tự nhiên có ba chữ số khác nhau có dạng
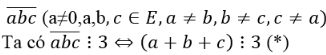
Trong E có các bộ chữ số thoả mãn (*) là: (0,1,2);(0,1,5);(0,2,4);(1,2,3);(1,3,5);(2,3,4);(3,4,5)
Mỗi bộ gồm ba chữ số khác nhau và khác 0 nên ta viết được 3.2.1 =6 số có ba chữ số chia hết cho 3
Mỗi bộ gồm ba chữ số khác nhau và có một chữ số 0 nên ta viết được 2.2.1 = 4 số có ba chữ số chia hết cho 3
Vậy theo quy tắc cộng ta có: 6.4 +4.3 =36 số có 3 chữ số chia hết cho 3 Chọn đáp án là A
Nhận xét :
- Học sinh có thể nhầm áp dụng quy tắc nhân cho kết quả: 64 .43 = 82944 số (phương án C)
- Học sinh có thể không để ý điều kiên a≠0 nên cho kết quả 6.7 =42 (phương án B)
- Học sinh có thể liệt kê bộ ba chữ số thoả mãn (*) còn thiếu nên không thể cho các kết quả A,B,C (phương án D)
ĐÁP ÁN A
Câu 7:
Từ các số 0,1,2,3,4,5 có thể lập được:
Bao nhiêu số có ba chữ số ( không nhất thiết khác nhau) và là số chẵn?
 Xem đáp án
Xem đáp án
Gọi tập hợp E = {0,1,2,3,4,5}
Số tự nhiên có 3 chữ số có dạng
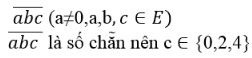
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)
ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)
Áp dụng quy tắc nhân ta có 3.6.5 = 90 số có 3 chữ số.
Vì vậy đáp án là B
Câu 8:
Cho dãy với mỗi chỉ nhận giá trị 0 hoặc 1. Hỏi có bao nhiêu dãy như vậy?
 Xem đáp án
Xem đáp án
Chọn B
Mỗi ai chỉ nhận hai giá trị (0 hoặc 1).
Như vậy, có 2 cách chọn
Tương tự; mỗi số có 2 cách chọn
Theo quy tắc nhân số dãy a1, a2, a3, a4, là 2×2×2×2=16
Câu 9:
Trong một lớp học có 20 học sinh nam và 24 học sinh nữ. Giáo viên chủ nhiệm cần chọn 2 học sinh; 1 nam và 1 nữ tham gia đội cờ đỏ. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Chọn C
Có 20 cách chọn 1 bạn học sinh nam và 24 cách chọn 1 bạn học nữ.
Vậy có 20×24= 480 cách chọn hai bạn (1 nam, 1 nữ) tham gia đội cờ đỏ
Câu 10:
Trên giá sách có 5 quyển sách Tiếng Anh khác nhau, 6 quyển sách Toán khác nhau và 8 quyển sách Tiếng Việt khác nhau. Số cách chọn 1 quyển sách là:
 Xem đáp án
Xem đáp án
Có 5 cách chọn 1 quyển sách Tiếng Anh.
Có 6 cách chọn 1 quyển sách Toán
Và 8 cách chọn 1 quyển sách Tiếng Việt
Số cách chọn một quyển sách là 5+6+8=19
Chọn A
Câu 11:
Trên giá sách có 5 quyển sách Tiếng Anh khác nhau, 6 quyển sách Toán khác nhau và 8 quyển sách Tiếng Việt khác nhau. Số cách chọn 3 quyển sách khác môn học là:
 Xem đáp án
Xem đáp án
Có 5 cách chọn 1 quyển sách Tiếng Anh
Có 6 cách chọn 1 quyển sách Toán
và 8 cách chọn 1 quyển sách Tiếng Việt
Số cách chọn 3 quyển sách có đủ 3 loại là 5×6×8=240
Chọn B
Câu 12:
Trên giá sách có 5 quyển sách Tiếng Anh khác nhau, 6 quyển sách Toán khác nhau và 8 quyển sách Tiếng Việt khác nhau. Số cách chọn 2 quyển sách khác môn học là:
 Xem đáp án
Xem đáp án
+ Trường hợp 1: chọn 1 tiếng anh và 1 toán có 5.6 = 30 cách
+ Trường hợp 2. Chọn 1 tiếng anh và 1 tiếng việt có 5.8 = 40 cách
+ Trường hợp 3. Chọn 1 toán và 1 tiếng việt có 6.8 = 48 cách
Số cách chọn 2 quyển sách khác môn học là: 30 + 40 + 48 =118 cách
Chọn C
Câu 13:
Có bao nhiêu số chẵn có hai chữ số?
 Xem đáp án
Xem đáp án
Số chẵn có hai chữ số có dạng : với a≠0, b chẵn.
Có 9 cách chọn a( từ 1 đến 9)
Có 5 cách chọn b (là 0,2,4,6,8).
Vậy tất cả có 9×5=45 số
Chọn B
Câu 14:
Có bao nhiêu số lẻ có hai chữ số khác nhau?
 Xem đáp án
Xem đáp án
Chọn A
Số lẻ có hai cữ số khác nhau có dạng
với a≠0, a≠b,b lẻ.
Có 5 cách chọn b( là 1,3,5,7,9).
Ứng với mỗi cách chọn b sẽ có 8 cách chọn a( trừ 0 và b).
Theo quy tác nhân có tất cả 5.8=40 số
Câu 15:
Gieo đồng thời 3 con súc sắc. Có bao nhiêu cách để tổng số chấm trên ba con súc sắc xuất hiện bằng 10?
 Xem đáp án
Xem đáp án
Chọn B
Bài toán quy về tìm các số hạng :
với a,b,c ∈{1,2,3,4,5,6} và a+b+c=10.
Nhận thấy 10=1+3+6=1+4+5=2+3+5=2+4+4=3+3+4=2+2+6
*Với 3 chữ số khác nhau , lập được 3.2.1=6 số có 3 chữ số
( chẳng hạn với 1,3,6 lập được 6 số có 3 chữ số là 136,163,361,316,613,631)
*Với ba chữ số trong đó có hai chữ số giống nhau, lập được 3số có 3 chữ số
( chẳng hạn với 2,4,4 lập được 3 số có 3 chữ số là 244,424,442.
Vì vậy, theo quy tắc cộng , ta thu được 6+6+6+3+3+3=27 số
Câu 16:
Cho 6 chữ số 0,1,2,3,4,5. Từ 6 chữ số trên có thể lập được bao nhiêu số, mỗi số có 4 chữ số khác nhau và không chia hết cho 5?
 Xem đáp án
Xem đáp án
Chọn C
Số có bốn chữ số có dạng :
( a≠0,a,b,c,d∈ E={0,1,2,3,4,5})
Do không chia hết cho 5 nên có 4 cách chọn d( là 1,2,3,4)
Chọn a ∈ E\{0,d} nên có 4 cách chọn a
Chọn b ∈ E\{a,d} nên có 4 cách chọn b
Chọn c ∈ E\{a,b,d} nên có 3 cách chọn c
Theo quy tắc nhân, có 4. 4. 4. 3=192 số
Câu 17:
Số 2016 có bao nhiêu ước số nguyên dương?
 Xem đáp án
Xem đáp án
, nên mỗi ước số nguyên dương của 2016 có dạng
( với m,n,p ∈ N và 0≤ m ≤ 5, 0 ≤ n ≤2, 0 ≤ p ≤1
Do đó, có 6 cách chọn m,3 cách chọn n, 2 cách chọn p.
Theo quy tắc nhân , có 6. 3. 2=36 ước số nguyên dương của 2016
Nhận xét. Tổng quát A= p1k1p2k2…pnkn với (p1,p2,…,pn là các nguyên tố khác nhau) sẽ có (k1+1)(k2+2)(kn+1) ước số nguyên dương
Chọn B
Câu 18:
Các thành phố A,B,C,D được nối với nhau bằng các con đường như hình vẽ:

Số cách đi từ thành phố A đến D mà qua B và C chỉ có một lần là:
 Xem đáp án
Xem đáp án
+ Đi từ A đến B có 4 cách
+ Đi từ B đến C có 3 cách
+ Đi từ C đến D có 5 cách
Số cách đi từ A đến D (qua B và C chỉ một lần) là 4.3.5=60
Chọn B
