Trắc nghiệm Đại số và Giải tích 11 Bài 2 (Có đáp án): Hoán vị - Chỉnh hợp - Tổ hợp
Trắc nghiệm Đại số và Giải tích 11 Bài 2 (Có đáp án): Hoán vị - Chỉnh hợp - Tổ hợp
-
162 lượt thi
-
20 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Một tổ có 4 học sinh nam và 5 học sinh nữ.
Hỏi có bao nhiêu cách xếp học sinh trong tổ thành một hàng dọc?
 Xem đáp án
Xem đáp án
- Có tất cả : 4 + 5 = 9 học sinh.
- Mỗi cách xếp 9 học sinh thành hàng dọc là một hoán vị của 9 học sinh đó.
Vậy có tất cả 9! Cách xếp.
Chọn đáp án là C
Nhận xét: học sinh có thể nhầm lẫn xếp nam và nữ riêng nên cho kết quả 4!. 5! (phương án A);
hoặc vừa xếp nam và nữ riêng và sử dụng quy tắc cộng để cho kết quả 4!+5! (phương án B);
hoặc chọn 4 học sinh nam trong 9 học sinh và 5 học sinh nữ trong 9 học sinh để cho kết quả A94.A95 ( phương án D)
Câu 2:
Một tổ có 4 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách xếp học sinh trong tổ thành hàng dọc sao cho học sinh nam và nữ đứng xen kẽ nhau?
 Xem đáp án
Xem đáp án
- Nếu đánh số theo hàng dọc từ 1 đến 9 thì cần xếp 5 học nữ vào 5 vị trí lẻ nên có 5!cách xếp;
và xếp 4 học sinh nam vào 4 vị trí chẵn nên có 4!cách xếp.
Theo quy tắc nhân ta có, ta có 4!. 5! Cách xếp 9 học sinh thành hàng dọc xen kẽ nam nữ.
Chọn A
Câu 3:
Từ tập A= {1; 2;3;4; 5; 6; 7; 8; 9}, lập được bao nhiêu số có bốn chữ số?
 Xem đáp án
Xem đáp án
Mỗi số tự nhiên có bốn chữ số khác nhau và khác 0 từ các chữ số của tập E={1,2,3,4,5,6,7,8,9} là một chỉnh hợp chập 4 của 9 phần tử.
Vậy có A94 số cần tìm.
Chọn đáp án B
Câu 4:
Từ tập A={0;1;2;3;4;5;6;7;8;9}, lập được bao nhiêu số có 4 chữ số khác nhau.
 Xem đáp án
Xem đáp án
* Gọi số có bốn chữ số khác nhau là ¯abcd
Do a ∈ {1,2,3,4,5,6,7,8,9} nên có 9 cách chọn a.
Ứng với mỗi cách chọn a, còn 10 -1 =9 chữ số để viết ¯bcd (b có thể bằng 0),
Mỗi cách viết ¯bcdlà một chỉnh hợp chập 3 của 9 chữ số,
nên có A93 số ¯bcd
Theo quy tắc nhân, có 9A93 số cần tìm. Chọn đáp án là B.
Câu 5:
Trong mặt phẳng có 18 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác mà các đỉnh của nó thuộc tập hợp các điểm đã cho là:
 Xem đáp án
Xem đáp án
- Chọn 3 điểm trong 18 điểm đã cho làm 3 đỉnh của một tam giác.
Mỗi tam giác là một tổ hợp chập 3 của 18.
Vì vậy số tam giác là C183 (chọn phương án B)
Câu 6:
Trong mặt phẳng có 18 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số vecto có điểm đầu và điểm cuối thuộc tập điểm đã cho là:
 Xem đáp án
Xem đáp án
- Do ![]()
nên mỗi vecto là một chỉnh hợp chập hai của 18.
Vì vậy, số vecto là A182 (chọn đáp án là A)
Câu 7:
Có 5 bì thư khác nhau và có 8 con tem khác nhau. Chọn từ đó ra 3 bì thư và 3 con tem sau đó dán 3 con tem lên 3 bì thư đã chọn. Biết rằng một bì thư chỉ dán 1 con tem. Hỏi có bao nhiêu cách dán?
 Xem đáp án
Xem đáp án
Có 5 bì thư khác nhau, chọn 3 bì thư có C53 cách chọn
Có 8 tem khác nhau, chọn 3 con tem thì có C83 cách chọn
Dán 3 con tem lên 3 bì thư thì có 3!cách dán khác nhau.
Theo quy tắc nhân ta có 3!C53.C83 cách dán 3 con tem lên 3 bì thư (chọn đáp án D)
Nhận xét: học sinh có thể nhầm lẫn: số cách chọn 3 bì thư là A53, số cách chọn 3 con tem là A83 hoặc không tính cách dán 3 con tem lên 3 bì thư dẫn đến có thể chọn các phương án A, B và C.
Chọn D
Câu 9:
Một nhóm học sinh gồm 5 nam và 5 nữ xếp thành một hàng ngang. Tính số cách xếp để cho học sinh nam và học sinh nữ đứng cạnh nhau:
 Xem đáp án
Xem đáp án
Để xếp 5 nam và 5 nữ xếp thành một hàng ngang sao cho học sinh nam và học sinh nữ đứng cạnh nhau thì ta sẽ xếp xen kẽ.
Đánh số 10 vị trí từ 1 đến 10.
+ Trường hợp 1. Nam đứng vị trí lẻ, nữ đứng các vị trí chẵn
có: 5!.
+ Trường hợp 2. Nam đứng vị trí chẵn, nữ đứng các vị trí lẻ
Có
Vậy có tất cả cách xếp nam, nữ đứng xen kẽ thành một hàng ngang
Chọn C
Câu 10:
Có 10 khách được xếp vào một bàn tròn có 10 chỗ. Tính số cách xếp ( 2 cách xếp được coi là như nhau nếu cách này nhận được từ cách kia bằng cách xoay bàn đi một góc)
 Xem đáp án
Xem đáp án
Xếp 1 khách nào đó vào một vị trí bất kì, có một cách xếp.
( Khi xếp vào bàn tròn thì người đầu tiên không quan trọng)
Sau đó xếp 9 khách còn lại vào 9 vị trí còn lại. Có 9! cách xếp .
Theo quy tắc nhân , có 1. 9!=9! Cách xếp
Nhận xét. Tổng quát có (n-1)! Cách xếp n khách vào bàn tròn có n chỗ
Chọn B
Câu 11:
An và Bình cùng 7 bạn khác rủ nhau đi xem bóng đá. 9 bạn được xếp vào 9 ghế và thành hàng ngang. Có bao nhiêu cách xếp chỗ ngồi cho 9 bạn sao cho 2 bạn An và Bình ngồi cạnh nhau?
 Xem đáp án
Xem đáp án
+ Coi 2 bạn An và Bình là 1 phần tử X.
+ Số cách xếp X và 7 bạn khác thành hàng ngang là 8!.
+ Đổi chỗ hai bạn An và Bình cho nhau ta được thêm 1 cách xếp
Do đó, số cách xếp thỏa mãn đầu bài là:
8!. 2= 8. 7!. 2 = 16. 7!
Chọn D
Câu 12:
An và Bình cùng 7 bạn khác rủ nhau đi xem bóng đá. 9 bạn được xếp vào 9 ghế và thành hàng ngang.
Có bao nhiêu cách xếp chỗ ngồi cho 9 bạn sao cho 2 bạn An và Bình không ngồi cùng nhau?
 Xem đáp án
Xem đáp án
* Số cách xếp 9 bạn vào 9 chỗ là 9! Cách.
* Ta tính số cách để An và Bình ngồi cạnh nhau:
Coi 2 bạn An và Bình là 1 phần tử X.
Xếp X và 7 bạn khác thành hàng ngang có 8! cách
Trong X, đổi chỗ An và Bình cho nhau ta được thêm cách xếp
Do đó, số cách xếp 9 bạn thành hàng ngang để An và Bình cạnh nhau là : 2. 8!
* Suy ra, số cách xếp để An và Bình không ngồi cạnh nhau là 9! – 2.8!= 282240
Chọn C
Câu 13:
Có bao nhiêu cách phân chia 8 học sinh ra 2 nhóm: một nhóm có 5 học sinh, nhóm kia có 3 học sinh?
 Xem đáp án
Xem đáp án
Số cách chọn 5 học sinh từ 8 học sinh là .
Sau khi, chọn 5 học sinh này thì còn 3 học sinh khác.
Cho 3 học sinh này phân vào nhóm còn lại: có 1 cách
Vậy sẽ có cách
Chọn B
Câu 14:
Có bao nhiêu cách chọn từ 40 học sinh trong lớp ra 2 bạn vào Đội cờ đỏ, 3 bạn vào Ban Chấp hành Đoàn. Biết một học sinh không cùng làm 2 chức vụ.
 Xem đáp án
Xem đáp án
Chọn 2 bạn trong số 40 bạn vào đội cờ đỏ nên có C402 cách chọn.
Sau khi chọn 2 bạn rồi, chọn 3 trong số 40-2=38 bạn còn lại
vào ban chấp hành đoàn nên có C383 cách chọn.
Theo quy tắc nhân, có C402. C383 cách chọn
Chọn A
Câu 15:
Nam xếp 5 quyển sách Toán khác nhau, 4 quyển sách Hoá khác nhau và 3 quyển sách Lí khác nhau lên giá sách theo từng môn học ( tức là các quyển sách cùng môn xếp cạnh nhau). Hỏi Nam có bao nhiêu cách xếp?
 Xem đáp án
Xem đáp án
Có 3 môn học nên có 3! Cách xếp sách theo môn.
Ứng với mỗi cách xếp theo môn có 5!cách xếp toán,4! Cách xếp hóa và 3! Cách xếp sách lí.
Vậy số cách xếp sách là : 3!5!4!3!cách
Chọn C
Câu 16:
Ban văn nghệ lớp 11A có 7 học sinh nam và 9 học sinh nữ. Cần chọn ra 5 học sinh nam và 5 học sinh nữ để ghép thành 5 cặp nam nữ trình diễn tiết mục thời trang. Hỏi có bao nhiêu cách chọn thoả mãn điều kiện bài toán?
 Xem đáp án
Xem đáp án
Có 7 nam chọn 5 em thì có C75 cách chọn,
Có 9 nữ chọn 5 nữ thì có C95 cách chọn.
Sau đó, ta có 5! Cách ghép 5 nam và 5 nữ đã chọn.
Vậy có C75 . C95 .5!=317520 cách thỏa mãn yêu cầu bài toán.
Nhận xét. Những nhầm lẫn học sinh có thể tính ra kết quả
C75 . C95 =2646 ( phương án A) Do quan niệm ghép 5 nam,5 nữ thành cặp chỉ có một cách.
A75 .A95 =38102400( phương án C) Do quan niệm nhầm việc chọn 5 bạn trong 7 bạn (hoặc trong 9 bạn) là một chỉnh hợp chập 5 của 7( hoặc của 9)
Chọn B
Câu 17:
Một đội thanh niên tình nguyện có 15 người gồm 12 nam và 3 nữ. Hỏi có bao nhiêu cách phân công đội thanh niên tình nguyện đó về giúp đỡ 3 tỉnh miền núi, sao cho mỗi tỉnh có 4 nam và 1 nữ?
 Xem đáp án
Xem đáp án
*Chọn 4 nam và 1 nữ phân về tỉnh thứ nhất có: C31 .C124
* Lúc này, chỉ còn lại 2 nữ và 8 nam. Chọn 4 nam và 1 nữ từ các bạn còn lại để phân về tỉnh thứ hai:
có C21 .C84
* Sau đó, chỉ còn lai j 4 nam và 1 nữ. Phân 4 nam và 1 nữ này vào tỉnh thứ ba.
có C11 .C44 cách
Do đó có C31 .C124 .C21 .C84 . C11 .C44 =207900 cách
Chọn C
Câu 18:
Giải phương trình:
 Xem đáp án
Xem đáp án
Điều kiện x∈N, x≥3
\Ta có:
6( x- 1). (x- 2) - (x - 1). (x-2) = 30
5(x - 1)(x - 2)= 30( x- 1).(x - 2) = 6
Suy ra, x = -1 ( loại) hoặc x = 4
Vậy x = 4
Nhận xét. Học sinh có thể quên đặt điều kiện cho x nên tìm ra 3 nghiệm( x=0,x=-1,x=4)
Chọn B
Câu 20:
Bất phương trình
có tập nghiệm là:
 Xem đáp án
Xem đáp án
Điều kiện n∈N và n≥3. Ta có :
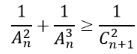
(n- 2). (n + 1 )+ n + 12(n - 1). (n - 2)
Vì n∈N và n≥3 nên n∈{3;4;5}
Chọn D
