Giải SGK Toán 12 KNTT Khảo sát và vẽ đồ thị hàm số với phần mềm Geogebra có đáp án
Giải SGK Toán 12 KNTT Khảo sát và vẽ đồ thị hàm số với phần mềm Geogebra có đáp án
-
30 lượt thi
-
11 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho các hàm số đa thức sau:
(1) ;
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(1) .
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới

Để tính đạo hàm cấp hai ta dùng lệnh Derivative( , 2), kết quả sẽ được hiển thị như hình bên dưới
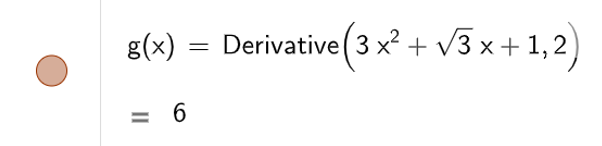
b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum( ), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số vào ô lệnh , màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
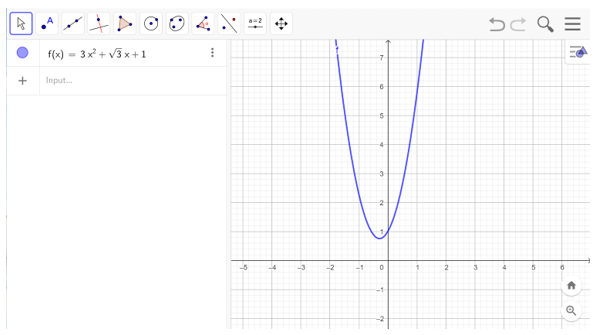
Câu 2:
Cho các hàm số đa thức sau:
(2) y = x3 – 6x2 + 9;
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(2) y = x3 – 6x2 + 9
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative(x3 – 6x2 + 9), kết quả sẽ được hiển thị như hình bên dưới
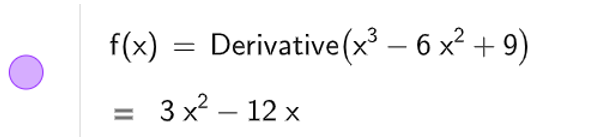
Để tính đạo hàm cấp hai ta dùng lệnh Derivative(x3 – 6x2 + 9, 2), kết quả sẽ được hiển thị như hình bên dưới

b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum(x3 – 6x2 + 9), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số y = x3 – 6x2 + 9 vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
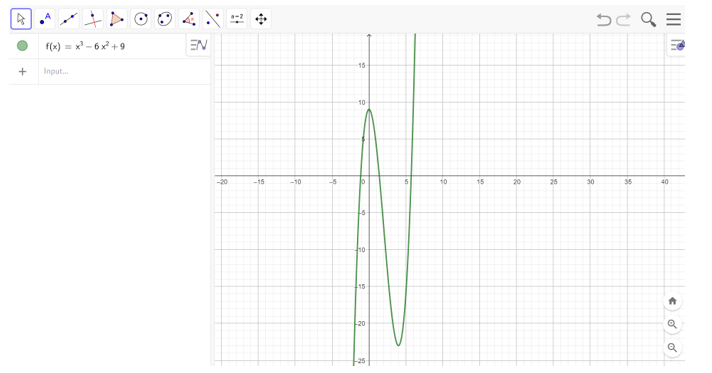
Câu 3:
Cho các hàm số đa thức sau:
(3) y = x4 – 4x2 + 3.
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(3) y = x4 – 4x2 + 3
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative(x4 – 4x2 + 3), kết quả sẽ được hiển thị như hình bên dưới
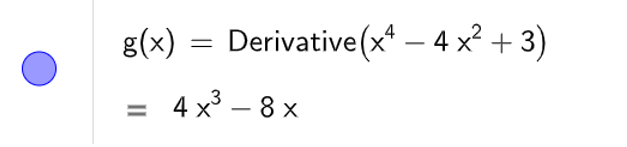
Để tính đạo hàm cấp hai ta dùng lệnh Derivative(x4 – 4x2 + 3, 2), kết quả sẽ được hiển thị như hình bên dưới
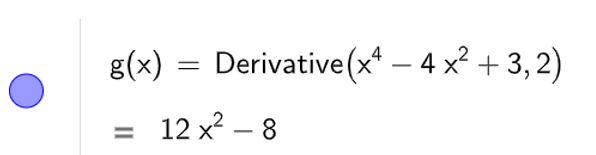
b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum(x4 – 4x2 + 3), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số y = x4 – 4x2 + 3 vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
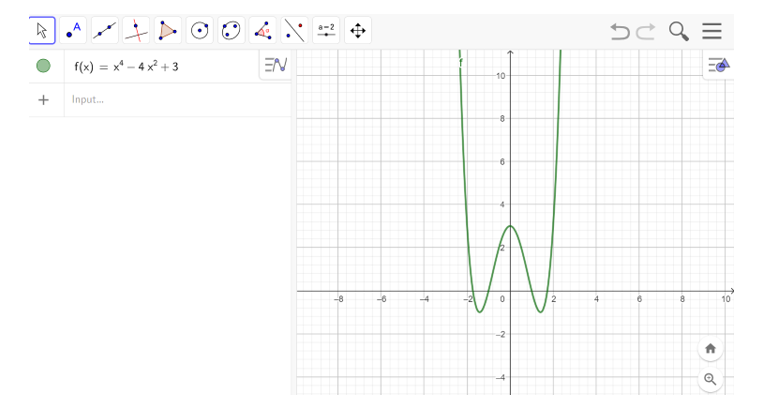
Câu 4:
Cho các hàm số phân thức hữu tỉ sau:
(1) ;
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(1)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
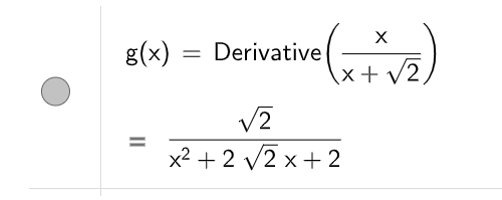
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
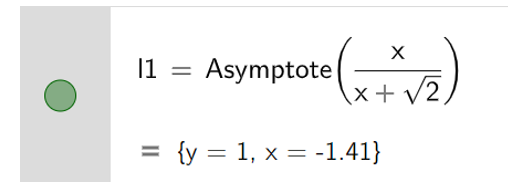
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
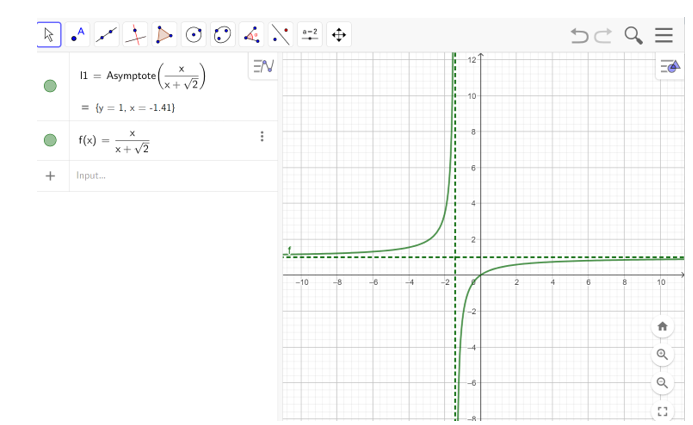
Câu 5:
Cho các hàm số phân thức hữu tỉ sau:
(2) ;
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(2)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
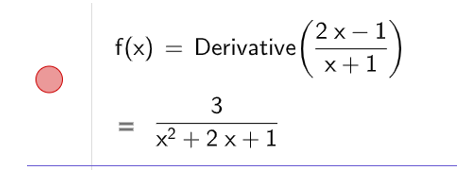
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
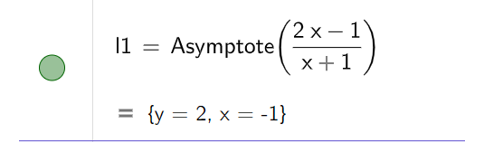
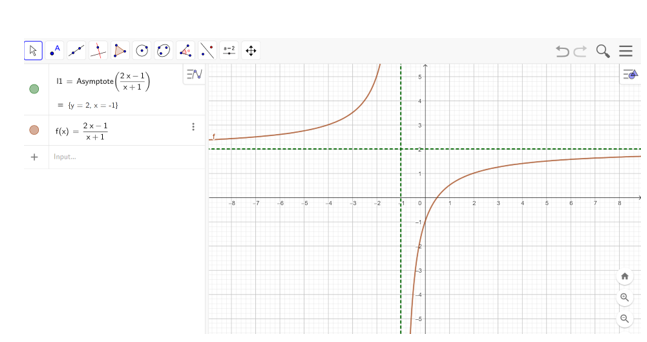
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
Câu 6:
Cho các hàm số phân thức hữu tỉ sau:
(3) ;
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(3)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
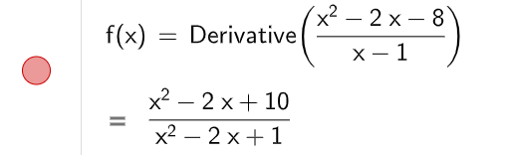
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
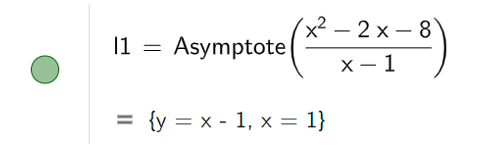
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
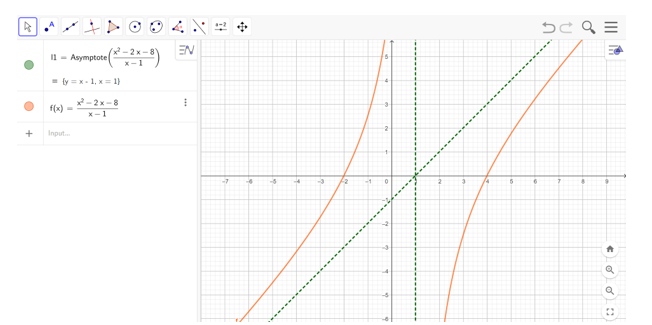
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
Câu 7:
Cho các hàm số phân thức hữu tỉ sau:
4) .
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
 Xem đáp án
Xem đáp án
(4)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
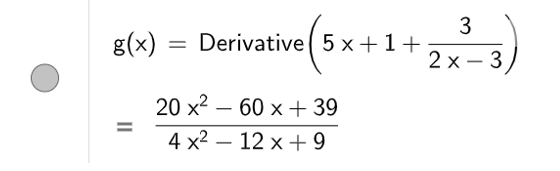
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
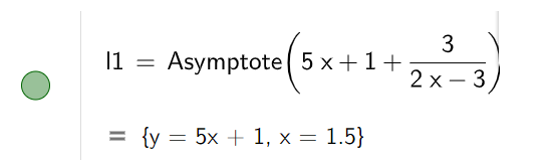
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
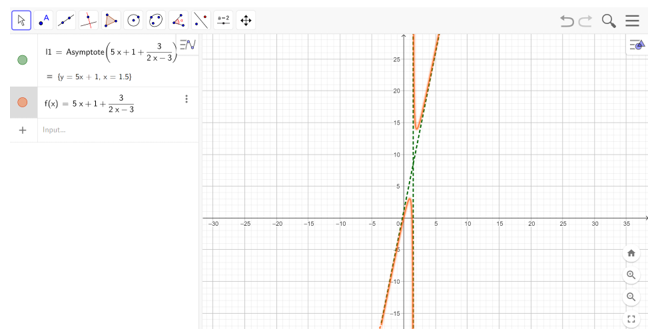
Câu 8:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y = x3 – 3x2 – 9x + 35 trên đoạn [−4; 4];
 Xem đáp án
Xem đáp án
a) Để tìm giá trị lớn nhất của hàm số y = x3 – 3x2 – 9x + 35 trên đoạn [−4; 4] ta dùng lệnh Max(x3 – 3x2 – 9x + 35, −4, 4), kết quả thể hiện ở hình vẽ sau
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: a) y = x3 – 3x2 – 9x + 35 trên đoạn [−4; 4]; (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid25-1712560699.png)
Vậy giá trị lớn nhất của hàm số là 40.
Để tìm giá trị nhỏ nhất của hàm số y = x3 – 3x2 – 9x + 35 trên đoạn [−4; 4] ta dùng lệnh Min(x3 – 3x2 – 9x + 35, −4, 4), kết quả thể hiện ở hình vẽ sau
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: a) y = x3 – 3x2 – 9x + 35 trên đoạn [−4; 4]; (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid26-1712560712.png)
Vậy giá trị nhỏ nhất của hàm số là 8.
Câu 9:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
 Xem đáp án
Xem đáp án
b) Để tìm giá trị lớn nhất của hàm số trên đoạn [−1; 1] ta dùng lệnh Max( , −1, 1), kết quả thể hiện ở hình vẽ sau
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: b) y= -3x^4+4x^2+căn 2 trên đoạn [−1; 1]; (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid27-1712560835.png)
Vậy giá trị lớn nhất của hàm số là 2,75.
Để tìm giá trị nhỏ nhất của hàm số trên đoạn [−1; 1] ta dùng lệnh Min( , −1, 1), kết quả thể hiện ở hình vẽ sau
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: b) y= -3x^4+4x^2+căn 2 trên đoạn [−1; 1]; (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid28-1712560851.png)
Vậy giá trị nhỏ nhất của hàm số là 1,41.
Câu 10:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
c) trên đoạn [1; 10];
 Xem đáp án
Xem đáp án
c) Để tìm giá trị lớn nhất của hàm số trên đoạn [1; 10] ta dùng lệnh Max( , 1, 10), kết quả thể hiện ở hình vẽ sau
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: c) y= x+ căn 5/x trên đoạn [1; 10]; (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid30-1712560939.png)
Vậy giá trị lớn nhất của hàm số là 10,22.
Để tìm giá trị nhỏ nhất của hàm số trên đoạn [1; 10] ta dùng lệnh Min( , 1, 10), kết quả thể hiện ở hình vẽ sau
![Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: c) y= x+ căn 5/x trên đoạn [1; 10]; (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid29-1712560931.png)
Vậy giá trị nhỏ nhất của hàm số là 2,99.
Câu 11:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
d) y = sin2x – x trên đoạn .
 Xem đáp án
Xem đáp án
d) Để tìm giá trị lớn nhất của hàm số y = sin2x – x trên đoạn ta dùng lệnh Max(sin2x – x, ), kết quả thể hiện ở hình vẽ sau
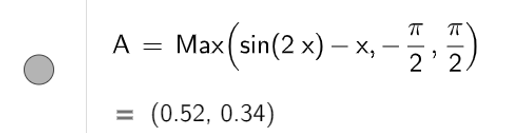
Vậy giá trị lớn nhất của hàm số là 0,34.
Để tìm giá trị nhỏ nhất của hàm số y = sin2x – x trên đoạn ta dùng lệnh Min( sin2x – x, ), kết quả thể hiện ở hình vẽ sau
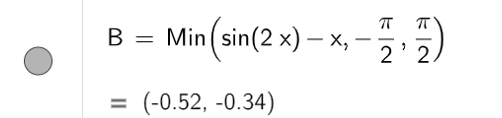
Vậy giá trị nhỏ nhất của hàm số là −0,34.
