Đề kiểm tra giữa học kì 2 Toán 7 Cánh Diều - Đề 01 có đáp án
-
217 lượt thi
-
20 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Thảo ghi chiều cao (cm) của các bạn học sinh tổ 1 lớp 7A được ghi lại trong bảng sau:
|
130 |
145 |
− 150 |
141 |
155 |
151 |
Số liệu không hợp lí là
Xem đáp án
Đáp án C
Câu 3:
Biểu đồ đoạn thẳng trong hình dưới đây biểu diễn điểm bài ôn luyện môn Khoa học của bạn Khanh từ tuần 1 đến tuần 5.
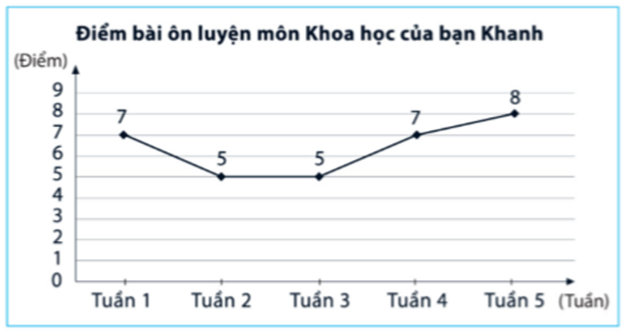
Hãy cho biết điểm 7 của bạn Khanh đạt vào tuần nào?
Xem đáp án
Đáp án B
Câu 4:
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn loại thực phẩm yêu thích trong 5 loại: Bánh rán, Nước ép, Bánh, Trà, Cà phê của học sinh khối 7 ở trường THCS Thanh Đa. Mỗi học sinh chỉ được chọn một loại thực phẩm khi được hỏi ý kiến như hình bên dưới.
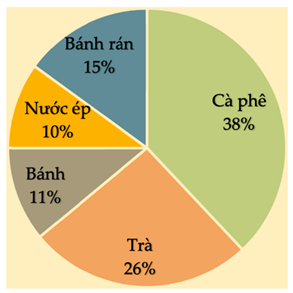
Hỏi tổng số học sinh chọn món Trà và Bánh rán chiếm bao nhiêu phần trăm?
Xem đáp án
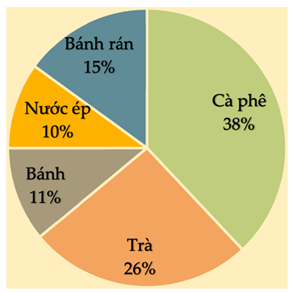
Tổng tỉ số phần trăm số học sinh chọn món Trà và Bánh rán là:
26% + 15% = 41%.
Câu 5:
Khi tung một đồng xu cân đối một lần và quan sát mặt xuất hiện của nó. Số kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là
Xem đáp án
Đáp án B
Câu 6:
Xác suất của biến cố trong trò chơi có 10 kết quả có thể xảy ra là . Số kết quả thuận lợi của biến cố đó là
Xem đáp án
Đáp án C
Gọi số kết quả thuận lợi của biến cố đó là k.
Khi đó xác suất của biến cố đó là \(\frac{k}{{10}}\).
Theo bài ta có: \(\frac{k}{{10}}\) = \(\frac{2}{5}\)
Suy ra k = 4.
Vậy số kết quả thuận lợi của biến cố là 4.
Câu 9:
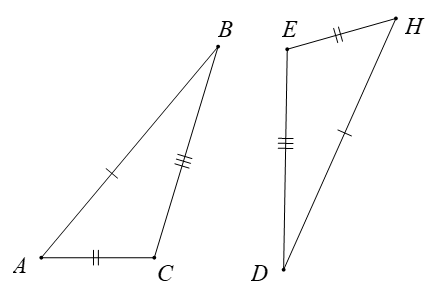
Cho ∆ABC = ∆MNP. Khẳng định nào dưới đây sai?
Xem đáp án
Đáp án C
Vì ∆ABC = ∆MNP nên:
\(\widehat A = \widehat M\); \(\widehat B = \widehat N\); \(\widehat C = \widehat P\) (các góc tương ứng bằng nhau)
AB = MN; BC = NP; AC = MP (các cạnh tương ứng bằng nhau)
Vậy AB = MP là khẳng định sai.
Câu 11:
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat C = \widehat M\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh?
Xem đáp án
Đáp án A
Vì tam giác ABC và tam giác NPM có BC = PM; \(\widehat C = \widehat M\).
Nên để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh cần thêm điều kiện AC = NM. (Do \(\widehat C\) là góc xen giữa hai cạnh BC và AC; \(\widehat M\) là góc xen giữa hai cạnh PM và NM).
Câu 12:
Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H và K. So sánh BH và CK.
Xem đáp án
Đáp án D
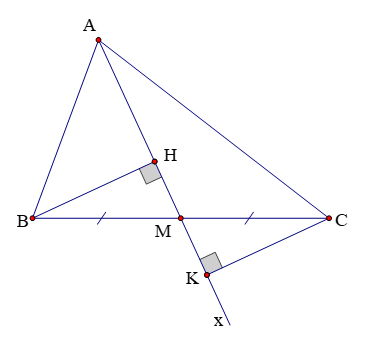
Xét hai tam giác vuông BHM và CKM có
BM = CM (vì M là trung điểm của BC)
\(\widehat {BMH} = \widehat {CMK}\) (hai góc đối đỉnh)
Suy ra ∆BHM và ∆CKM (cạnh huyền – góc nhọn).
Do đó BH = CK (hai cạnh tương ứng).
Câu 13:
Xét tính hợp lí của các dữ liệu trong mỗi bảng thống kê sau:
|
Lớp |
Sĩ số |
Số học sinh tham gia ngoại khóa |
|
7A1 |
39 |
42 |
|
7A2 |
42 |
10 |
|
7A3 |
45 |
15 |
|
7A4 |
43 |
26 |
|
Tổng |
169 |
60 |
Xem đáp án
Bảng thống kê này chưa hợp lí:
• Số học sinh lớp 7A1 tham gia ngoại khoá (42 học sinh) vượt quá sĩ số của lớp (39 học sinh);
• Tổng số học sinh tham gia ngoại khoá của các lớp là:
42 + 10 + 15 + 26 = 93 (học sinh).
Tổng số học sinh tham gia ngoại khoá của các lớp (93 học sinh) lớn hơn số học sinh ở phần tổng (60 học sinh) nên bảng thống kê này chưa hợp lí.
Câu 14:
Xét tính hợp lí của các dữ liệu trong mỗi bảng thống kê sau:
|
Kết quả kiểm tra thường xuyên môn Toán đợt 1 |
Tỉ lệ phần trăm |
|
Từ 8 điểm trở lên |
45% |
|
Từ 6,5 điểm đến 7,9 điểm |
110% |
|
Từ 5,0 điểm đến 6,4 điểm |
35% |
|
Từ 3,5 điểm đến 4,9 điểm |
10% |
|
Dưới 3,5 điểm |
200% |
Xem đáp án
Bảng thống kê này chưa hợp lí vì tỉ lệ phần trăm kết quả kiểm tra thường xuyên không thể vượt quá 100% (cột tỉ lệ phần trăm kiểm tra thường xuyên môn Toán đợt 1 dưới 3,5 điểm là 200% vượt quá 100%) và tổng các loại phải đúng bằng 100%.
Câu 15:
Một hộp có 48 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; …; 48. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương”.
Xem đáp án
Tập hợp các kết quả có thể xảy ra là: {1; 2; 3; … ; 47; 48}. Có 48 kết quả.
Trong các số trên, số chính phương là: 1; 4; 9; 16; 25; 36.
Do đó có 6 kết quả thuận lợi.
Khi đó, xác suất của biến cố đã cho là: \(\frac{6}{{48}} = \frac{1}{8}\).
Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương” bằng \(\frac{1}{8}\).
Câu 16:
Cho ∆ABC có AB < AC. Kẻ tia phân giác AD của \[\widehat {BAC}\] (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC.
Chứng minh ∆BDF = ∆EDC.
Xem đáp án
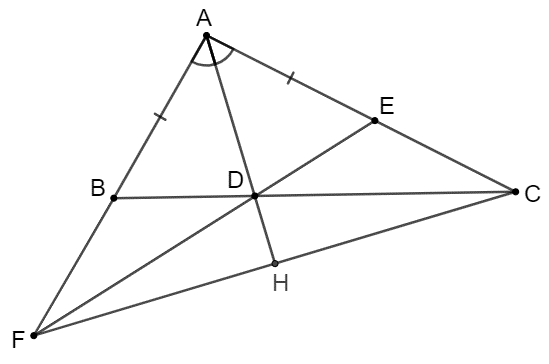
Xét ∆BDF và ∆EDC có:
AE = AB (giả thiết)
\(\widehat {BAD} = \widehat {EAD}\) (vì AD là tia phân giác của \[\widehat {BAC}\])
Cạnh AD chung
Do đó ∆BDF = ∆EDC (c.g.c).
Suy ra BD = ED (hai cạnh tương ứng); \(\widehat {ABD} = \widehat {AED}\) (hai cạnh tương ứng).
Mặt khác \(\widehat {ABD} + \widehat {DBF} = 180^\circ \); \[\widehat {AED} + \widehat {DEC} = 180^\circ \] nên \(\widehat {DBF} = \widehat {DEC}\).
Ta có AF = AC, AB = AE suy ra BF = EC.
Xét ∆BDF và ∆EDC có:
BF = EC (chứng minh trên)
\(\widehat {DBF} = \widehat {DEC}\) (chứng minh trên)
BD = ED (chứng minh trên)
Do đó ∆BDF = ∆EDC (c.g.c).
Câu 17:
Cho ∆ABC có AB < AC. Kẻ tia phân giác AD của \[\widehat {BAC}\] (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC.
Chứng minh ba điểm F, D, E thẳng hàng.
Xem đáp án
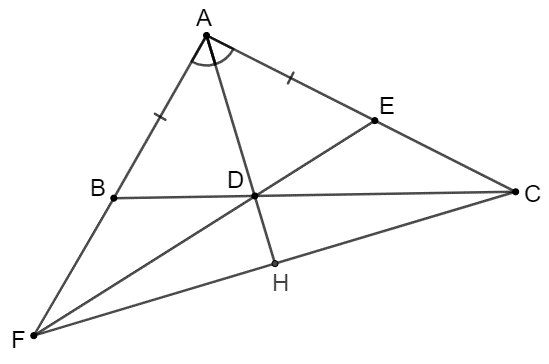
Từ câu a: ∆BDF = ∆EDC suy ra \(\widehat {BDF} = \widehat {EDC}\) (hai góc tương ứng).
Mà \(\widehat {BDF} + \widehat {FDC} = 180^\circ \) nên \(\widehat {EDC} + \widehat {FDC} = 180^\circ \).
Do đó ba điểm F, D, E thẳng hàng.
Câu 18:
Cho ∆ABC có AB < AC. Kẻ tia phân giác AD của \[\widehat {BAC}\] (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC.
Chứng minh AD ⊥ FC.
Xem đáp án
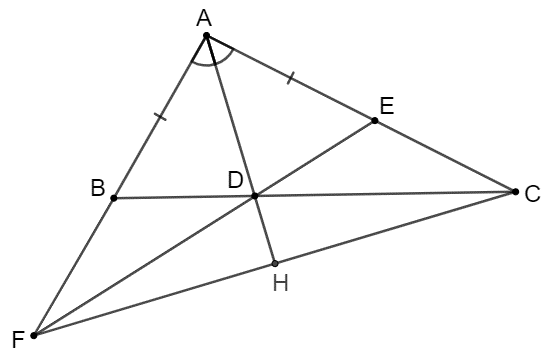
Gọi H là giao điểm của AD và CF.
Xét ∆AHF và ∆AHC có:
AF = AC (giả thiết)
\(\widehat {FAH} = \widehat {CAH}\) (vì AD là tia phân giác của \[\widehat {BAC}\])
Cạnh AH chung
Do đó ∆AHF = ∆AHC (c.g.c).
Suy ra \[\widehat {AHF} = \widehat {AHC}\] (hai cạnh tương ứng).
Mà \(\widehat {AHF} + \widehat {AHC} = 180^\circ \) suy ra \(\widehat {AHF} = \widehat {AHC} = 90^\circ \).
Vậy AH ⊥ FC hay AD ⊥ FC.
Câu 19:
Năm 2020, Việt Nam xuất khẩu (ước đạt) 6,5 triệu tấn gạo, thu được 3,07 tỉ đô la Mỹ. Biểu đồ hình quạt tròn ở bên dưới biểu diễn khối lượng xuất khẩu của mỗi loại gạo trong tổng số gạo xuất khẩu (tính theo tỉ số phần trăm).
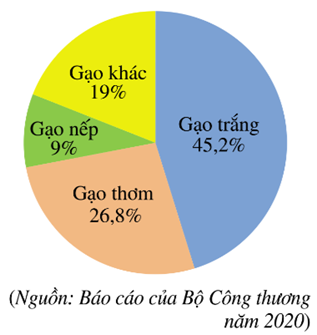
Dựa vào thông tin thu thập từ biểu đồ trên để trả lời các câu hỏi sau:
Tính số lượng gạo trắng và số lượng gạo nếp được xuất khẩu năm 2020?
Xem đáp án
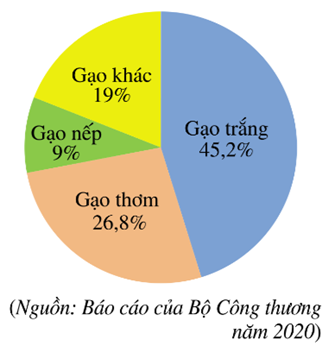
Số lượng gạo trắng được xuất khẩu năm 2020 là:
6,5 . 45,2% = 2,938 (triệu tấn).
Số lượng gạo nếp được xuất khẩu năm 2020 là:
6,5 . 9% = 0,585 (triệu tấn).
Vậy số lượng gạo trắng và số lượng gạo nếp được xuất khẩu năm 2020 lần lượt là 2,938 triệu tấn và 0,585 triệu tấn.
Câu 20:
Năm 2020, Việt Nam xuất khẩu (ước đạt) 6,5 triệu tấn gạo, thu được 3,07 tỉ đô la Mỹ. Biểu đồ hình quạt tròn ở bên dưới biểu diễn khối lượng xuất khẩu của mỗi loại gạo trong tổng số gạo xuất khẩu (tính theo tỉ số phần trăm).
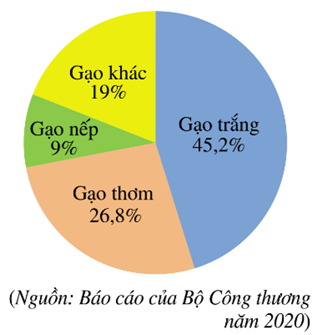
Dựa vào thông tin thu thập từ biểu đồ trên để trả lời các câu hỏi sau:
Số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm là bao nhiêu?
Xem đáp án
Số lượng gạo thơm được xuất khẩu là:
6,5 . 26,8% = 1,742 (triệu tấn).
Tỉ số phần trăm số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm là:
2,938 – 1,742 = 1,196 (triệu tấn).
Vậy số lượng gạo trắng xuất khẩu nhiều hơn số lượng gạo thơm 1,196 triệu tấn.