Đề kiểm tra giữa học kì 2 Toán 7 Cánh Diều - Đề 02 có đáp án
-
299 lượt thi
-
20 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 3:
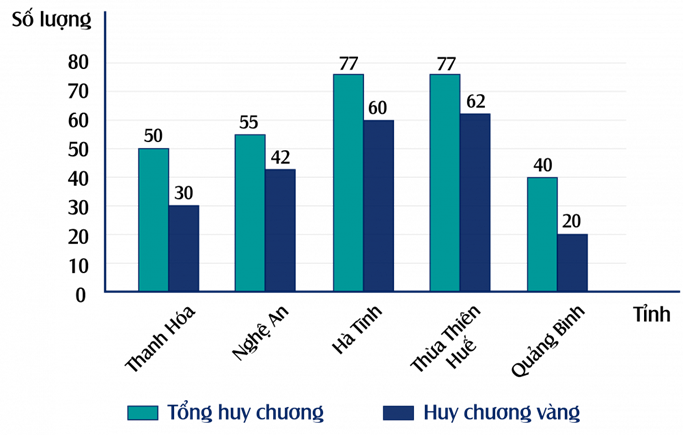
Cho biểu đồ đoạn thẳng như hình vẽ.
Biểu đồ trên có 6 điểm và mỗi điểm được xác định bởi
 Xem đáp án
Xem đáp án
Đáp án B
Câu 4:
Cho biểu đồ sau.
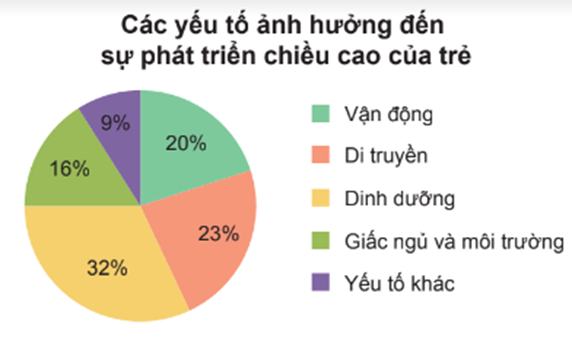
Trong biểu đồ trên, yếu tố ảnh hưởng đến 23% sự phát triển chiều cao của trẻ là
 Xem đáp án
Xem đáp án
Đáp án D
23% được ghi ở hình quạt tròn màu hồng. Mà hình quạt tròn đó biểu diễn yếu tố di truyền.
Do đó, yếu tố ảnh hưởng đến 23% sự phát triển chiều cao của trẻ là di truyền.
Câu 6:
Vòng tứ kết cuộc thi bơi lội có sáu trường với 8 học sinh đại diện tham gia:
THCS Nguyễn Huệ: Kiệt;
THCS Nguyễn Khuyến: Long;
THCS Chu Văn An: Nguyên và Đăng;
THCS Nguyễn Bỉnh Khiêm: Minh;
THCS Lưu Văn Liệt: Thành;
THCS Nguyễn Du: Kha và Bình.
Xét biến cố “Người chiến thắng là học sinh đến từ trường THCS Nguyễn Huệ hoặc THCS Nguyễn Du”. Tính xác suất của biến cố trên.
 Xem đáp án
Xem đáp án
Đáp án B
Có 8 học sinh tham gia nên có 8 kết quả có thể xảy ra.
Trường THCS Nguyễn Huệ có 1 học sinh và THCS Nguyễn Du có 2 học sinh nên có 3 kết quả thuận lợi cho biến cố “Người chiến thắng là học sinh đến từ trường THCS Nguyễn Huệ hoặc THCS Nguyễn Du”.
Do đó xác suất của biến cố trên là: 38.
Câu 8:
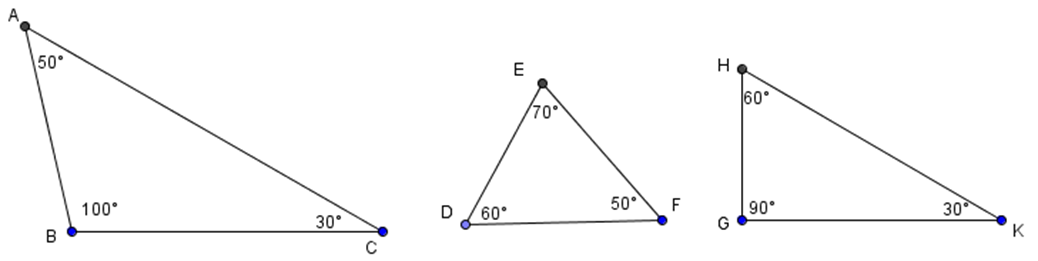
Cho tam giác MNP có ˆM=80∘ và ˆN=50∘. So sánh độ dài NP và MP là
 Xem đáp án
Xem đáp án
Đáp án A
Trong tam giác MNP có: ˆM=80∘ và ˆN=50∘ (giả thiết)
Nên ˆM>ˆN
Do đó NP > MP.
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có ∆ABC = ∆MNP (giả thiết)
Suy ra: AB = MN; BC = NP; AC = MP (các cạnh tương ứng bằng nhau)
ˆA=ˆM; ˆB=ˆN; ˆC=ˆP (các góc tương ứng bằng nhau)
Vậy BC = MP là khẳng định sai.
Câu 10:
Cho tam giác ABC và tam giác MNP có AB = MP, AC = NM, BC = NP. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 12:
Cho hình vẽ sau, trong đó AB // CD, AB = CD.
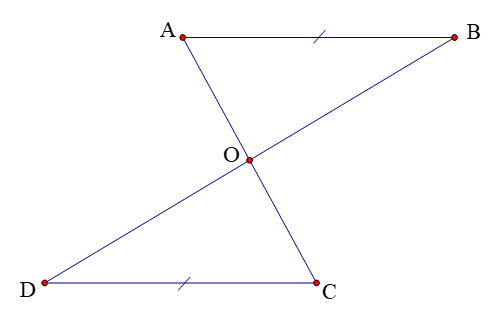
Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án C
Xét ∆AOB và ∆COD có:
^OAB=^OCD (hai góc so le trong do AB // CD)
AB = CD (gt)
^OBA=^ODC (hai góc so le trong do AB // CD)
Do đó, ∆AOB = ∆COD (g.c.g)
Suy ra OA = OC (hai cạnh tương ứng)
Do đó O là trung điểm của AC.
Câu 13:
Kết quả tìm hiểu về kết quả xếp loại học lực của các bạn học sinh khối 7 được cho bởi bảng thống kê sau:
|
Xếp loại học lực của học sinh khối 7 |
||||
|
Loại |
Giỏi |
Khá |
Trung bình |
Yếu |
|
Số học sinh |
120 |
285 |
150 |
25 |
Hãy phân loại các dữ liệu trong bảng thống kê trên dựa trên tiêu chí định tính và định lượng.
 Xem đáp án
Xem đáp án
Dữ liệu định tính là: kết quả xếp loại học lực.
Dữ liệu định lượng là: số bạn học sinh tham gia xếp loại.
Câu 14:
Kết quả tìm hiểu về kết quả xếp loại học lực của các bạn học sinh khối 7 được cho bởi bảng thống kê sau:
|
Xếp loại học lực của học sinh khối 7 |
||||
|
Loại |
Giỏi |
Khá |
Trung bình |
Yếu |
|
Số học sinh |
120 |
285 |
150 |
25 |
Dữ liệu trên có đại diện cho kết quả học tập của các bạn học sinh khối 7 hay không? Vì sao?
 Xem đáp án
Xem đáp án
Dữ liệu trên đủ điều kiện đại diện được cho kết quả xếp loại học lực của học sinh khối 7 vì đối tượng khảo sát đã bao gồm tất cả các bạn học sinh là nam và nữ trong khối 7.
Câu 15:
Một nhóm du khách gồm 11 người đến từ các quốc gia: Anh; Pháp; Mỹ; Thái Lan; Bỉ; Ấn Độ; Hà Lan; Cu Ba; Nam Phi; Nhật Bản; Brasil. Chọn ngẫu nhiên một người trong nhóm du khách trên. Tính xác suất của biến cố “Du khách được chọn đến từ châu Âu”.
 Xem đáp án
Xem đáp án
Có 11 du khách ứng với 11 quốc gia nên có 11 kết quả có thể xảy ra.
Các kết quả thuận lợi của biến cố “Du khách được chọn đến từ châu Âu” là: Anh; Pháp; Bỉ; Hà Lan. Có 4 kết quả thuận lợi.
Vì vậy, xác suất của biến cố trên là: 411.
Câu 16:
Cho góc bẹt xOy có tia phân giác Ot. Trên tia Ot lấy hai điểm A, B (A nằm giữa O và B). Lấy điểm C ∈ Ox sao cho OC = OB, lấy điểm D ∈ Oy sao cho OD = OA.
Chứng minh AC = BD và AC ⊥ BD.
 Xem đáp án
Xem đáp án
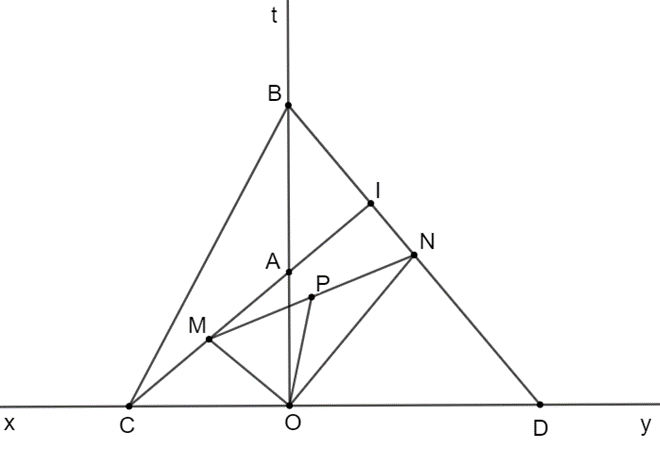
Vì góc xOy bẹt có Ot là tia phân giác nên Ot ⊥ xy.
Suy ra ^COA=^DOB=90∘.
Xét ∆AOC và ∆DOB có:
OC = OB (giả thiết)
^COA=^DOB=90∘ (chứng minh trên)
OD = OA (giả thiết)
Do đó ∆AOC = ∆DOB (c.g.c)
Suy ra DB = AC (hai cạnh tương ứng)
Gọi E là giao điểm của AC và BD.
Ta có ^EAB+^EBA=^OCA+^OAC=90∘.
Suy ra ∆AEB vuông tại E nên AC ⊥ BD.
Câu 17:
Cho góc bẹt xOy có tia phân giác Ot. Trên tia Ot lấy hai điểm A, B (A nằm giữa O và B). Lấy điểm C ∈ Ox sao cho OC = OB, lấy điểm D ∈ Oy sao cho OD = OA.
 Xem đáp án
Xem đáp án
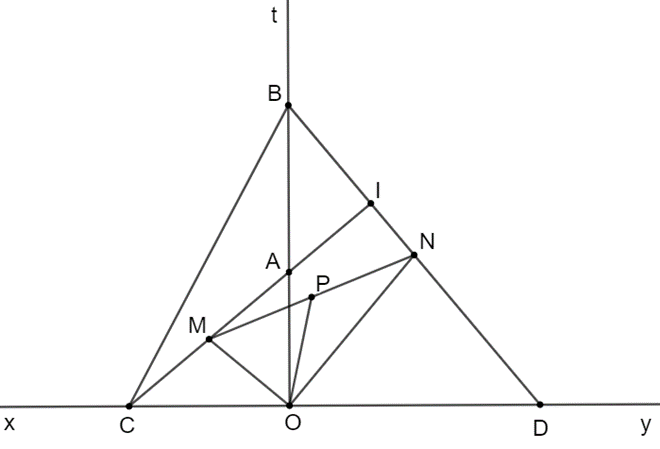
Vì AC = BD (chứng minh trên) mà M, N lần lượt là trung điểm của AC, BD
Nên BN = DN = AM = CM.
Xét ∆ONB và ∆OMC có:
BN = CM (chứng minh trên)
^DBO=^ACO (vì ∆AOC = ∆DOB)
OC = OB (giả thiết)
Do đó ∆ONB = ∆OMC (c.g.c)
Suy ra OM = ON (hai cạnh tương ứng).
Câu 18:
Cho góc bẹt xOy có tia phân giác Ot. Trên tia Ot lấy hai điểm A, B (A nằm giữa O và B). Lấy điểm C ∈ Ox sao cho OC = OB, lấy điểm D ∈ Oy sao cho OD = OA.
Tính các góc của tam giác MON.
 Xem đáp án
Xem đáp án
Từ câu b: ∆ONB = ∆OMC suy ra ^NOB=^MOC (hai góc tương ứng)
Ta có ^NOB+^BOM=^BOM+^MOC=90∘.
Gọi P là trung điểm của MN.
Xét ∆NOP và ∆MOP có:
OM = ON (chứng minh trên)
MP = NP (vì P là trung điểm của MN)
Cạnh OP chung
Do đó ∆NOP = ∆MOP (c.c.c)
Suy ra ^OMP=^ONP (hai cạnh tương ứng)
Do đó ^OMN=^ONM=180∘−^MON2=90∘2=45∘.
Vậy các góc của tam giác MON là ^MON=90∘;^OMN=45∘;^ONM=45∘.
Câu 19:
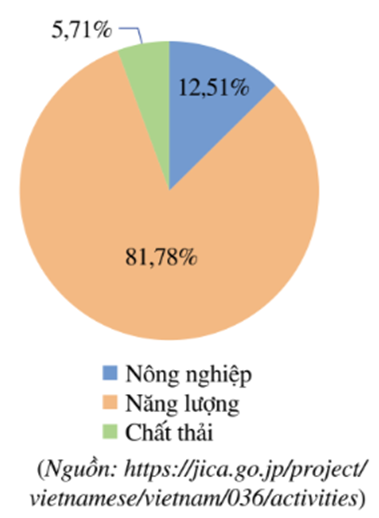
Dựa vào biểu đồ trên, hãy trả lời các câu hỏi sau:
Tính lượng khí nhà kính được tạo ra ở lĩnh vực Năng lượng và Chất thải của Việt Nam vào năm 2020. Biết rằng tổng lượng phát thải khí nhà kính trong ba lĩnh vực trên của Việt Nam vào năm 2020 là 466 triệu tấn khí cacbonic tương đương (tức là những khí nhà kính khác đều được quy đổi về khí cacbonic khi tính khối lượng).
 Xem đáp án
Xem đáp án
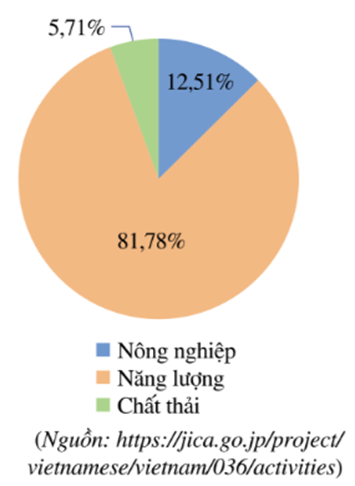
Lượng khí nhà kính được tạo ra ở lĩnh vực Năng lượng của Việt Nam vào năm 2020 là:
466 . 81,78% = 381,0948 (triệu tấn khí carbonic tương đương)
Lượng khí nhà kính được tạo ra ở lĩnh vực chất thải của Việt Nam vào năm 2020 là:
466 . 5,71% = 26,6086 (triệu tấn khí carbonic tương đương).
Vậy lượng khí nhà kính được tạo ra của Việt Nam vào năm 2020 ở lĩnh vực Năng lượng là 381,0948 triệu tấn khí carbonic tương đương và Chất thải là 26,6086 triệu tấn khí carbonic tương đương.
Câu 20:
Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn lượng phát thải khí nhà kính trong ba lĩnh vực: Nông nghiệp, Năng lượng, Chất thải vào năm 2020 của Việt Nam (tính theo tỉ số phần trăm).
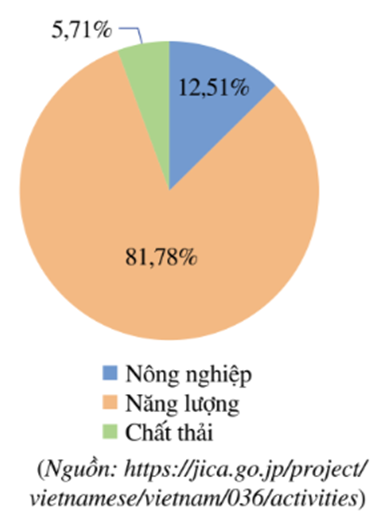
Dựa vào biểu đồ trên, hãy trả lời các câu hỏi sau:
Nêu hai biện pháp mà chính phủ Việt Nam đã đưa ra nhằm giảm lượng khí thải và giảm bớt tác động của khí nhà kính.
 Xem đáp án
Xem đáp án
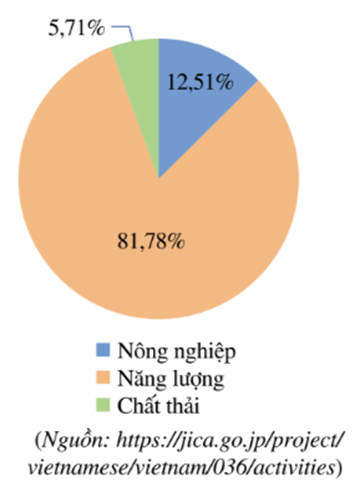
Nêu đúng hai trong những biện pháp sau:
- Trồng nhiều cây xanh, không phá rừng bừa bãi.
- Sử dụng hiệu quả và tiết kiệm năng lượng; sử dụng và phát triển những nguồn năng lượng sạch.
- Khuyến khích người dân sử dụng phương tiện công cộng.
- Tái sử dụng và tái chế những vật dụng có khả năng tái sử dụng và tái chế.
- Tuyên truyền, nâng cao ý thức và giáo dục người dân về hậu quả của khí thải, hiệu ứng nhà kính.