Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 2
-
2012 lượt thi
-
38 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 4:
Cho hàm số y = f(x) có đồ thị như hình dưới đây.
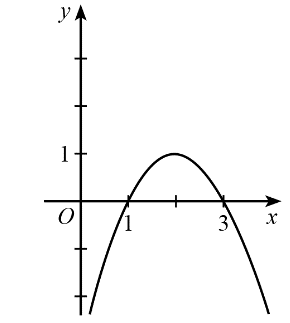
Trong các phát biểu sau, phát biểu nào sai?
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: x2 – 8x + 7 ≥ 0 ⇔ \(\left[ \begin{array}{l}x \le 1\\x \ge 7\end{array} \right.\).
Suy ra tập nghiệm của bất phương trình là S = (– ∞; 1] ∪ [7; + ∞].
Do đó, [6; + ∞) ⊄ S.
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình – x2 + 2(m – 1)x + m – 3 = 0 có hai nghiệm phân biệt khi và chỉ khi ∆' > 0
⇔ (m – 1)2 – (– 1) . (m – 3) > 0 ⇔ m2 – m – 2 > 0 \( \Leftrightarrow \left[ \begin{array}{l}m < - 1\\m > 2\end{array} \right.\).
Vậy m ∈ (– ∞; – 1) ∪ (2; + ∞).
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bình phương hai vế của phương trình \[\sqrt { - {x^2} + 4x} = 2x - 2\] ta được
– x2 + 4x = 4x2 – 8x + 4.
Sau khi thu gọn ta được 5x2 – 12x + 4 = 0. Từ đó tìm được x = 2 hoặc \(x = \frac{2}{5}\).
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cách 1. Thay lần lượt các giá trị ở từng đáp án vào cho đến khi tìm được giá trị thỏa mãn.
Cách 2. Giải phương trình
Bình phương hai vế của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \) ta được
3x2 – 6x + 1 = x2 – 3.
Rút gọn ta được x2 – 3x + 2 = 0. Từ đó ta tìm được x = 1 hoặc x = 2.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
\(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \)\( \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 4x - 3 \ge 0\\ - {x^2} + 4x - 3 = 2m + 3x - {x^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 3\\x = 2m + 3\end{array} \right.\)
Để phương trình (1) có nghiệm thì 1 ≤ 2m + 3 ≤ 3 ⇔ – 1 ≤ m ≤ 0 ⇒ m ∈ [– 1; 0].
Suy ra a = – 1, b = 0, do đó a2 + b2 = 1.
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \overrightarrow a = k\overrightarrow b \)\( \Rightarrow \left\{ \begin{array}{l}4 = k\left( {2m + 6} \right)\\ - m = k\end{array} \right. \Rightarrow \left[ \begin{array}{l}m = - 1\\m = - 2\end{array} \right.\).
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\overrightarrow {AB} = \left( { - 2;\,\, - 1} \right),\,\,\overrightarrow {AC} = \left( {4;\,\, - 3} \right)\).
Do đó, \(\overrightarrow {AB} \cdot \overrightarrow {AC} = \left( { - 2} \right) \cdot 4 + \left( { - 1} \right) \cdot \left( { - 3} \right) = - 8 + 3 = - 5\).
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Cách 1. Thay tọa độ các điểm A, B lần lượt vào các phương trình trong các đáp án thì thấy đáp án B không thỏa mãn.
Cách 2. Nhận thấy rằng các phương trình ở các đáp án A, C, D thì vectơ chỉ phương của các đường thẳng đó cùng phương, riêng chủ có đáp án B thì không. Do đó chọn đáp án B.
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {6;\,\, - 5} \right)\);
Đường thẳng b có một vectơ chỉ phương là \(\overrightarrow {{u_2}} = \left( { - 6;\,\,5} \right)\) nên nó có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {5;\,6} \right)\).
Ta thấy: \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 6 \cdot 5 + \left( { - 5} \right) \cdot 6 = 0\).
Suy ra góc giữa hai đường thẳng bằng 90°.
Câu 28:
 Xem đáp án
Xem đáp án
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính bằng nửa độ dài đoạn AB.
Ta có \(\overrightarrow {AB} = \left( {4;\,\, - 4} \right)\), suy ra \(AB = \sqrt {{4^2} + {{\left( { - 4} \right)}^2}} = 4\sqrt 2 \).
Suy ra bán kính đường tròn là \(R = \frac{{AB}}{2} = 2\sqrt 2 \).
Tọa độ tâm là \(\left\{ \begin{array}{l}{x_I} = \frac{{1 + 5}}{2} = 3\\{y_I} = \frac{{3 + \left( { - 1} \right)}}{2} = 1\end{array} \right.\). Suy ra I(3; 1).
Phương trình đường tròn cần lập là: (x – 3)2 + (y – 1)2 = 8.
Câu 30:
Câu 31:
Trong mặt phẳng tọa độ Oxy, elip nào dưới đây có phương trình chính tắc dạng
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,\left( {a > b > 0} \right)\)?
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 32:
 Xem đáp án
Xem đáp án
Câu 33:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: 16x2 + 25y2 = 400 \( \Leftrightarrow \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
Do đó, elip (E) có a = 5, b = 4, nên c = 3.
Vậy (E) có trục nhỏ bằng 2b = 8, có trục lớn bằng 2a = 10, có tiêu cự bằng 2c = 6 và có các tiêu điểm F1(– 3; 0) và F2(3; 0). Do đó, đáp án B sai.
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: a2 = 5 và b2 = 4 nên c2 = a2 + b2 = 9, suy ra c = 3.
Vậy tiêu cự của hypebol là 2c = 6.
Câu 36:
Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
 Xem đáp án
Xem đáp án
Đáp án:
a) Gọi đường thẳng cần lập là d.
Vectơ pháp tuyến của đường thẳng 3x + 5y – 2 = 0 cũng là một vectơ pháp tuyến của đường thẳng d nên phương trình đường thẳng d có dạng 3x + 5y + c = 0 (c ≠ – 2).
Vì d đi qua điểm M(– 1; – 4) nên 3 . (– 1) + 5 . (– 4) + c = 0. Suy ra c = 23 (t/m).
Vậy phương trình tổng quát của đường thẳng d là 3x + 5y + 23 = 0.
b) Gọi đường thẳng cần lập là a.
Đường thẳng a vuông góc với đường thẳng 2x + 3y + 7 nên lấy vectơ pháp tuyến \(\overrightarrow n = \left( {2;\,\,3} \right)\) của đường thẳng 2x + 3y + 7 là vectơ chỉ phương của đường thẳng a. Khi đó, một vectơ pháp tuyến của đường thẳng a là \(\overrightarrow {{n_a}} = \left( {3;\,\, - 2} \right)\).
Đường thẳng a đi qua điểm N(1; 1) và có vectơ pháp tuyến là \(\overrightarrow {{n_a}} = \left( {3;\,\, - 2} \right)\) nên có phương trình là 3(x – 1) – 2(y – 1) = 0 hay 3x – 2y – 1 = 0.
Câu 37:
 Xem đáp án
Xem đáp án
Đáp án:
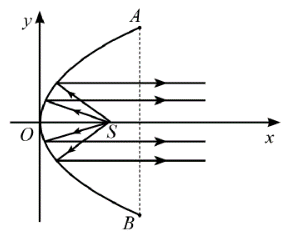
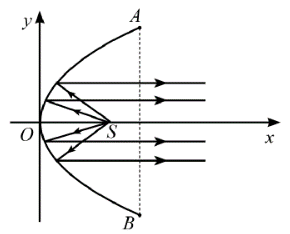
Parabol có phương trình chính tắc là: y2 = 2px (p > 0).
Vì AB = 40 cm và h = 30 cm nên A(30; 20).
Do A(30; 20) thuộc parabol nên ta có: 202 = 2p . 30 \( \Rightarrow p = \frac{{20}}{3}\).
Vậy parabol có phương trình chính tắc là: y2 = \(\frac{{40}}{3}x\).
Câu 38:
 Xem đáp án
Xem đáp án
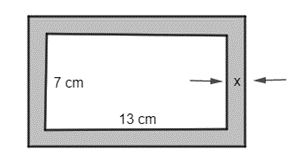
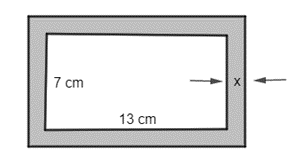
Diện tích hình chữ nhật bên trong khung ảnh (không bao gồm viền) là 7 . 13 = 91 (cm2).
Vì độ rộng viền xung quanh là x cm nên x > 0 và kích thước của khung ảnh là (7 + 2x) cm × (13 + 2x) cm.
Diện tích viền khung ảnh là: (7 + 2x)(13 + 2x) – 91 = 4x2 + 40x (cm2).
Theo bài ra ta có: 4x2 + 40x ≤ 44.
Giải bất phương trình trên ta được x ∈ [– 11; 1]. Do x > 0 nên x ∈ (0; 1].
Vậy độ rộng viền khung ảnh lớn nhất là 1 cm.
