Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 1
-
1942 lượt thi
-
38 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án: D
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình x2 – (m + 1)x + 1 = 0 vô nghiệm khi và chỉ khi ∆ < 0 ⇔ (m + 1)2 – 4 < 0
⇔ m2 + 2m – 3 < 0 ⇔ – 3 < m < 1.
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bình phương hai vế của phương trình \(\sqrt {4 - 3{x^2}} = 2x - 1\) ta được
4 – 3x2 = 4x2 – 4x + 1.
Sau khi thu gọn ta được 7x2 – 4x – 3 = 0. Từ đó tìm được x = 1 hoặc \(x = - \frac{3}{7}\).
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 1 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 1.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cách 1. Thay lần lượt các giá trị ở từng đáp án vào cho đến khi tìm được giá trị thỏa mãn.
Cách 2. Giải phương trình
Bình phương hai vế của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \) ta được
3x2 – 6x + 1 = x2 – 3.
Rút gọn ta được x2 – 3x + 2 = 0. Từ đó ta tìm được x = 1 hoặc x = 2.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 14:
 Xem đáp án
Xem đáp án
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
\(\overrightarrow c = \overrightarrow a + 3\overrightarrow b \) = (2; – 1) + 3 . (3; 4) = (2; – 1) + (9; 12) = (2 + 9; – 1 + 12) = (11; 11).
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\cos \left( {\overrightarrow x ,\,\overrightarrow y } \right) = \frac{{\overrightarrow x \cdot \overrightarrow y }}{{\left| {\overrightarrow x } \right| \cdot \left| {\overrightarrow y } \right|}} = \frac{{1.\left( { - 2} \right) + \left( { - 2} \right).\left( { - 6} \right)}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 6} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\).
Do đó, \(\left( {\overrightarrow x ,\,\overrightarrow y } \right) = 45^\circ \).
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 22:
 Xem đáp án
Xem đáp án
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng d: \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = x - 5\\y = - 9 - 2t\end{array} \right.\)⇒ y = – 9 – 2 . (x – 5) ⇔ 2x + y – 1 = 0.
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Khoảng cách từ điểm A(1; 1) đến d: 5x – 12y – 6 = 0 là
\(d\left( {A,\,\,d} \right) = \frac{{\left| {5 \cdot 1 - 12 \cdot 1 - 6} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = 1\).
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ;\,\, - 1} \right)\);
Đường thẳng b có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1;\, - \sqrt 3 } \right)\).
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
\(\cos \left( {a,\,\,b} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 \cdot 1 + \left( { - 1} \right) \cdot \left( { - \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} \cdot \sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}\).
Suy ra góc giữa hai đường thẳng bằng 30°.
Câu 28:
 Xem đáp án
Xem đáp án
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 nên bán kính đường tròn chính là khoảng cách từ tâm I đến đường thẳng ∆.
Ta có: R = d(I, ∆) = \(\frac{{\left| {3 \cdot 3 + 4 \cdot 4 - 10} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3\).
Vậy phương trình đường tròn cần tìm là: (x – 3)2 + (y – 4)2 = 9.
Câu 30:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn (C) có tâm là I(2; – 2). Tiếp tuyến của (C) tại M(1; 0) có vectơ pháp tuyến \(\overrightarrow {MI} = \left( {1;\, - 2} \right)\), nên có phương trình
1(x – 1) – 2(y – 0) = 0 hay x – 2y – 1 = 0.
Câu 31:
 Xem đáp án
Xem đáp án
Đáp án: D
Câu 32:
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 34:
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\,\,\left( {a,\,b > 0} \right)\).
Từ giả thiết ta có: \(\left\{ \begin{array}{l}\frac{c}{a} = 2\\2c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\c = 2\end{array} \right. \Rightarrow b = \sqrt {{2^2} - {1^2}} = \sqrt 3 \).
Vậy (H) có phương trình là: \(\frac{{{x^2}}}{{{1^2}}} - \frac{{{y^2}}}{{{{\left( {\sqrt 3 } \right)}^2}}} = 1\,\,\,hay\,\,\,{x^2} - \frac{{{y^2}}}{3} = 1\).
Câu 36:
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:
20 khách đầu tiên có giá là 300 000 đồng/người. Nếu có nhiều hơn 20 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 10 000 đồng/người cho toàn bộ hành khách.
a) Gọi x là số lượng khách từ người thứ 21 trở lên của nhóm. Biểu thị doanh thu của công ty theo x.
b) Số người từ người thứ 21 trở lên của nhóm khách du lịch trong khoảng bao nhiêu thì công ty có lãi? Biết rằng chi phí của chuyến đi là 4 000 000 đồng.
 Xem đáp án
Xem đáp án
Đáp án:
a) Nếu có thêm x người khách thì số khách là 20 + x (người). Vì cứ có thêm 1 người, giá vé sẽ giảm 10 000 đồng/người cho toàn bộ hành khách, khi đó giá vé của mỗi người là:
300 000 – x . 10 000 = 300 000 – 10 000x (đồng).
Theo đó, doanh thu của công ty là:
(20 + x)(300 000 – 10 000x) = – 10 000x2 + 100 000x + 6 000 000.
b) Lợi nhuận của công ty là:
(– 10 000x2 + 100 000x + 6 000 000) – 4 000 000 = – 10 000x2 + 100 000x + 2 000 000.
Xét tam thức bậc hai f(x) = – 10 000x2 + 100 000x + 2 000 000, ta thấy f(x) có hai nghiệm là x1 = – 10, x2 = 20.
Áp dụng định lí về dấu của tam thức bậc hai, ta có bảng xét dấu sau:

Công ty lãi khi f(x) > 0, tức là – 10 < x < 20. Vì x ≥ 0 nên ta có 0 ≤ x < 20.
Vậy số khách từ người thứ 21 trở lên có ít hơn 20 người thì công ty có lãi.
Câu 37:
 Xem đáp án
Xem đáp án
Đáp án:
Gọi tọa độ các điểm A, B và M là A(xA; yA); B(xB; yB) và M(xM; yM).
Vì A thuộc d1 nên 2xA – yA – 2 = 0. Suy ra yA = 2xA – 2.
Vì B thuộc d2 nên xB + yB + 3 = 0. Suy ra yB = – xB – 3.
Do M là trung điểm của đoạn AB nên
\(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 6\\\left( {2{x_A} - 2} \right) + \left( { - {x_B} - 3} \right) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = \frac{{11}}{3}\\{y_A} = \frac{{16}}{3}\end{array} \right.\).
Suy ra \(A\left( {\frac{{11}}{3};\,\,\frac{{16}}{3}} \right)\).
Đường thẳng ∆ đi qua điểm A và điểm M.
Ta có: \(\overrightarrow {AM} = \left( { - \frac{2}{3};\,\, - \frac{{16}}{3}} \right)\)\( \Rightarrow \overrightarrow {{u_{AM}}} = \left( {1;\,\,8} \right) \Rightarrow \overrightarrow {{n_{AM}}} = \left( {8;\,\, - 1} \right)\).
Đường thẳng ∆ đi qua M(3; 0) và có một vectơ pháp tuyến là \(\overrightarrow {{n_{AM}}} \) nên có phương trình là
8(x – 3) – (y – 0) = 0 hay 8x – y – 24 = 0.
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án:
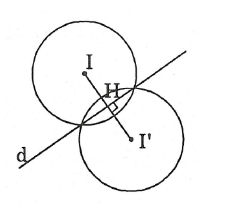
(C) có tâm I(1; 2), bán kính R = 2.
Phương trình đường thẳng ∆ đi qua I, vuông góc với d có dạng x + y + m = 0.
I (1; 2) ∈ ∆, suy ra 1 + 2 + m = 0 ⇒ m = – 3.
Do đó, phương trình đường thẳng ∆: x + y – 3 = 0.
Gọi H là giao điểm của ∆ và d. Tọa độ của H là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}{\rm{x}} + {\rm{y}} - 3 = 0\\{\rm{x}} - {\rm{y}} - 1 = 0\end{array} \right.\]
Từ đó tìm được H(2; 1).
Chứng minh được H là trung điểm của II' với I' là tâm của (C'). Suy ra I'(3; 0)
Vì (C), (C') đối xứng nhau qua d nên R = R'.
Vậy phương trình (C'): (x – 3)2 + y2 = 4.
Tọa độ giao điểm của (C), (C') là nghiệm của hệ phương trình:
\[\left\{ \begin{array}{l}{\left( {{\rm{x}} - 1} \right)^2} + {\left( {{\rm{y}} - 2} \right)^2} = 4\\{\left( {{\rm{x}} - 3} \right)^2} + {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {{\rm{x}} - 1} \right)^2} + {\left( {{\rm{y}} - 2} \right)^2} = 4\\{\rm{x}} - {\rm{y}} - 1 = 0\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}{{\rm{x}}_{\rm{1}}} = 1 \Rightarrow {{\rm{y}}_{\rm{1}}} = 0\\{{\rm{x}}_{\rm{2}}} = 3 \Rightarrow {{\rm{y}}_2} = 2\end{array} \right. \Rightarrow {\rm{A}}\left( {1;0} \right),\,\,{\rm{B}}\left( {3;2} \right)\] là giao điểm của (C), (C').
