Đề kiểm tra cuối học kì 2 Toán lớp 7 CTST - Đề 02 có đáp án
-
288 lượt thi
-
20 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Chọn câu đúng. Với điều kiện các tỉ số đều có nghĩa thì từ xy=uv ta có
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo tính chất của dãy tỉ số bằng nhau ta có: xy=uv=x+uy+v=x−uy−v nên A đúng.
Câu 2:
Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Áp dụng tính chất tỉ lệ thuận và tính chất dãy tỉ số bằng nhau
Vì x và y là hai đại lượng tỉ lệ thuận nên x1x2=y1y2
Suy ra x1−4=y13=y1−x13−(−4)=77=1
Nên x1 = 1.(–4) = –4; y1 = 1.3 = 3.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Các biến trong biểu thức đại số ax + by là x; y.
Câu 4:
Giá trị của biểu thức x + 2x2y – y2 tại x = –1 và y = –1 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Thay x = –1 và y = –1 vào biểu thức đã cho ta được: –1 + 2.(–1)2.(–1) – (–1)2 = –4.
Câu 5:
Chọn khẳng định đúng.
Xét tam giác ABC có:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo bất đẳng thức trong tam giác ta có AB + BC > AC.
Câu 6:
Cho tam giác ABC có AH ⊥ BC (H ∈ BC) thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
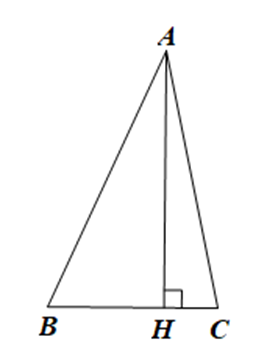
AB, AH lần lượt là đường xiên, đường vuông góc kẻ từ A đến BC. Do đó AB > AH.
Câu 7:
Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
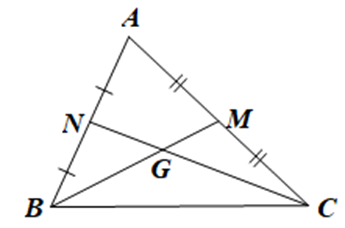
Cho DABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của DABC.
Khi đó CG=23CN; GN=12GC; GM=13BM; GB=2GM. Do đó C sai.
Câu 8:
Khẳng định nào sau đây là không đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Biến cố ngẫu nhiên A có xác suất như sau: 0 < P(A) < 1.
Câu 10:
Tìm x, biết:
(2x + 3)(x + 2) = (x – 4)(2x + 1)
 Xem đáp án
Xem đáp án
(2x + 3)(x + 2) = (x – 4)(2x + 1)
2x2 + 4x + 3x + 6 = 2x2 + x – 8x – 4
14x = –10
x=−57
Vậy x=−57.
Câu 11:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.
 Xem đáp án
Xem đáp án
P(x) = 6x5 + 15 – 7x – 4x2 – x5
= 5x5 – 4x2 – 7x + 15.
Q(x) = –5x5 – 2x + 4x2 + 5x – 7
= –5x5 + 4x2 + 3x – 7.
Câu 12:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
 Xem đáp án
Xem đáp án
K(x) = P(x) – Q(x)
K(x) = (5x5 – 4x2 – 7x + 15) – (–5x5 + 4x2 + 3x – 7)
= 5x5 – 4x2 – 7x + 15 + 5x5 – 4x2 – 3x + 7
= 10x5 – 8x2 – 10x + 22.
Đa thức K(x) có bậc là 5, hệ số cao nhất là 10.
Câu 13:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
 Xem đáp án
Xem đáp án
M(x) = P(x) + Q(x).
M(x) = (5x5 – 4x2 – 7x + 15) + (–5x5 + 4x2 + 3x – 7)
= 5x5 – 4x2 – 7x + 15 – 5x5 + 4x2 + 3x – 7
= –4x + 8.
Ta có M(x) = 0
Suy ra –4x + 8 = 0
x = 2.
Vậy đa thức M(x) có nghiệm là x = 2.
Câu 14:
Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.
 Xem đáp án
Xem đáp án
Gọi số đo ba góc của tam giác đó lần lượt là x, y, z (0° < x, y, z < 180°).
Tổng số đo ba góc trong tam giác bằng 180° nên x + y + z = 180°.
Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8 nên x4=y6=z8.
Theo tính chất dãy tỉ số bằng nhau ta có:
x4=y6=z8=x+y+z4+6+8=180∘18=10∘
Suy ra x = 4.10° = 40°; y = 6.10° = 60°; z = 8.10° = 80°.
Vậy số đo ba góc của một tam giác là 40°; 60° và 80°.
Câu 15:
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể. Xem đáp án
Xem đáp án
Biến cố B là biến cố chắc chắn, biến cố C là biến cố không thể.
Câu 16:
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
 Xem đáp án
Xem đáp án
Biến cố ngẫu nhiên là biến cố A và D.
Khi gieo ngẫu nhiên xúc xắc 6 mặt cân đối thì có 6 kết quả xảy ra đối với mặt xuất hiện của con xúc xắc và 6 kết quả này có khả năng xảy ra như nhau.
Trong các số 1; 2; 3; 4; 5; 6, chỉ có 1 số lẻ và chia hết cho 3 là số 3. Vậy xác suất của biến cố A là 16.
Trong các số 1; 2; 3; 4; 5; 6, có 2 số chia cho 4 dư 1 là số 1; 5. Vậy xác suất của biến cố D là 26=13.
Câu 17:
Cho ∆ABC cân tại A có ˆA=45∘.
Tính số đo các góc của tam giác ABC từ đó so sánh các cạnh của tam giác ABC.
 Xem đáp án
Xem đáp án
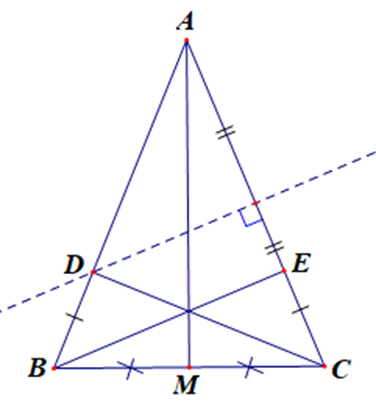
Tam giác ABC cân tại A nên AB = AC và ˆB=ˆC.
Theo định lí tổng ba góc của một tam giác ta có: ˆA+ˆB+ˆC=180∘.
Suy ra 2ˆB=180∘−ˆA=180∘−45∘=135∘.
Do đó ˆB=ˆC=67,5∘.
Vì ˆA<ˆB nên BC < AC (quan hệ giữa góc và cạnh trong tam giác).
Vậy BC < AB = AC.
Câu 18:
Cho ∆ABC cân tại A có ˆA=45∘.
Đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Chứng minh ∆BCD = ∆CBE. Từ đó suy ra ^BDC=^CEB.
 Xem đáp án
Xem đáp án
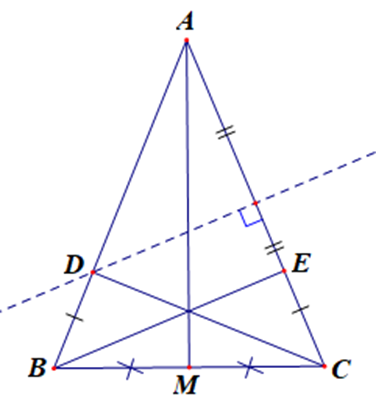
Xét ∆BCD và ∆CBE, có:
BC là cạnh chung.
CE = BD (giả thiết).
^DBC=^ECB (do ∆ABC cân tại A).
Do đó ∆BCD = ∆CBE (c.g.c)
Suy ra ^BDC=^CEB (hai góc tương ứng).
Câu 19:
Cho ∆ABC cân tại A có ˆA=45∘.
Kẻ đường trung tuyến AM của tam giác ABC. Chứng minh ba đường thẳng AM, BE, CD đồng quy tại một điểm.
 Xem đáp án
Xem đáp án
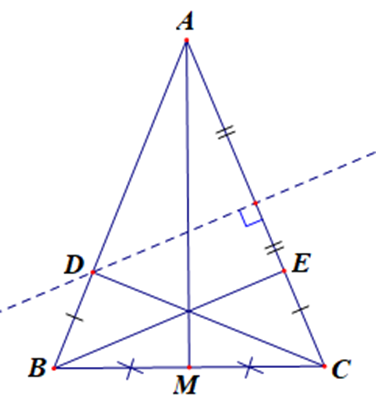
Vì điểm D thuộc đường trung trực của cạnh AC nên DA = DC.
Do đó ∆ACD cân tại D.
Suy ra ^ACD=^CAD=45∘ (tính chất tam giác cân)
∆ACD cân tại D có ^ACD=^CAD=45∘ nên ∆ACD vuông cân tại D.
Suy ra CD ⊥ AB hay ^BDC=90∘
Mà ^BDC=^CEB (câu b) nên ^CEB=90∘ hay BE ⊥ AC.
Vì ∆ABC cân tại A có AM là đường trung tuyến nên M là trung điểm BC.
Xét ∆ABM và ∆ACM, có:
AM là cạnh chung,
AB = AC (do ∆ABC cân tại A),
BM = CM (do M là trung điểm BC).
Do đó ∆ABM = ∆ACM (c.c.c).
Suy ra ^AMB=^AMC (cặp góc tương ứng).
Mà ^AMB+^AMC=180∘ (hai góc kề bù).
Suy ra ^AMB=^AMC=180∘:2=90∘.
Do đó AM ⊥ BC.
Vì vậy AM là đường cao của ∆ABC.
∆ABC có AM, BE, CD là ba đường cao, suy ra AM, BE, CD đồng quy tại một điểm, điểm đó là trực tâm của ∆ABC.
Câu 20:
Tìm số nguyên x để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1.
 Xem đáp án
Xem đáp án
Ta thực hiện đặt tính chia đa thức như sau:
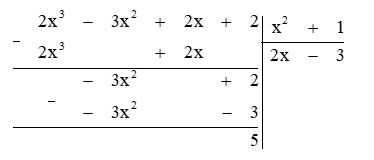
Để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1 thì 5 ⁝ (x2 + 1)
Hay (x2 + 1) ∈ Ư(5) = {–1; 1; –5; 5}.
Mà x2 + 1 ≥ 1 với mọi số nguyên x.
Do đó (x2 + 1) ∈ {1; 5}.
• Với x2 + 1 = 1 suy ra x = 0 (thỏa mãn x là số nguyên)
• Với x2 + 1 = 5
Suy ra x2 = 4
Do đó x = 2 (thỏa mãn) hoặc x = –2 (thỏa mãn)
Vậy có 3 giá trị của x thỏa mãn đề bài là x ∈ {0; –2; 2}.
