Bài tập Lượng giác từ đề thi đại học cơ bản, nâng cao có đáp án (P1)
-
247 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 9:
Cho phương trình . Có bao nhiêu giá trị nguyên của m để phương trình có đúng một nghiệm thuộc
Câu 13:
Tìm điều kiện cần và đủ của a, b, c để phương trình asinx+bcosx=c có nghiệm
 Xem đáp án
Xem đáp án
Điều kiện để phương trình asinx + bcosx = c có nghiệm là: .
Chọn D
Câu 20:
Phương trình nào dưới đây vô nghiệm:
 Xem đáp án
Xem đáp án
+) Xét phương trình: 3sinx – 2 = 0
Vì nên phương trình này có nghiệm. Do đó loại A.
+) Xét phương trình: . Do đó loại B
+) Xét phương trình: tanx = 3 (điều kiện xác định: )
. Do đó loại C
+) Xét phương trình: sinx + 3 = 0
Mà nên phương trình đã cho vô nghiệm. Do đó D đúng.
Chọn D
Câu 27:
Nghiệm âm lớn nhất của phương trình là
 Xem đáp án
Xem đáp án
Điều kiện xác định: \(cosx \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
Khi đó phương trình trở thành:
\( \Leftrightarrow \left[ \begin{array}{l}tanx = - 1\\\tan x = - \frac{3}{2}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{4} + k\pi \\x = {\rm{arctan}}\left( { - \frac{3}{2}} \right) + k\pi \end{array} \right.,k \in \mathbb{Z}\)
+) Với họ nghiệm \(x = - \frac{\pi }{4} + k\pi \), nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\) khi k = 0.
+) Với họ nghiệm \(x = {\rm{arctan}}\left( { - \frac{3}{2}} \right) + k\pi \), nghiệm âm lớn nhất là: \(x = {\rm{arctan}}\left( { - \frac{3}{2}} \right)\) khi k = 0.
Vậy nghiệm âm lớn nhất của phương trình: \(x = - \frac{\pi }{4}\).
Chọn C.
Câu 29:
Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là
 Xem đáp án
Xem đáp án
Xét phương trình: 1 + cosx + cos2x + cos3x = 0
\( \Leftrightarrow \)1 + cosx + 2cos2x – 1 + cos3x = 0
\( \Leftrightarrow \)2cos2x + cosx + cos3x = 0
\( \Leftrightarrow \)2cos2x + 2cos2xcosx = 0
\( \Leftrightarrow \)2cosx(cosx + cos2x) = 0
\( \Leftrightarrow 4cosx.cos\frac{{3x}}{2}{\rm{. }}cos\frac{x}{2} = {\rm{ }}0\)
\( \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\cos\frac{{3x}}{2} = 0\\cos\frac{x}{2} = {\rm{ }}0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k\pi \\x = \frac{\pi }{3} + k\frac{{2\pi }}{3}\\x = {\rm{ }}\pi + {\rm{k2}}\pi \end{array} \right.,k \in \mathbb{Z}\)
Điểm A và B biểu diễn nghiệm \(x = \frac{\pi }{2} + k\pi \) trên đường tròn lượng giác.
Điểm C biểu diễn nghiệm \(x = \pi + k2\pi \) trên đường tròn lượng giác.
Điểm D, C và E biểu diễn nghiệm \(x = \frac{\pi }{3} + k\frac{{2\pi }}{3}\) trên đường tròn lượng giác.
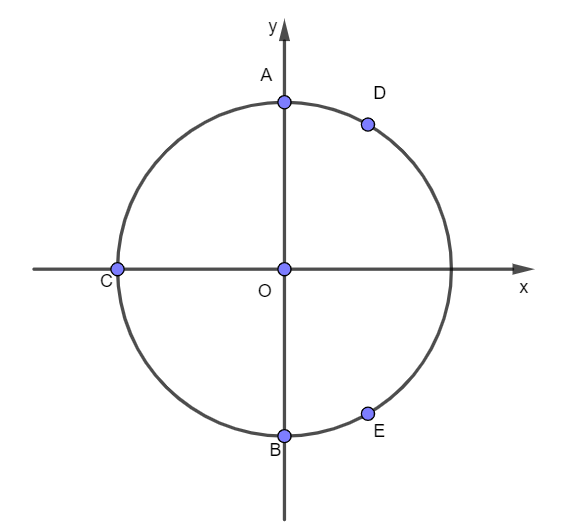
Có tất cả 5 điểm biểu diễn các nghiệm của phương trình đã cho.
