16 câu hỏi trắc nghiệm thuộc Dạng 2: Dựng thiết diện song song với một đường thẳng có đáp án

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là tâm hình bình hành ABCD. M là trung điểm của SB. Tìm thiết diện của mặt phẳng

(α)

với hình chóp S.ABCD nếu

(α)

đi qua M; song song với SD và CD.

Xem đáp án

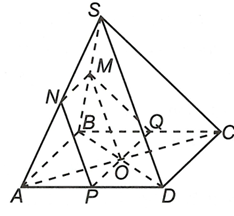
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là tâm hình bình hành ABCD. M là trung điểm của SB (ảnh 1)

Ta có $M \in (α)$ và $M \in (S A B) .$

Mặt khác $C D // (α)$ suy ra $(α) \cap (S A B) = M x$ trong đó $M x // C D$ và $M x \cap S A = \{N\} .$

Ta lại có MO là đường trung bình của tam giác SBD nên $MO // S D \Rightarrow O \in (α) .$

Suy ra $(α) \cap (A B C D) = O y, Oy // C D$ và Oy cắt AD và BC lần lượt tại P, Q.

Vậy MNPQ là thiết diện của mặt phẳng

(α)

với hình chóp S.ABCD.

Câu 2:

Cho tứ diện ABCD. Trên các cạnh BC, CD, AD lấy các điểm M, N, P lần lượt là trung điểm của chúng. Dựng thiết diện của ABCD với mặt phẳng

Xem đáp án

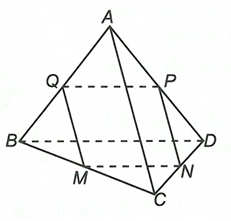
Cho tứ diện ABCD. Trên các cạnh BC, CD, AD lấy các điểm M, N, P lần lượt là trung điểm của chúng. (ảnh 1)

Ta có MN là đường trung bình của tam giác BCD nên MN // BD

Do $P \in A D$ nên $(M N P) \cap (A B D) = P x$ sao cho $P x // B D$ và $P x \cap A B = \{Q\} .$

Khi đó thiết diện của mặt phẳng (MNP) với tứ diện ABCD là tứ giác MNPQ.

Câu 3:

Cho hình chóp S.ABCD có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N lần lượt là trung điểm của các cạnh SB và SC.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

Xem đáp án

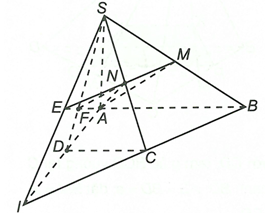
a) Ta có S là điểm chung thứ nhất của hai mặt phẳng (SAD) và (SBC)

Kéo dài BC cắt AD tại I. Khi đó I là điểm chung thứ hai của hai mặt phẳng (SAD) và (SBC)

Suy ra SI là giao tuyến của hai mặt phẳng (SAD) và (SBC)

Câu 4:

b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)

Xem đáp án

b) Trong mặt phẳng (SBC) kéo dài MN cắt SI tại E.

Gọi F là giao điểm của AE và SD

Ta có $F \in S D$ và $F \in A E$ mà $A E \subset (A M N)$ nên $\{F\} = S D \cap (A M N)$

Câu 5:

c) Dựng thiết diện của hình chóp với mặt phẳng (AMN)

Xem đáp án

c) Ta có $M N // B C$ nên $B C // (A M N)$

Thiết diện (AMN) với hình chóp S.ABCD là tứ giác AMNF.

Câu 6:

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi H và K lần lượt là trung điểm các cạnh CB và CD, M là điểm bất kì trên cạnh SA. Dựng thiết diện của hình chóp với mặt phẳng (MHK)

Xem đáp án

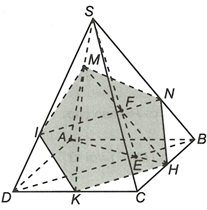
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi H và K lần lượt là trung điểm các cạnh CB và CD, M là điểm bất kì trên cạnh SA (ảnh 1)

Ta có HK là đường trung bình của tam giác BCD nên HK // BD

Gọi $\{E\} = A H \cap B D;$ nối SE cắt MH tại F. Do HK // BD nên giao tuyến của (MHK) với mặt phẳng (SBD) là đường thẳng đi qua F và song song với BD cắt SB, SD lần lượt tại N, I.

Suy ra thiết diện của (MHK) với hình chóp S.ABCD là ngũ giác MNHKI

Câu 7:

Cho tứ diện ABCD. Gọi I, J, K lần lượt là trọng tâm của các tam giác BCD, CDA, ABC. Dựng thiết diện của ABCD với mặt phẳng (IJK)

Xem đáp án

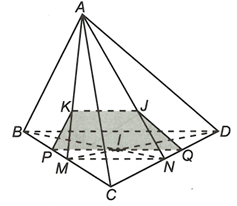
Cho tứ diện ABCD. Gọi I, J, K lần lượt là trọng tâm của các tam giác BCD, CDA, ABC. Dựng thiết diện của ABCD với mặt phẳng (IJK) (ảnh 1)

Gọi M và N lần lượt là trung điểm của BC và CD.

Do K, J lần lượt là trọng tâm của tam giác ABC và ACD nên $\frac{A K}{A M} = \frac{A J}{A N} = \frac{2}{3} .$

Áp dụng định lý Ta-lét suy ra KJ // MN

Suy ra $(K I J) \cap (B C D) = I x,$ trong đó $I x // M N .$

Giả sử Ix cắt BC, CD lần lượt tại P và Q. Vậy thiết diện của mặt phẳng (KIJ) với tứ diện ABCD là tứ giác KPQJ.

Câu 8:

Cho tứ diện ABCD có AB vuông góc với CD, tam giác BCD vuông tại C và góc $\hat{B D C} = 30 ° .$ M là một điểm thay đổi trên cạnh BD; $A B = B D = a;$ đặt $B M = x .$ Mặt phẳng $(α)$ đi qua M và song song với AB, CD.

a) Dựng thiết diện của tứ diện với $(α)$

Xem đáp án

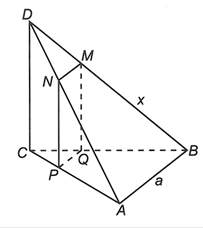
Cho tứ diện ABCD có AB vuông góc với CD, tam giác BCD vuông tại C và góc BDC = 30 độ. a) Dựng thiết diện của tứ diện với (anpha) (ảnh 1)

a) Qua M dựng đường thẳng song song với AB cắt AD tại N.

Qua M, N dựng các đường thẳng song song với CD cắt BC, AC lần lượt tại Q, P. Tứ giác MNPQ là thiết diện tạo bởi mặt phẳng $(α)$ với tứ diện ABCD.

Câu 9:

b) Tính diện tích S của thiết diện.

Xem đáp án

b) Theo cách dựng trên ta có NP // MQ

Mặt khác AB // (MNPQ) mà AB và PQ cùng nằm trên mặt phẳng (ABC) nên AB // PQ.

Suy ra PQ // MN hay tứ giác MNPQ là hình bình hành.

Ta lại có $C D ⊥ A B \Rightarrow M N ⊥ N P .$ Vậy MNPQ là hình chữ nhật.

Xét tam giác BCD, có $C D = B D . \cos \hat{B D C} = a . \cos 30 ° = \frac{a \sqrt{3}}{2} .$

Do $M Q // C D$ suy ra $\frac{B M}{B D} = \frac{M Q}{C D} \Rightarrow M Q = \frac{B M}{B D} . C D = \frac{x}{a} . \frac{a \sqrt{3}}{2} = \frac{x \sqrt{3}}{2} .$

Ta cũng có $\frac{D M}{D B} = \frac{M N}{A B} \Rightarrow M N = \frac{D M}{D B} . A B = D M = a - x .$

Vậy diện tích của thiết diện MNPQ là $S = M N . M Q = (a - x) \frac{x \sqrt{3}}{2} .$

Câu 10:

c) Xác định vị trí của M trên BD để S lớn nhất.

Xem đáp án

c) Áp dụng bất đẳng thức Cauchy cho hai số dương $a - x$ và x.

Ta có $a = a - x + x \geq 2 \sqrt{(a - x) x} \Rightarrow (a - x) x \leq \frac{a^{2}}{4} .$

Suy ra $S \leq \frac{a^{2}}{4} . \frac{\sqrt{3}}{2} = \frac{a^{2} \sqrt{3}}{8} .$ Dấu “=” xảy ra khi và chỉ khi $a - x = x \Leftrightarrow x = \frac{a}{2}$ hay M là trung điểm của BD.

Vậy diện tích của thiết diện lớn nhất khi M là trung điểm của BD.

Câu 11:

Cho tứ diện ABCD, điểm M thuộc đoạn AC. Mặt phẳng

(α)

qua M song song với AB và AD. Thiết diện của

(α)

với tứ diện ABCD là hình gì?

A. Hình tam giác

B. Hình bình hành

C. Hình thang

D. Hình ngũ giác

Xem đáp án

Đáp án A

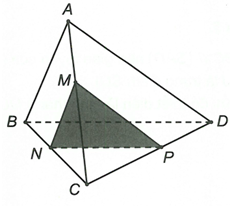
Cho tứ diện ABCD, điểm M thuộc đoạn AC. Mặt phẳng (anpha) qua M song song với AB và AD. (ảnh 1)

$(α)$ và $(A B C)$ có M chung, $(α)$ song song với AB, $A B \subset (A B C)$

$\Rightarrow (α) \cap (A B C) = M x, M x // A B$ gọi $M x \cap B C = \{N\} .$

$(α)$ và có M chung, $(α)$ song song với AD, $A D \subset (A C D)$

$\Rightarrow (α) \cap (A C D) = M y, M y // A D$ và $M y \cap C D = \{P\} .$

Ta có $(α) \cap (A B C) = M N; (α) \cap (A C D) = M P; (α) \cap (B C D) = N P .$

Thiết diện của

(α)

với tứ diện ABCD là tam giác MNP

Câu 12:

Cho tứ diện ABCD, điểm G là trọng tâm tam giác BCD. Mặt phẳng

(α)

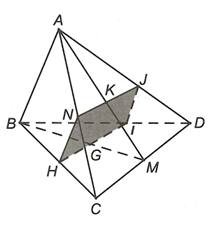
qua G, song song với AB và CD.

(α)

cắt trung tuyến AM của tam giác ACD tại K. Chọn khẳng định đúng.

A.

(α)

cắt tứ diện ABCD theo thiết diện là một hình tam giác

B.

A K = \frac{2}{3} A M .

C.

A K = \frac{1}{3} A M .

D. Giao tuyến của

(α)

và

(C B D)

cắt CD

Xem đáp án

Đáp án B

Cho tứ diện ABCD, điểm G là trọng tâm tam giác BCD. Mặt phẳng qua G, song song với AB và CD. (ảnh 1)

$(α)$ qua G, song song với CD $\Rightarrow (α) \cap (B C D) = H I$ (giao tuyến đi qua G và song song CD, $H \in B C, I \in C D$ ).

Tương tự ta được $(α) \cap (A B D) = I J$ sao cho $I J // A B .$

$(α) \cap (A C D) = J N$ sao cho $J N // C D .$

$(α) \cap (A B C) = H N .$

Vậy $(α)$ là $(H N J I)$

Vì G là trọng tâm tam giác BCD mà $I G // C D$ nên $\frac{B G}{B M} = \frac{B I}{B C} = \frac{2}{3} .$

Mặt khác IJ song song AB nên $\frac{B I}{B C} = \frac{A J}{A D} = \frac{2}{3} .$

Lại có JK song song DM (vì $K \in A M, M \in C D$ ) nên $\frac{A K}{A M} = \frac{A J}{A D} = \frac{2}{3} .$

Vậy $A K = \frac{2}{3} A M .$

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) qua BD và song song với SA. Khi đó mặt phẳng (P) cắt hình chóp S.ABCD theo thiết diện là một

A. hình thang

B. hình chữ nhật

C. hình bình hành

D. tam giác

Xem đáp án

Đáp án D

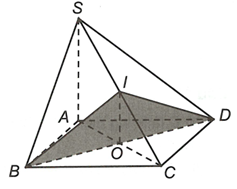
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) qua BD và song song với SA (ảnh 1)

Gọi O là giao điểm của hai đường chéo AC và BD => I là trung điểm của AC và BD.

$\{\begin{cases} (P) // S A \\ B D \subset (P) \end{cases} \Rightarrow (P) \cap (S A C) = O I .$

Khi đó $O I // S A$ và I là trung điểm của SC. $(P) \cap (S B C) = B I$ và $(P) \cap (S C D) = I D .$

Vậy thiết diện là tam giác BDI.

Câu 14:

Cho hình chóp S.ABCD, gọi M là trung điểm AB, mặt phẳng

(α)

qua M song song với SB và AD, thiết diện của hình chóp cắt bởi

(α)

là hình gì?

A. Hình bình hành

B. Hình thang

C. Tứ giác

D. Ngũ giác.

Xem đáp án

Đáp án B

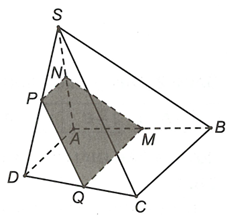
Cho hình chóp S.ABCD, gọi M là trung điểm AB, mặt phẳng anpha qua M song song với SB và AD, (ảnh 1)

$(α)$ song song với SB nên $(α)$ cắt $(S A B)$ theo giao tuyến MN với N là trung điểm SA.

$(α)$ song song với AD nên $(α)$ cắt $(A B C D)$ và $(S A D)$ theo giao tuyến MQ và NP với P, Q là trung điểm của SD và $M Q // A D .$

Ta được thiết diện là hình thang MNPQ.

Câu 15:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng

(I B C)

là

A. tam giác IBC

B. hình thang IJBC (J là trung điểm SD)

C. hình thang IGBC (G là trung điểm của SB)

D. tứ giác IBCD

Xem đáp án

Đáp án B

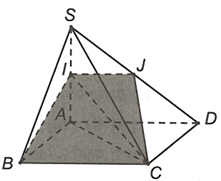
: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA. Thiết diện của hình chóp S.ABCD (ảnh 1)

$B C // (S A D)$ nên giao tuyến của $(I B C)$ và $(S A D)$ là IJ (J là trung điểm SD).

Khi đó thiết diện là hình thang IJCB.

Câu 16:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc đoạn SB (M không trùng với S và B). Mặt phẳng

(A D M)

cắt hình chóp S.ABCD theo thiết diện là

A. hình bình hành

B. tam giác

C. hình chữ nhật

D. hình thang

Xem đáp án

Đáp án D

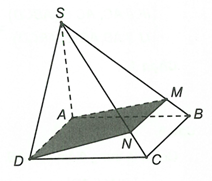
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc đoạn SB (M không trùng với S và B). (ảnh 1)

Ta có M là một điểm thuộc đoạn SB với M khác S và B.

Suy ra $\{\begin{cases} M \in (A D M) \cap (S B C) \\ A D \subset (A D M) \\ B C \subset (S B C) \\ A D // B C \end{cases}$

$\Rightarrow (A D M) \cap (S B C) = M x$ sao cho $M x // B C // A D .$

Gọi $\{N\} = M x \cap S C$ thì $(A D M)$ cắt hình chóp S.ABCD theo thiết diện là tứ giác AMND. Vì $M N // A D$ và MN với AD không bằng nhau nên tứ giác AMND là hình thang.

Bài tập chuyên đề toán 11 Bài 3: Đường thẳng song song với mặt phẳng có đáp án

Dạng 2: Dựng thiết diện song song với một đường thẳng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương